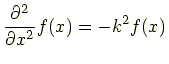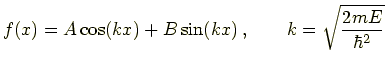定常状態のシュレディンガー方程式を解く

では常微分方程式 (7.10) を解いてゆこう．ポテンシャル $V(x)$ は

$$V(x)=\begin{cases}0 & (-L \le x \le L) \\ \infty & (x>-L,~ L<x) \end{cases}$$

で定義されていた．$V(x)=0$ の場合は

$$\left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + 0\right)f(x) = Ef(x)$$

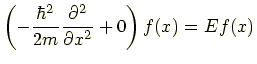つまり

$$-\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} f(x) = Ef(x)$$

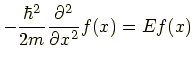となることがすぐにわかる．だが $V(x)=\infty$ の場合は

$$\Bigl(-\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + \infty \Bigr) f(x) = Ef(x)$$

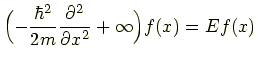となってよくわからない．この場合，つまり $x>-L,~ L<x$ の場合は粒子が存在できない，すなわち

$$f(x) = 0$$

である考える．したがって

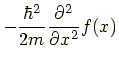$$-\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} f(x) = Ef(x) \qquad (-L \le x \le L)$$ (7.12)

$$f(x) = 0 \qquad (x > -L,~ L < x)$$ (7.13)

の2つの場合に分けられる．式 (7.12) より

$$\frac{\partial^2}{\partial x^2} f(x) = -\frac{2mE}{\hbar^2} f(x)$$

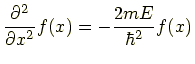ここで $$k=\sqrt{\frac{2mE}{\hbar^2}}$$ とおくと，

$$\frac{\partial^2}{\partial x^2} f(x) = -k^2 f(x)$$

となる．式 (7.8.4) に解として

$$f(x) = e^{\alpha x}$$

を代入すると

$$(\alpha ^2 + k^2) = 0$$ (7.14)

$$\therefore\qquad \alpha = \pm ik$$ (7.15)

よって特解は

$$e^{ikx},~ e^{-ikx}$$ (7.16)

一般解は三角関数の線型結合で書けて

$$f(x) = A\cos (kx) + B \sin (kx)\, , \qquad k=\sqrt{\frac{2mE}{\hbar^2}}$$ (7.17)

となる．