物理量と演算子

古典力学におけるハミルトニアン

$$H(p,q) = E$$

において

$$p \rightarrow \frac{\hbar}{i}\frac{\partial}{\partial q}$$

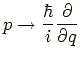という演算子(operator)と置いたもの

$$\left\{H\left(\frac{\hbar}{i}\frac{\partial}{\partial q},q\right)-E\right\}\psi = 0$$

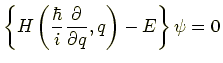でシュレディンガー方程式が得られる．これをハミルトニアン演算子 という．また，$E$ については

$$E \rightarrow -\frac{\hbar}{i}\frac{\partial}{\partial t}$$

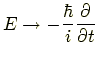という演算子に置きかえる．ゆえにシュレディンガー方程式は

$$\left\{H\left(\frac{\hbar}{i}\frac{\partial}{\partial q},q\right) +\frac{\hbar}{i}\frac{\partial}{\partial t}\right\}\psi = 0$$

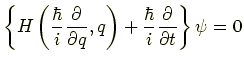となる．

ポテンシャル $V(x,y,z)$ のなかを運動する質量 $m$ の粒子のハミルトニアンは

$$H = \frac{1}{2m}\left(p_x^2+p_y^2+p_z^2\right) + V(x,y,z)$$

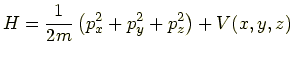であるから，これを演算子

$$p_x \rightarrow \frac{\hbar}{i}\frac{\partial}{\partial x}~, \qqu... ...\partial y}~, \qquad p_z \rightarrow \frac{\hbar}{i}\frac{\partial}{\partial z}$$

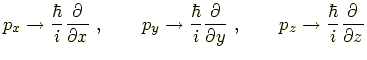に置きかえると，ハミルトニアン演算子は

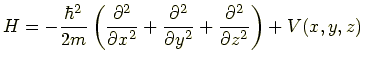$$H = -\frac{\hbar^2}{2m}\left(\frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\right) + V(x,y,z)$$ (7.3)

となる．したがって，この場合のシュレディンガー方程式は

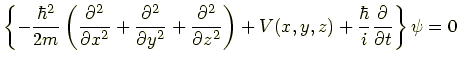$$\left\{-\frac{\hbar^2}{2m}\left(\frac{\partial^2}{\partial x^2} +... ...^2}\right) +V(x,y,z)+\frac{\hbar}{i}\frac{\partial}{\partial t} \right\}\psi =0$$ (7.4)

である．

量子力学では運動量 $p$ と運動量演算子 $\frac{\hbar}{i}\frac{\partial}{\partial q}$ をあまり区別しない． 演算子であることを明確にするためには上に $\wedge$ を付けて $\hat{p}$ と書く． 演算子で与えられる量（運動量，ハミルトニアン等）をq-数（きゅーすう）， 固有値など演算子でない量をc-数（しーすう）と呼ぶ．