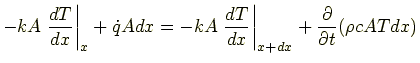1次元熱伝導方程式

熱伝導の一般化を考える．断面積 $A$，厚さ $dx$ の要素の左面から $q_x$ の熱量が流入し， 右面から $q_{x+dx}$ の熱量が流出するとする．このとき考えられる量は

• 左面から流入する熱量： $q_x$
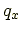
• 要素内で発生した熱量： $q_\mathrm{gen}$
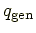
• 右面から流出する熱量： $q_{x+dx}$
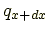
• 要素内のエネルギー変化： $\frac{\partial E}{\partial t}$

であるから，この要素内でのエネルギー収支は

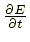
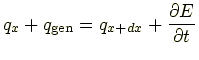$$q_x+q_\mathrm{gen}=q_{x+dx}+\frac{\partial E}{\partial t}$$ (4.4)

と表される．単位時間あたりの発熱量を $dq/dt=\dot{q}$，要素の比熱を $c$，要素の密度を $\rho$ とすると

$$\qquad q_x =-kA\left.\frac{dT}{dx}\right\vert _x$$

$$\qquad q_{\mathrm{gen}} =\dot{q}Adx$$

$$\qquad q_{x+dx} =-kA\left.\frac{dT}{dx}\right\vert _{x+dx}$$

$$\qquad \frac{\partial E}{\partial t} =\frac{\partial}{\partial t}(\rho cATdx)$$

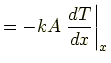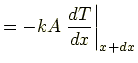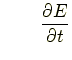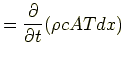であるから，エネルギー収支はつぎのようになる．

$$-kA\left.\frac{dT}{dx}\right\vert _x + \dot{q}Adx = -kA\left.\frac{dT}{dx}\right\vert _{x+dx} + \frac{\partial}{\partial t}(\rho cATdx)$$ (4.5)

ここで，テイラー展開 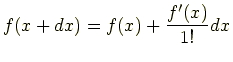$$f(x+dx)=f(x)+\frac{f'(x)}{1!}dx$$ より

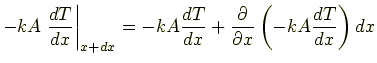$$-kA\left.\frac{dT}{dx}\right\vert _{x+dx} =-kA\frac{dT}{dx}+\frac{\partial}{\partial x}\left(-kA\frac{dT}{dx}\right)dx$$ (4.6)

これを式(4.5)に代入すると

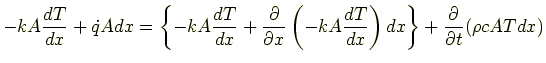$$-kA\frac{dT}{dx} + \dot{q}Adx = \left\{-kA\frac{dT}{dx}+\frac{\pa... ...eft(-kA\frac{dT}{dx}\right)dx\right\} + \frac{\partial}{\partial t}(\rho cATdx)$$ (4.7)

整理して

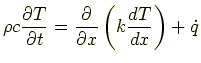$$\rho c\frac{\partial T}{\partial t}=\frac{\partial}{\partial x}\left(k\frac{dT}{dx}\right)+\dot{q}$$ (4.8)

が得られる．これを1次元熱伝導方程式 （one dimential equation of heat conduction）という． この方程式によって様々な初期条件，境界条件下で，要素内の温度分布と温度変化を予測することができる．