p-ベクトルの内積
私達は,外積空間 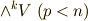 が,各
が,各 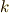 に応じてそれぞれベクトル空間になっていることを知っています.その元のことを,次数を冠してk-ベクトルのように呼ぶのでした.私達の外積代数には,
に応じてそれぞれベクトル空間になっていることを知っています.その元のことを,次数を冠してk-ベクトルのように呼ぶのでした.私達の外積代数には, 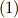 加法,
加法, 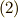 スカラー積,そして当然
スカラー積,そして当然 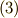 外積(ウェッジ積)という演算が入っています.今のところ知っているのは,これだけですね.
外積(ウェッジ積)という演算が入っています.今のところ知っているのは,これだけですね.
しかし,思い起こせば, 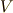 には自然に内積という演算が入っていました.
には自然に内積という演算が入っていました. 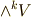 にも内積は入れられないものでしょうか.これは,もちろん,拡張された一般的な内積という意味で,高校で習うベクトルの内積とは異なるものになるはずです.一般の内積について,よく分からない人は,まず 内積空間 を復習すると良いと思います.
にも内積は入れられないものでしょうか.これは,もちろん,拡張された一般的な内積という意味で,高校で習うベクトルの内積とは異なるものになるはずです.一般の内積について,よく分からない人は,まず 内積空間 を復習すると良いと思います.
| [*] | 内積は演算というよりはむしろ,二つの元をスカラーに対応させる写像で,線形汎関数を作用させると考えた方が正確かも知れません.何にせよ,内積を考えたい主な動機は,内積を入れることで空間に距離(ノルム)や角度の概念を導入することが出来ることと,内積を入れることで最低限,直交という概念を導入できることです.距離と直交という概念を使ってはじめて,正規直交基底という基底の組を考えることも出来るようになります. |
p-ベクトルの内積
まず, 内積空間 の記事に書いた,内積の定義を再掲します.これらの性質を満たす演算一般を内積と呼ぶということでした.抽象的な議論に慣れていない人は,これらが幾何ベクトルの内積よりも一般的な定義になっていることに注意して下さい.
【内積の定義】
- 線形性がある.
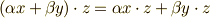
- 対称性がある.
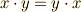
- 正定値性がある.
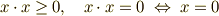
逆に言えば, 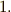 〜
〜 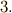 を満たす演算が何か定義できれば,それを堂々と内積と呼んでも良いわけです.(ただし,性質
を満たす演算が何か定義できれば,それを堂々と内積と呼んでも良いわけです.(ただし,性質  は,後で少し条件を緩めます.その理由も述べます.)
は,後で少し条件を緩めます.その理由も述べます.)
さて,こんなことを念頭に置きつつ, 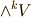 に属する二つの元,
に属する二つの元, 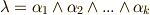 と
と 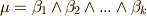 の内積を,次のような行列式で定義することにします.ただし Vには内積が定義されているとします .
の内積を,次のような行列式で定義することにします.ただし Vには内積が定義されているとします .
| [†] | 今後, 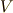 として考えるベクトル空間は,ユークリッド空間 として考えるベクトル空間は,ユークリッド空間 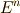 かミンコフスキー空間 かミンコフスキー空間 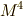 で,どちらにも内積は定義できますので,『 で,どちらにも内積は定義できますので,『 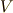 に内積を定義できるのか』をあまり心配する必要はありません.ただし,ミンコフスキー空間には内積が負になる基底があり,そのため,この後の議論には に内積を定義できるのか』をあまり心配する必要はありません.ただし,ミンコフスキー空間には内積が負になる基底があり,そのため,この後の議論には 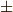 という記号が何度も出てきます.『自分にはユークリッド空間しか関係ない』という人は, という記号が何度も出てきます.『自分にはユークリッド空間しか関係ない』という人は,  の方だけ考えるようにして下さい. の方だけ考えるようにして下さい. |
![(\lambda, \mu ) &= {\rm det}[(\alpha_{i} , \beta_{j})] \\& = \left| \begin{array}{cccc}(\alpha_{1} , \beta_{2}) & (\alpha_{1} , \beta_{2}) & \cdots & (\alpha_{1} , \beta_{k}) \\(\alpha_{2} , \beta_{1}) & (\alpha_{2} , \beta_{2}) & \cdots & \vdots \\\vdots & \vdots & \ddots & \vdots \\(\alpha_{k} , \beta_{1}) & \cdots & \cdots & (\alpha_{k} , \beta_{k}) \\ \end{array} \right| \tag{1}](./c1b74331067cb9ba7fb1c24ac0746324.png)
行列の各成分は, 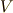 上の普通の内積になっています.この行列式が,先ほどの内積の性質を満たしているかを実際に確認してみましょう(多少,線形代数の知識が必要かも知れません).まず,内積の性質
上の普通の内積になっています.この行列式が,先ほどの内積の性質を満たしているかを実際に確認してみましょう(多少,線形代数の知識が必要かも知れません).まず,内積の性質 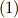 が満たされることは,行列式が一般に
が満たされることは,行列式が一般に  を満たすことから明らかです.(これを,行列式の多重線形性と呼びます.ここでは,あまり詳しく説明できないので,ピンと来ない人は線形代数の教科書を調べてみて下さい.)
を満たすことから明らかです.(これを,行列式の多重線形性と呼びます.ここでは,あまり詳しく説明できないので,ピンと来ない人は線形代数の教科書を調べてみて下さい.)
内積の性質 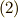 も,
も, 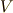 のベクトルの内積について
のベクトルの内積について 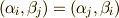 が成り立つことから明らかでしょう. (式
が成り立つことから明らかでしょう. (式 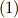 の形から,転置行列の性質
の形から,転置行列の性質 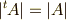 を使って示せばもっとエレガントです.)
を使って示せばもっとエレガントです.)
性質 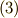 についてですが,式
についてですが,式 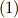 の行列式が常に正定値を取るとは限りません.そこで,ここでは正定値という条件を少し緩め, 非退化であれば良い とします.これを 拡張された内積の定義 とします.非退化とはどういうことかと言うと,『内積
の行列式が常に正定値を取るとは限りません.そこで,ここでは正定値という条件を少し緩め, 非退化であれば良い とします.これを 拡張された内積の定義 とします.非退化とはどういうことかと言うと,『内積 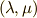 で
で 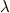 を固定し,
を固定し, 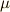 の方を次々と変化させるときに,常に
の方を次々と変化させるときに,常に 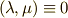 を満たすのは
を満たすのは 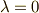 の場合しかない』という性質のことです.式
の場合しかない』という性質のことです.式 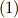 で定義される量が,非退化性を持つことも明らかでしょう.なぜ,いきなり内積の条件を緩めたのかを知りたい人は,次の註を読んでください.
で定義される量が,非退化性を持つことも明らかでしょう.なぜ,いきなり内積の条件を緩めたのかを知りたい人は,次の註を読んでください.
| [‡] | このように正定値性を緩めた内積を,不定値内積と呼びます.なぜ,このような定義の拡張をしておくのか,その背後にある野望を少し説明しておきましょう.内積を導入すると,空間に距離の概念を入れることが出来ます.例えば,  のように のように  のノルムを決めることが出来ます.内積とはベクトル空間の直積空間からスカラーへの写像だと見ることが出来ましたが,このようにベクトルの大きさを正数に写像するというのは,『距離 のノルムを決めることが出来ます.内積とはベクトル空間の直積空間からスカラーへの写像だと見ることが出来ましたが,このようにベクトルの大きさを正数に写像するというのは,『距離 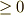 』と考える立場です.普通は,これであまり困ることは無いわけですが,実は,ミンコフスキー空間と呼ばれる,相対性理論で使われる空間に,外積代数(を応用した微分形式というもの)を使いたいという野望があるのです.ミンコフスキー空間は,後で説明するように,三次元の空間に時間軸を合わせた四次元空間 』と考える立場です.普通は,これであまり困ることは無いわけですが,実は,ミンコフスキー空間と呼ばれる,相対性理論で使われる空間に,外積代数(を応用した微分形式というもの)を使いたいという野望があるのです.ミンコフスキー空間は,後で説明するように,三次元の空間に時間軸を合わせた四次元空間 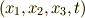 ですが,時間軸の基底ベクトル ですが,時間軸の基底ベクトル 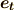 について について 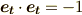 のように大きさが のように大きさが 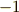 になるのです. になるのです. |
| [§] | 上の註で書いたことは,『今後は,ノルムが必ずしも正でなくとも良いとする』という立場の表明です.ノルムが負になるものを擬ノルムと呼びますが,後で触れるように,ミンコフスキー空間の時間軸は擬ノルムの例です. |
マイナスの記号に少し慣れないかも知れませんが,拡張された内積の定義を使って, 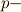 ベクトルの正規直交基底
ベクトルの正規直交基底 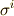 は,次式を満たすものと定めます.
は,次式を満たすものと定めます.
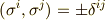
右辺の 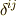 はクロネッカーのデルタです.正規直交基底の内積が負になる有名な例は,相対性理論に出て来るミンコフスキー空間です.ミンコフスキー空間は,三次元のユークリッド空間
はクロネッカーのデルタです.正規直交基底の内積が負になる有名な例は,相対性理論に出て来るミンコフスキー空間です.ミンコフスキー空間は,三次元のユークリッド空間 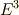 に,時間軸
に,時間軸 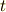 を足した四次元空間ですが,ミンコフスキー空間上の計量(微小な距離)
を足した四次元空間ですが,ミンコフスキー空間上の計量(微小な距離) 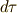 は次のように決められます.
は次のように決められます.
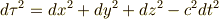
最初の  は普通の三次元ユークリッド空間
は普通の三次元ユークリッド空間 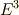 です.定数
です.定数  (光速)は形式的には無くても良いのですが,一応つけておきます.
(光速)は形式的には無くても良いのですが,一応つけておきます. 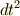 の前にマイナスが付いている点に着目して下さい.多くの人は,何となく『距離の二乗は正だ』という予見にとらわれていると思いますが,ミンコフスキー空間では 距離の定義の仕方そのものが違う ようです.時間軸の単位基底を
の前にマイナスが付いている点に着目して下さい.多くの人は,何となく『距離の二乗は正だ』という予見にとらわれていると思いますが,ミンコフスキー空間では 距離の定義の仕方そのものが違う ようです.時間軸の単位基底を 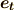 と書けば,
と書けば, 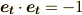 となります.本稿では,これ以上詳しくミンコフスキー空間の話はしませんが,内積の正定値性を崩し,不定値内積とした理由を察して貰えれば十分だと思います.
となります.本稿では,これ以上詳しくミンコフスキー空間の話はしませんが,内積の正定値性を崩し,不定値内積とした理由を察して貰えれば十分だと思います.
| [¶] | ミンコフスキー空間では,距離がマイナスという場合がある訳ですが,これはつまり,『 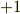 進んでから, 進んでから, 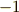 進んだ場所』というのが,数直線上を行って帰って来る以外にもあり得るということです.つまり,距離が 進んだ場所』というのが,数直線上を行って帰って来る以外にもあり得るということです.つまり,距離が  の場所が原点以外にも存在することになります.これが,具体的には『光速で移動する座標系では年をとらない』という現象に対応することになります. の場所が原点以外にも存在することになります.これが,具体的には『光速で移動する座標系では年をとらない』という現象に対応することになります. |
ここまでで,式 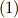 で定義した『
で定義した『 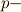 ベクトルの内積』が,確かに拡張された意味での内積の定義を満たしていることが分かりました. 外積空間も内積空間になります .(←こう書くと,なんだか違和感のる字面ですね^^ )
ベクトルの内積』が,確かに拡張された意味での内積の定義を満たしていることが分かりました. 外積空間も内積空間になります .(←こう書くと,なんだか違和感のる字面ですね^^ )
| [#] | 内積は 内積と双対空間 で紹介したように,双線形関数だと考えることも出来ます.内積を写像だと考えれば,内積の作用は,ベクトルとその双対ベクトルをセットにして,スカラーに対応させてしまうという写像だということになります.先ほど,内積の定義を少し緩めましたが,写像としてのこのような性質を,式 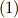 は十分に満たしています.実は, は十分に満たしています.実は, 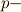 ベクトルに内積を考えた当面の理由は,次に述べる ホッジ作用素 という作用素を考えたいためで,この作用素は今後の議論に非常に重要な役割を果たします.そして,外積代数の(そして微分形式の)世界をますます美しく彩る作用素となります.もはや,その美しさは芸術の域に達しております. ベクトルに内積を考えた当面の理由は,次に述べる ホッジ作用素 という作用素を考えたいためで,この作用素は今後の議論に非常に重要な役割を果たします.そして,外積代数の(そして微分形式の)世界をますます美しく彩る作用素となります.もはや,その美しさは芸術の域に達しております. |
外積代数の正規直交基底
さきほどのように,行列式の形で内積を定義したままでは,ベクトル空間としての外積空間の基底の内積が,どうなっているのか分かりにくいと思います.内積によってベクトル空間には直交という概念が入りますから(内積の定義されたベクトル空間を計量ベクトル空間と呼ぶのでした),先ほど定義した内積によって,  を満たすような正規直交基底の組
を満たすような正規直交基底の組 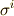 を選べるはずですが,式
を選べるはずですが,式 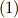 のように定義した内積が,本当に直交条件を満たすのかどうか,確認してみましょう.
のように定義した内積が,本当に直交条件を満たすのかどうか,確認してみましょう.
まず 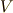 の正規直交基底を
の正規直交基底を 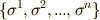 とします.(
とします.( 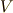 には内積が定義されているので,正規直交基底が存在するという前提からです.)このとき,
には内積が定義されているので,正規直交基底が存在するという前提からです.)このとき, 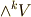 の基底は
の基底は 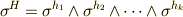 の形で表わされます.ただし,ここで
の形で表わされます.ただし,ここで 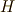 は
は 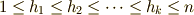 からなる整数の集合
からなる整数の集合  とします.
とします.
| [♠] | 基底の添え字を式で書くと少し面倒ですが, 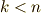 という条件から,このように書くしかないのです.そんなに大したことを言っているのではありません. という条件から,このように書くしかないのです.そんなに大したことを言っているのではありません. |
ここで, 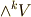 の基底
の基底 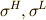 を式
を式 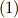 に代入すると,次のようになります.(
に代入すると,次のようになります.(  ,
, 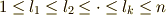 としています.)
としています.)
![(\sigma^{H}, \sigma^{L}) = {\rm det}[(\sigma^{h_{i}},\sigma^{l_{j}})]](./650a3a2e673bd12860b96b24bbc5cef3.png)
右辺の行列の成分を見てみると, 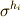 や
や 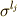 はそれぞれ
はそれぞれ 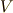 の正規直交基底ですので,もし
の正規直交基底ですので,もし  でなければ,直交条件によって行列式は
でなければ,直交条件によって行列式は  になってしまいます.逆に,もし
になってしまいます.逆に,もし  ならば,行列式の対角要素は直交条件より
ならば,行列式の対角要素は直交条件より 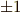 で,非対角要素は
で,非対角要素は  ですので,
ですので, 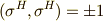 が言えます.式
が言えます.式 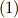 の定義による内積は,たしかに外積代数の正規直交基底の直交条件を上手く与える定義になっていることが確認できました.
の定義による内積は,たしかに外積代数の正規直交基底の直交条件を上手く与える定義になっていることが確認できました.
theorem
式 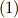 で定義される内積により,外積代数
で定義される内積により,外積代数 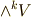 の正規直交基底
の正規直交基底 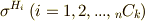 は,直交条件
は,直交条件 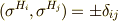 を満たします.
を満たします.
ひとつの定理
後で, ホッジのスター作用素 の記事で使いたいので,ここで内積に関する定理を一つ示しておきます.ここまでの議論とこの定理は直接は関係ありませんが,そんなに難しくないので,時間のある人はついでに読んで見てください.
lemma
ベクトル空間 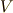 上の線形汎関数
上の線形汎関数 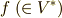 と任意の元
と任意の元  に対し,
に対し, 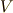 には
には 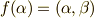 を満たす
を満たす 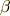 が必ず存在します.
が必ず存在します.
線形汎関数によって,ベクトルはスカラーに移されます.一方,内積という計算も線形汎関数だと見ることができました( 内積と双対空間 参照).この定理の主張が当たり前に思えた人は,かなり数学の考え方に馴れてきていると思って良いでしょう.
proof
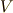 の正規直交基底を
の正規直交基底を 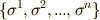 とし,
とし, 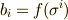 と置きます.
と置きます. 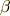 として,
として,  とおけば,
とおけば, 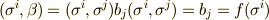 が成り立ちます.任意の
が成り立ちます.任意の 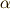 は
は 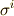 の一次結合で書けるため,定理が示されます.■
の一次結合で書けるため,定理が示されます.■
空間の符号定数について補足
先ほど,註でミンコフスキー空間について少し触れました.ミンコフスキー空間の正規直交基底を 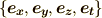 のように取れば(
のように取れば( 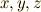 は空間軸,
は空間軸, 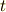 は時間軸の意味とします),最初の三つの基底については普通に
は時間軸の意味とします),最初の三つの基底については普通に 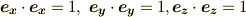 が成り立ちますが,時間軸の基底については
が成り立ちますが,時間軸の基底については 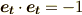 となるのでした.つまり,内積が正になる基底が
となるのでした.つまり,内積が正になる基底が 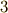 つ,負になる基底が
つ,負になる基底が 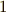 つです.この個数の配分は,基底をいかに直交変換しても変わりません.
つです.この個数の配分は,基底をいかに直交変換しても変わりません.
一般に, 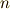 次元のベクトル空間の基底で,内積が正になるものが
次元のベクトル空間の基底で,内積が正になるものが  個,内積が負になるものが
個,内積が負になるものが  個あるとき(
個あるとき(  ),
), 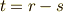 という数は空間に固有のもので,基底の取り方にはよらない定数となります.これを 符号定数 と呼びます.ミンコフスキー空間では,
という数は空間に固有のもので,基底の取り方にはよらない定数となります.これを 符号定数 と呼びます.ミンコフスキー空間では, 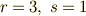 ですから,
ですから, 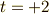 となります.
となります. 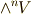 の正規直交基底を
の正規直交基底を  と置くとき,このn-ベクトルの内積は
と置くとき,このn-ベクトルの内積は 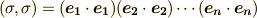 となりますので,
となりますので,  の偶奇によって
の偶奇によって 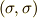 の符号も変わり,
の符号も変わり, 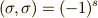 と表わせることが分かります.いま,この段階であまり細かく考える必要はありませんが,何となく,空間の基底について,こんな話があったことを覚えておいて下さい.
と表わせることが分かります.いま,この段階であまり細かく考える必要はありませんが,何となく,空間の基底について,こんな話があったことを覚えておいて下さい.
| [♥] | 符号定数については正負を逆にする流儀もあります.その流儀に従えば, 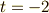 となります.ややこしい話ですが,世の表記が統一されていない以上しょうがないです.自分で本を読む場合には注意して下さい. となります.ややこしい話ですが,世の表記が統一されていない以上しょうがないです.自分で本を読む場合には注意して下さい. |
| [♦] | 符号定数 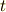 を用いれば, を用いれば, 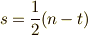 と表わすこともできます. と表わすこともできます. |