内積と双対空間
ベクトルの内積を,ベクトル空間や双対空間といった代数的な視点からもう一度考えてみます.ベクトル 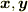 の内積は一般にスカラーになりますから,スカラー
の内積は一般にスカラーになりますから,スカラー 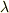 を使って次のように表わせるとします.
を使って次のように表わせるとします.

内積は二つのベクトルに関して対称ですが,ここで仮に内積という演算を 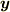 に作用する関数と見て次のように書いてみましょう.
に作用する関数と見て次のように書いてみましょう.

ちょっと見方を変えてみただけで,式 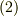 の意味は式
の意味は式 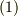 と全く同じです.しかし,こうやって違う記号で眺めてみると面白いことが見えてきます.関数
と全く同じです.しかし,こうやって違う記号で眺めてみると面白いことが見えてきます.関数 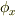 は内積の性質から言って,次式を満たします.
は内積の性質から言って,次式を満たします.
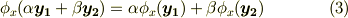
この形を見てピンと来て欲しいところですが, 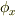 はベクトル空間
はベクトル空間 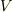 の元
の元 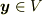 に対する線形関数になっています.(線形関数の定義は ベクトル空間と線形写像 を参照して下さい.)特に,
に対する線形関数になっています.(線形関数の定義は ベクトル空間と線形写像 を参照して下さい.)特に, 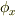 は
は 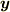 をスカラー
をスカラー 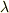 に対応させる写像ですから線形汎関数になっており,
に対応させる写像ですから線形汎関数になっており, 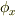 は
は 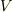 の双対空間
の双対空間 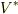 の元だと考えられます.(線形汎関数と双対空間については 双対空間 を参照.)
の元だと考えられます.(線形汎関数と双対空間については 双対空間 を参照.)
ベクトル 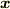 に対して
に対して 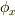 は一つに決まりますので,この対応を写像
は一つに決まりますので,この対応を写像 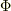 で表わすことにしておきます.
で表わすことにしておきます.

式 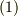 を
を 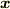 に対する関数
に対する関数 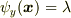 と見ても良いことを考えると,この写像
と見ても良いことを考えると,この写像 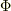 は,内積の線形性より
は,内積の線形性より 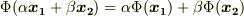 を満たすはずで,線形写像であることが分かります.ただの内積の話が,なんだかアヤシイ感じになってきましたね.内積を線形関数だなんて考えてみたことのなかった人は吃驚したかも知れません.
を満たすはずで,線形写像であることが分かります.ただの内積の話が,なんだかアヤシイ感じになってきましたね.内積を線形関数だなんて考えてみたことのなかった人は吃驚したかも知れません.
Important
内積は線形汎関数だと見ることもできる.
この写像, 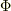 は一体どのような種類の写像なのかと言えば,
は一体どのような種類の写像なのかと言えば, 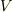 と
と 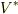 の 同型写像 です.
の 同型写像 です.
theorem
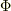 は同型写像
は同型写像 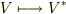 です.
です.
proof
いま示したいのは『 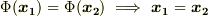 』です.
』です. 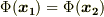 は
は 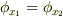 と同じ条件ですから,結局,『全ての
と同じ条件ですから,結局,『全ての 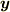 に対して
に対して 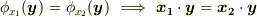 』を示せば良いことになります.
』を示せば良いことになります. 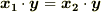 は
は 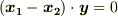 と変形できますが,いま
と変形できますが,いま 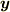 としては任意のベクトルを選んでいますので,全ての
としては任意のベクトルを選んでいますので,全ての 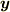 に対してこの条件が満たされることになります.ということは,
に対してこの条件が満たされることになります.ということは, 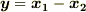 を選んでも良いはずですが,そうすると
を選んでも良いはずですが,そうすると 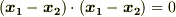 を得ます.このとき
を得ます.このとき 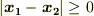 より,
より, 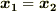 が要請され,『
が要請され,『 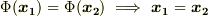 』が示されます.このとき
』が示されます.このとき 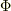 による写像
による写像 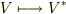 は一対一写像で,同型写像となります.■
は一対一写像で,同型写像となります.■
ここまでの議論を整理しておきましょう.最初は,ベクトル空間 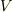 の元
の元 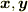 に内積を定義しただけですが,内積を線形汎関数と考えることで,
に内積を定義しただけですが,内積を線形汎関数と考えることで, 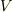 と双対空間
と双対空間 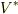 の間に同型写像
の間に同型写像 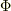 が与えられてしまいました.
が与えられてしまいました.
Important
内積は,ベクトル空間 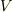 とその双対空間
とその双対空間 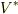 の間に同型写像を与えます.
の間に同型写像を与えます.
内積の意味は,今までにも色々な記事で議論してきました.図形的に絵を考えてみたり,『二つのベクトルの似ている度合いを測る指標だ』というような説明もありました.ベクトル空間に距離関数を導入するという役割もありました.いま,全く代数的な視点から『内積はベクトル空間と双対空間の間に同型写像を与える』という役割も見えてきたわけです.
実際に計算してみる
『内積が同型写像を与える』とはどういうことか,実際に計算して考えてみましょう.ベクトル空間 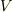 の基底を
の基底を 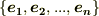 ,双対空間
,双対空間 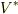 の基底を
の基底を 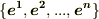 とします.
とします.
また,基底同士の内積は 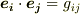 ,もしくは
,もしくは 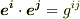 と置きます.( 計量テンソル 参照.)いま,ベクトル空間
と置きます.( 計量テンソル 参照.)いま,ベクトル空間  の元
の元  は基底
は基底  を使って次のように表現できるでしょう.
を使って次のように表現できるでしょう.
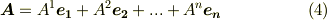
このとき,双対基底の性質 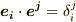 により,次式がなりたちます.
により,次式がなりたちます.

一方,  と
と 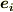 の内積を考えると,計量テンソルを使って次式のように表現できます.
の内積を考えると,計量テンソルを使って次式のように表現できます.
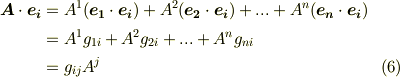
式 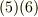 より次式を得ます.
より次式を得ます.
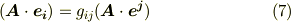
なんだか面白い形に帰着しました.  は任意の関数でしたから,両辺の内積を『
は任意の関数でしたから,両辺の内積を『  の関数』と考えれば,形式的に次のように書けます.括弧の右側が開いているのは,右から何かベクトルが作用するのを待っている状態だということを少し大袈裟に表現してみただけです.
の関数』と考えれば,形式的に次のように書けます.括弧の右側が開いているのは,右から何かベクトルが作用するのを待っている状態だということを少し大袈裟に表現してみただけです.

前セクションで,ベクトル 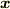 を
を 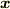 との内積
との内積 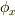 に対応させる同型写像
に対応させる同型写像 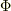 を考えましたが,
を考えましたが, 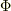 を使えば,式
を使えば,式 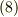 は双対基底と
は双対基底と 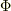 の間に次の写像関係があることを主張している式だと見ることができるでしょう.
の間に次の写像関係があることを主張している式だと見ることができるでしょう. 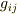 が
が 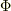 に当たります.
に当たります.

ベクトル空間 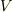 から双対空間
から双対空間 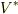 への写像という文脈で,計量テンソル
への写像という文脈で,計量テンソル 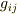 が果たしている役割がよく分かると思います.
が果たしている役割がよく分かると思います. 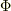 は同型写像ですから逆写像がありますし,
は同型写像ですから逆写像がありますし, 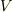 と
と 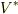 は双対ですから,当然次式もなりたちます.
は双対ですから,当然次式もなりたちます.
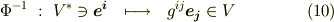
実は,式 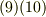 は『添字の上げ下げ』として知られる操作で, 計量テンソルとヤコビアン で勉強します.単に『添字の上下を入れ換える』という機械的操作として
は『添字の上げ下げ』として知られる操作で, 計量テンソルとヤコビアン で勉強します.単に『添字の上下を入れ換える』という機械的操作として 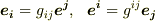 を暗記している人もいると思いますが,内積が線形関数だと考えられること,内積によってベクトル空間と双対空間の間に同型写像を入れられること,この一対一対応によってベクトル空間の基底
を暗記している人もいると思いますが,内積が線形関数だと考えられること,内積によってベクトル空間と双対空間の間に同型写像を入れられること,この一対一対応によってベクトル空間の基底 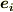 と双対空間の基底を関係付けられること等を,きちんと数学的に頭の中で整理しておくと添字に対する洞察が深まると思います.
と双対空間の基底を関係付けられること等を,きちんと数学的に頭の中で整理しておくと添字に対する洞察が深まると思います.
Important
計量テンソルで添字を上げたり下げたりするのは, 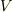 と
と 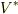 を行ったり来たりする写像です.
を行ったり来たりする写像です.
上下に分かれた添字のシステムがよく出来ていることをだんだんと実感して来て頂けると良いです.