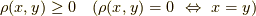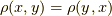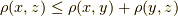内積空間
この記事の内容は,ここまで考えてきた双対基底や,共変ベクトル,反変ベクトルといった話題とは直接関係ありません.しかし,せっかくベクトル空間や双対空間など,抽象的な概念を紹介しましたので,ついでにもう一つ,内積空間について勉強してしまおうと思います.
今すぐに大事なのは『ベクトル  の長さは
の長さは 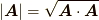 と定義する』という式だけです.その他の部分は,内積,角度,図形の長さといった概念に関する数学的背景ですので,興味の無い人は読まないで先へ進んでも大丈夫です.
と定義する』という式だけです.その他の部分は,内積,角度,図形の長さといった概念に関する数学的背景ですので,興味の無い人は読まないで先へ進んでも大丈夫です.
長さとは?
復習になりますが,ベクトル空間とは,ベクトルの満たす加法とスカラー積の演算法則を抽象化し,一般化した概念でした.
しかし,まだこれだけでは幾何学を始めるのに十分ではありません.(普通の)幾何学をするには,さらに『長さの概念』を導入しなければなりません.元の間に長さが定義されている集合を 距離空間 と呼びます.
| [*] | 私たちの日常の感覚から言うと,何か物が二つあれば「距離」があるのは当たり前な気がしますが,数学では決して当たり前のことではないのです.まず,議論の対象とする物の集合を考えるわけですが,ただ寄せ集めただけでは,それは単なる集合であって,その元の間には距離も演算もまだ何にも定義されていません.現代の数学の議論の出発点はまさに「何にもない」ところであって,普段当たり前だと思っていることさえ自分で決めていかなければならないのです.慣れていない人にとっては,普段当たり前だと思っている概念に関する議論の方が,あまりに本質的なだけにかえって難しく感じるものです.ちょうど,必要なソフトが全て最初からインストールしてあるパソコンしか使ったことの無かった人が,いきなり自分でパソコンを組み立てろと言われたような感覚でしょう.当たり前だと思っていたことほど,どういう仕組みになっているのか知らなかったりするものです.私達は数学者ではありませんから,あまり哲学的な問題に深入りする必要はありません.しかし,こういった数学的議論を省略せずに追っていくと,日頃当たり前に思えていたことに対してパッと深い理解が得られたりします.こんな経験をしてしまうと,数学は楽しくてやめられません. |
少し脇道に逸れますが, 位相 という概念を紹介しておきましょう.位相は,幾何学性質として距離よりももっと弱い概念です.(数学者と物理学者で位相を違う意味に使う場合があるので注意して下さい. 位相空間 を参照してください.)距離の概念が入っていないと,『大きい・小さい』『遠い・近い』『長い・短い』などの概念が一切存在しない世界になります.そんなんで幾何学ができるの?と思いますが,そこに位相という概念さえあれば, 連続や極限といった概念 を入れることはできますので,例えば図形が『つながっているか・切れているか』というような区別は出来ることになります.そこで『穴の開いている図形と穴の開いていない図形』『引っ張ったら輪の形にほどける結び目と輪の形には絶対ならない結び目』などが区別される世界になります.

この結び目,どんなに引っ張っても輪っかにはならない.
位相だけ入った世界で考える幾何学の分野を「位相幾何学」と呼びますが,位相幾何学の世界では,曲げたり伸ばしたり,ねじったり引っ張ったりしても,どうにも同じにならない図形だけを違うものと区別します.これは相当に豊潤な内容を含んだ興味深い分野で,現代数学の中でも最も重要な分野の一つでもあります.
| [†] | 直観的イメージとしては,位相幾何は伸縮自在な物質でできた世界の幾何学という感じです.それに比べると,距離の入った幾何学はガッチリと硬い物質の幾何学です. |
数学者にとっては,空間に位相が入っていないとなかなか幾何学が出来ませんが,位相さえ入っていれば,距離が入っていなくてもかなり面白い世界があるということを伝えたくて,敢えて脇道に逸れました.また,順序としては,距離を入れる前に,まず位相を入れるということも重要です.位相の話は簡単に済むようなものではないので,この記事では特に触れずにこのまま先に進みます.距離が定義されている世界というのは,数学的にはかなりきっちりした,強い条件を備えた世界なんですね.『距離なんて,あって当たり前やん!』と思っていた人が,少しでも見方を変えていただければ幸甚です.

新品のパソコンに,必要なソフトを順番にインストールしていくようなものだ.
さて,私達は幾何ベクトルを使って(普通の)幾何学をすることが念頭にありますから,距離を定義しましょう.一足飛び距離を定義してしまえば,位相も自動的に入りますので,私達はとりあえず位相のことは忘れても大丈夫です.
| [‡] | 普通の人の感覚では,紙の上に線を引けば誰がどう見ても距離がありますし,円を書けばどうみても面積がありますから,距離が無いという意味がよく分からないと思います.これはもっともな感覚で,十九世紀までの数学者の多くもこんなことをうるさくは言いませんでした.二十世紀に入り,数学を公理論的に再構成しようという動きが活発になりました.その中心となったのは ブルバキ ですが,まったく何も決まっていない集合から始めて公理的に代数構造や概念を付与していき,無矛盾に数学の体系を作ろうという試みです.結局,途中で新しい数学分野が発達してきたことや,集合論的アプローチがそれほど珍しいものではなくなったこともあり,ブルバキの活動は尻すぼみに終わりましたが(いまも細々続いているようです),現代的な数学の出発点となった功績は偉大です.きっちりゼロから数学の体系を作ろうとすると,論理の順番として必ずしも私達に馴染みのある概念が先に出てくるわけではないようです.距離の概念を入れる,と聞いて『何を当たり前なことを!』と思うかも知れませんが,より抽象性の高い話へ進むには,当たり前のことをきっちり踏まえて置かねばなりません.少しずつ現代的な数学の方法にも慣れていきましょう.使えるようになれば,非常に強力な武器になるはずです. |
距離
集合の元を二つとってきて,その元 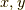 に対して次の性質を満たす関数
に対して次の性質を満たす関数  を決めることができるとき,抽象的な立場ではこれを 距離 と呼ぶことにします.
を決めることができるとき,抽象的な立場ではこれを 距離 と呼ぶことにします.
繰り返しになりますが,集合の元は何だか分かりませんから,この関数は,私達が日常的にイメージする「距離」とは全くイメージの懸け離れたものである場合もあります.とにかく,上記  〜
〜 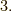 を満たす関数をキョリと呼んでしまおうということです.また,一つの集合に複数の距離関数を定義できる場合もあります.
を満たす関数をキョリと呼んでしまおうということです.また,一つの集合に複数の距離関数を定義できる場合もあります.
内積
まず,私達が普通に知っている内積によって, ベクトル空間に距離(の概念)を導入できる ことを見ましょう.ベクトルの大きさを,内積を使って次のように定義します.

すると,式 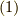 の定義を使い,ベクトル空間の二つの元
の定義を使い,ベクトル空間の二つの元 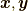 の距離
の距離 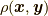 を次のように定義できます.
を次のように定義できます.

距離関数 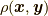 が,距離関数の定義
が,距離関数の定義 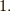 〜
〜 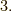 を満たすことを確認してください.このように,内積を定義したことでベクトル空間には距離が入り,はじめて長さを使った普通の幾何学ができるようになったのです.
を満たすことを確認してください.このように,内積を定義したことでベクトル空間には距離が入り,はじめて長さを使った普通の幾何学ができるようになったのです.
高校数学のベクトル分野では,『ベクトルに長さがあること』もしくは『ベクトルの計算をする紙の上に距離があること』は暗黙の前提になっていました.ですから,式  は,(なんだか意味のよく分からない)内積という演算を習った際,『自分自身との内積』という特別な場合として少し出てくる程度の扱いだったと思います.
は,(なんだか意味のよく分からない)内積という演算を習った際,『自分自身との内積』という特別な場合として少し出てくる程度の扱いだったと思います.
今までの議論について来た人は,高校数学と現代数学が,全く逆の立場であることに気がつくことでしょう.ベクトル空間には,私達が内積を定義するまでは距離が無い(距離という概念さえ無い)のです.式 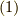 によって初めて『長さの概念が導入された』のであって,幾何学をする準備が整ったと言えるわけです.内積とは,そのように重要な演算規則なのでありました.
によって初めて『長さの概念が導入された』のであって,幾何学をする準備が整ったと言えるわけです.内積とは,そのように重要な演算規則なのでありました.
内積の概念を拡張
私達の考えていたベクトル空間は抽象的な集合で,幾何ベクトルと同じ加法とスカラー積演算を満たすものならば,元は何でも良いということでした.幾何ベクトルの集合に距離の概念を導入するため,内積 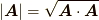 という演算を定義しましたが,幾何ベクトル以外の色々な集合にも内積を定義することで,同様にして距離に似た概念を導入することが出来ます.
という演算を定義しましたが,幾何ベクトル以外の色々な集合にも内積を定義することで,同様にして距離に似た概念を導入することが出来ます.
ただし,ベクトル空間の元には関数,演算子,行列など,色々なものが可能ですから,ここで導入される概念は,普段私達が言うところの「距離」とは少し違うものになるはずです.そこで,距離とは言わず, ノルム と呼ぶことにします.
| [§] | このように,内積という演算を通じて距離の概念を一般化したものはノルムになりますが,内積を使わなくても,距離空間の定義を満たすために定義した抽象的距離をノルムと呼べます.ノルムは,内積を使って定義した距離よりも一般に弱く,かつ広い概念です.内積からは距離の他に後述するように角度の概念も出てきますが,ノルムを決めるのに必ずしも角度の概念は必要ありません. |
問題は内積の方です.一般的に,ベクトル空間の二つの元  の間に,次の条件を満たす演算が定義できれば,この演算を 内積 と呼んでしまうことにします.私達の知っている幾何ベクトルの内積を一般化したものです.
の間に,次の条件を満たす演算が定義できれば,この演算を 内積 と呼んでしまうことにします.私達の知っている幾何ベクトルの内積を一般化したものです.
【一般化された内積】
- 線形性がある.

- 対称性がある.
- 正定値性がある.
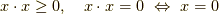
内積の定義されているベクトル空間を 内積空間 と呼びます.
| [¶] | 一番目の性質について内積を二変数の関数 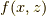 と見ると,内積とは と見ると,内積とは 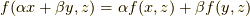 を満たす関数なのだと考えられます.このような性質を満たす関数を双線形関数と呼びます.二つの変数に対して,それぞれ線形性が成り立っているからです.内積とは,ベクトル空間 を満たす関数なのだと考えられます.このような性質を満たす関数を双線形関数と呼びます.二つの変数に対して,それぞれ線形性が成り立っているからです.内積とは,ベクトル空間 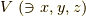 上の 双線形関数 である,と見ることもできます. 上の 双線形関数 である,と見ることもできます. |
角度
三番目の定義より, 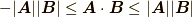 ( シュヴァルツの不等式 )を導けます.ここでは証明は省略します.シュヴァルツの不等式に
( シュヴァルツの不等式 )を導けます.ここでは証明は省略します.シュヴァルツの不等式に 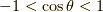 を利用すると,一般に二つのベクトルの内積を次のように表現しても良いことが分かります.
を利用すると,一般に二つのベクトルの内積を次のように表現しても良いことが分かります.
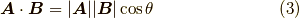
このようにして,内積の定義とシュヴァルツの不等式を通じて 角度の概念 も導入することができました.
例1
ベクトル空間の元が関数の場合,次の演算 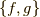 は内積の定義
は内積の定義 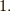 〜
〜 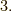 を満たしますので,広い意味での内積になっています.(確認してみて下さい.)
を満たしますので,広い意味での内積になっています.(確認してみて下さい.)

また,ノルムを ![\displaystyle \big\Arrowvert f\big\Arrowvert =\Bigg(\int _{b}^{a}[f(x)]^{2}dx\Bigg)^{1\over 2}](./62752b2f90345028d8f58f005677b010.png) で定義し,距離関数を
で定義し,距離関数を  と定義すれば,この
と定義すれば,この 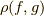 は距離関数の定義を満たしますので,関数を元とするこのベクトル空間も距離空間になります.(距離関数の定義を満たすことも確認してみて下さい.)なんだか変な奴らが出てきましたね.数学的に,距離の概念をこんな関数の集合にまで広げられるということです.
は距離関数の定義を満たしますので,関数を元とするこのベクトル空間も距離空間になります.(距離関数の定義を満たすことも確認してみて下さい.)なんだか変な奴らが出てきましたね.数学的に,距離の概念をこんな関数の集合にまで広げられるということです.
一般的に,関数の間の角度と言われても意味がよく分かりませんので, 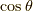 は決めませんが,幾何ベクトルの直交関係
は決めませんが,幾何ベクトルの直交関係 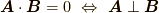 から言葉を借りてきて,特に内積が零となる場合を 関数が直交する と呼ぶことにします.
から言葉を借りてきて,特に内積が零となる場合を 関数が直交する と呼ぶことにします.
単なる言葉の借用ですから,直交と言っても何かが直角になっているという訳ではありません.日常的な意味での,距離という言葉から連想するイメージからは離れた方が良いでしょう.
| [#] | このように,内積を導入すると距離と角度という概念を空間に導入できます.距離というのは,先述したように位相よりも強い概念ですから,距離空間は自動的に位相空間にもなっています.また,距離空間になるためには,定義上かならずしも角度の概念までは必要なく,そのようなノルムによって決めた距離空間をノルム空間,もしくはノルム線形空間などと呼んで区別することもあります.これも内積空間よりは弱い概念です.今は,あまり細かい用語や区別を覚えようとしなくても大丈夫です.もう少し詳しくこの辺りの話を知りたい人は,集合と位相,関数解析といった題名の教科書を読んでみて下さい. |
内積の直観的理解
よく使うので関数の内積を例に出しましたが,他にも色々なベクトル空間に対して,色々な種類の内積が考えられることでしょう.抽象化してしまうと図形的意味はよく分からなくなりますが,「内積の役割」とも言うべき,一番重要な性質がかえってクローズアップされてくると思います.
内積を関数と考えることも出来ます.二つのベクトルを放り込むと,一つのスカラーが返って来るという関数です.幾何ベクトルのイメージに戻って,少し意味を考えてみましょう. 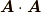 のように同じベクトルの内積は,そのベクトルの長さの二乗になります.一方,長さが同じでも向きが
のように同じベクトルの内積は,そのベクトルの長さの二乗になります.一方,長さが同じでも向きが 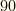 度ずれていれば内積は零になってしまいます.二つのベクトルの内積も,『向きが同じなら最大値』『真横を向いていれば零』になってしまいます.どうやら, 内積とは,二つのベクトルがどれくらい同じ方向を向いているかを示す比 だと言えそうです.
度ずれていれば内積は零になってしまいます.二つのベクトルの内積も,『向きが同じなら最大値』『真横を向いていれば零』になってしまいます.どうやら, 内積とは,二つのベクトルがどれくらい同じ方向を向いているかを示す比 だと言えそうです.
| [♠] | 最初原稿を書いたとき,『真横を向いていれば零』の部分を『そっぽを向いていれば零』としました.少し擬人化した表現のほうが直観的に訴えると思ったからですが,そっぽというのはどうも古臭い表現ですし, 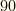 度横がそっぽだと思う人もいれば 度横がそっぽだと思う人もいれば 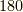 度がそっぽだと思う人もいるかも知れないのでやめました.『一番関係ない向き』と書けば良かったでしょうか.ベクトルにとって互いに一番関係ない向きは 度がそっぽだと思う人もいるかも知れないのでやめました.『一番関係ない向き』と書けば良かったでしょうか.ベクトルにとって互いに一番関係ない向きは 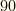 度っていうのは,直観的に自明なのかな.日本語は難しいですね. 度っていうのは,直観的に自明なのかな.日本語は難しいですね. |
内積をさらに一般のベクトル空間にも拡張するとき,例えば関数や演算子に対して『向き』という意味はよく分かりませんから,『似ている・似ていない』と言い換えればよいでしょう.この意味でシュヴァルツの不等式 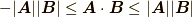 は意味深です.シュヴァルツの不等式は,二つの(抽象的な意味での)ベクトルに対し,"似ている度"の範囲を表わす不等式なのですね.
は意味深です.シュヴァルツの不等式は,二つの(抽象的な意味での)ベクトルに対し,"似ている度"の範囲を表わす不等式なのですね.
Important
内積は,二つのベクトルがどれくらい似ているかを示す.
.
| [♥] | フーリエ展開を勉強すると,関数の集合をベクトルのように扱うため,内積,関数の直交,基底,などベクトルで使っていた用語がたくさん流用されます.また,内積の定義された無限次元の複素ベクトル空間をヒルベルト空間と呼んだりします.(ヒルベルト空間では,もう一つ完備性という性質も重要ですが,この記事の範囲を逸脱するためここでは説明しません.)量子力学を勉強するとヒルベルト空間が出てくるため,嬉しくて必要以上にこの立派な名前を人前で使いたがる人がおり,初めて聞く人はビックリしてしまったりします.ここまでこの記事を読んだ人にとって,ヒルベルト空間なんて別に難しい概念ではありません. |
いまのうちに,内積,距離,距離空間などの知識を整理しておくと,意外に先々見通しが良くなると思います.

いま内積占いが大流行だ.
まとめ(おさらい)
ベクトル空間は,ベクトルの加法とスカラー積の性質を抽象化・一般化した集合でした.そこには距離(長さ)の概念は入っていません.そこで,私達は内積という演算 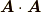 を定義し,ベクトルの大きさを
を定義し,ベクトルの大きさを 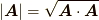 と定義しました.これによって距離
と定義しました.これによって距離 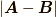 を決めることができ,ベクトル空間は距離空間になりました.
を決めることができ,ベクトル空間は距離空間になりました.
ただし,距離空間の定義は一般にもっと抽象的で,私達が言葉から想像する距離とはちょっと違ったものを距離と定めても,数学的には距離空間と言えるのでした.そのような距離の概念を拡張したものをノルムと呼ぶのでした.ノルムを距離と呼んでしまっては語弊があります.元(げん)同士の「近さ」を表わす一種の尺度だと考えておきましょう.ノルムを距離関数と考えることで,一般のベクトル空間も距離空間になれます.距離の概念が導入されたベクトル空間を, 計量をもつベクトル空間 もしくは単に 計量ベクトル空間 と呼んだりします.
抽象的な数学の立場では,集合に距離があるかどうかは自明ではありませんので,ちゃんと自分で定義してやらねばなりません.また,距離を入れる前に,順番として位相という概念を入れる必要があります.位相を入れると集合の元に連続や極限といった概念を導入できます.図形がつながっているか,切れているかといった関係は位相だけで分かります.そのうち位相もきちんと勉強しましょう.いまは,距離を入れれば自動的に位相も入ってしまうので,位相にこだわらなくても大丈夫です.
一般のベクトル空間にも,内積を定義できました.内積が決まれば,幾何ベクトルと同様,自分自身との内積の平方根を取ることで距離の概念を導入することができました.つまり,内積という演算は距離を与えます.しかも,内積からは角度の概念も出てきますので,かなり幾何学をする準備が整います.ノルムの一般的な定義に角度の定義は不必要ですので,内積によって定められる距離やノルムは,かなり強い条件を持った概念だと言えます.
一般に,距離や角度を使って普通の幾何学をやりたければ,集合に内積を決めないといけません.あえて乱暴な言い方をしますが,物理にちょくちょく出てくるヒルベルト空間とは内積を定義したベクトル空間であって,その理由は,普通の幾何学をしたいからです.特に断らない限り,このあと私達が考えるベクトル空間には内積が定義されており,距離や角度も考えられるとします.
| [♦] | 内積の重要性はベクトル空間に距離を入れることにありました.では,外積はどうなんでしょう?外積には,図形的にそのような決定的な役割はありません.名前からの連想か,内積と外積を兄弟のように思っている人がいますが,確かに一定の関係はあるものの,そんなに似た演算ではありません.外積の演算規則を一般化した世界は,外積代数という分野で,これは非常に面白い代数です.いずれ物理のかぎしっぽでも,外積代数を取り上げる予定です.さらに微分形式の理論,クリフォード代数などへ発展するともっと面白い世界が広がっています.わくわくします. |