イデアルで外積代数を入れる3
この記事は, イデアルで外積代数を入れる2 の続きです.代数学に関係する部分をかなりゆっくり説明して来ましたが,いよいよ最後です.私達は,テンソル空間 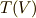 に対し,
に対し, 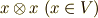 を含む最小のイデアル
を含む最小のイデアル 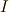 を考え,その商代数
を考え,その商代数 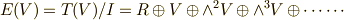 を求めました.この記事では,テンソル代数の乗法ともいうべきテンソル積
を求めました.この記事では,テンソル代数の乗法ともいうべきテンソル積 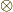 を,
を, 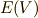 に移した乗法
に移した乗法 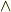 を考え,この乗法が 外積代数 で定義したウェッジ積の乗法であることを確認します.そして,いよいよ
を考え,この乗法が 外積代数 で定義したウェッジ積の乗法であることを確認します.そして,いよいよ 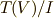 が外積代数であることを最終確認するという流れです.
が外積代数であることを最終確認するという流れです.
商代数の乗法
まず,商代数 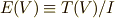 を次のように置きます.ギリシャ文字
を次のように置きます.ギリシャ文字 ![[\alpha ]](./33fa5586bb2a2453ab5576575bfd5cd5.png) などはスカラー
などはスカラー 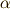 を代表元とする類,小文字の
を代表元とする類,小文字の ![[x]](./788781478040b502fd4550005057a125.png) などはベクトル
などはベクトル  を代表元とする類とします. イデアルで外積代数を入れる2 までの議論により,
を代表元とする類とします. イデアルで外積代数を入れる2 までの議論により, 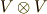 以上の階数のテンソルは,全てこれらの類に類別されています.
以上の階数のテンソルは,全てこれらの類に類別されています.
まず,次の関係が言えます.
theorem
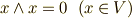
proof
イデアルの定義より 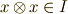 で,イデアルは常に
で,イデアルは常に 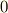 を含むので
を含むので 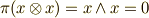 となります.■
となります.■
さらに,次の関係も言えます.
theorem
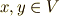 に対し
に対し 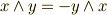 となります.
となります.
proof
前定理より, 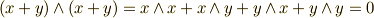 がなりたちます.
がなりたちます. 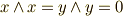 を代入して,定理が示されます.■
を代入して,定理が示されます.■
どうやら,私達が得た 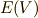 は,この
は,この 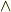 による乗法を考えることで,外積代数になっているようです.( 外積代数 で考えたウェッジ積の乗法を思い出してください.)
による乗法を考えることで,外積代数になっているようです.( 外積代数 で考えたウェッジ積の乗法を思い出してください.)
| [*] | 外積代数 の記事では,いきなり天下り的に外積代数の算法を定義しました.外積代数の威力が発揮されるのは,外積代数そのものと言うよりも,微分形式の理論においてですから,早く先に行きたい人が,外積代数の構造を公理的に受け容れ,そこから出発しても構いません.ただ,こんな代数をどう思いついたのか?という疑問を持つ人や,いきなり天下り的に出て来た物を受け容れるのに抵抗があった人が,こうやってテンソル代数とイデアルから外積代数が出てきたのを見て,すっきり安眠できれば良いと思っています.また,ここまで読んできた人は,ベクトル空間→テンソル空間→外積代数→微分形式という流れが連続して見えてきたのではないでしょうか. |
外積代数の構造(つづき)
テンソル代数 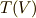 から外積代数
から外積代数 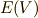 への写像
への写像  を考え,
を考え, 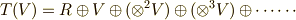 を写像したものを次のように書きました.ここまでは イデアルで外積代数を入れる2 の復習です.
を写像したものを次のように書きました.ここまでは イデアルで外積代数を入れる2 の復習です.
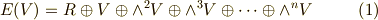
前セクションの二つの定理により, 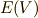 が外積代数であることが分かりましたので, 外積代数 の議論に従い,
が外積代数であることが分かりましたので, 外積代数 の議論に従い,  を
を  次元のベクトル空間とすれば,
次元のベクトル空間とすれば, 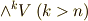 は全て
は全て  になることが分かります.そこで,式
になることが分かります.そこで,式 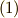 の右辺は無限に続くのではなく,
の右辺は無限に続くのではなく, 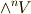 までで打ち止めになります.
までで打ち止めになります.
| [†] | 式 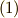 の右辺が,和 の右辺が,和 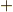 ではなく,直和 ではなく,直和 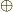 で書ける理由は,各外積空間 で書ける理由は,各外積空間 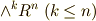 が独立だからです.本当は,次元の異なる外積空間が独立であることも,きちんと証明すべきです. が独立だからです.本当は,次元の異なる外積空間が独立であることも,きちんと証明すべきです. |
蛇足ですが,各  に対しては次式が成り立ちました.(
に対しては次式が成り立ちました.(  個から
個から 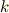 個選ぶ組み合わせは
個選ぶ組み合わせは 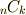 通りです.これが,そのまま外積空間
通りです.これが,そのまま外積空間 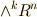 の次元になるのでした.)
の次元になるのでした.)
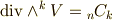
従って, 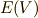 の次元に関しては次式が成り立ちます.
の次元に関しては次式が成り立ちます.
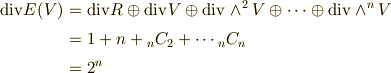
これは,二項係数の定理として,高校で習う公式です.外積代数 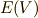 を,テンソル空間
を,テンソル空間 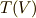 から作る話は以上で終わりです.お疲れ様でした.外積代数は,外積代数そのものというより,微分形式という表現を使うことで威力を発揮します.今まで勉強してきたのは,いわば微分形式の準備編です.ここまでの記事が全部よく理解できたという人は,既にかなり力があると自信を持って良いと思います.
から作る話は以上で終わりです.お疲れ様でした.外積代数は,外積代数そのものというより,微分形式という表現を使うことで威力を発揮します.今まで勉強してきたのは,いわば微分形式の準備編です.ここまでの記事が全部よく理解できたという人は,既にかなり力があると自信を持って良いと思います.
外積代数の誕生
外積空間を最初に考案したのは,ドイツの数学者,グラスマン( 
 )です.グラスマンの生い立ちは,既に 三重積 で紹介しましたが,グラスマンは若い頃は数学に興味がなく,大学では哲学,神学,ラテン語やギリシャ語などを勉強しました.大学卒業後,ようやく数学に興味が向き始め,独学を続けながらギムナジウム(ドイツの進学用中学・高校に相当)の教師になりましたが,教員試験の成績も芳しくなく,レベルの低いクラス専門の教師として働き始めました.より上級の教員試験に挑戦しつつ数学の研究も続けたグラスマンは,
)です.グラスマンの生い立ちは,既に 三重積 で紹介しましたが,グラスマンは若い頃は数学に興味がなく,大学では哲学,神学,ラテン語やギリシャ語などを勉強しました.大学卒業後,ようやく数学に興味が向き始め,独学を続けながらギムナジウム(ドイツの進学用中学・高校に相当)の教師になりましたが,教員試験の成績も芳しくなく,レベルの低いクラス専門の教師として働き始めました.より上級の教員試験に挑戦しつつ数学の研究も続けたグラスマンは, 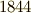 年,
年, 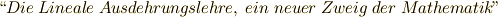 (線形拡大論,数学の新しい分野)という,ベクトルの理論と外積代数に関する画期的な著作を発表しました.これは,非常に抽象的で難解であり,当初は研究の重要性があまり理解されなかったようです.その後も本や論文の発表を続け,徐々に他の数学者達に認められるようになりますが,グラスマンに特徴的なのは,最初からかなり抽象的なベクトル空間論を用いている点です.当時一流の数学者にとっても,新しい概念を具体例なしで理解するのは簡単なことではありませんでした.グラスマンは,現在,ベクトル解析や線形代数と呼ばれる分野をほぼ独力で開拓し,外積代数も全くオリジナルなアイデアでした.微分幾何や多様体論といった分野にも深く関係し,真に時代に先駆けたものでしたが,人々に理解されるまでに多少の時間を要しました.
(線形拡大論,数学の新しい分野)という,ベクトルの理論と外積代数に関する画期的な著作を発表しました.これは,非常に抽象的で難解であり,当初は研究の重要性があまり理解されなかったようです.その後も本や論文の発表を続け,徐々に他の数学者達に認められるようになりますが,グラスマンに特徴的なのは,最初からかなり抽象的なベクトル空間論を用いている点です.当時一流の数学者にとっても,新しい概念を具体例なしで理解するのは簡単なことではありませんでした.グラスマンは,現在,ベクトル解析や線形代数と呼ばれる分野をほぼ独力で開拓し,外積代数も全くオリジナルなアイデアでした.微分幾何や多様体論といった分野にも深く関係し,真に時代に先駆けたものでしたが,人々に理解されるまでに多少の時間を要しました.

新しい分野を次々に作ったグラスマン.並大抵のことではない.
ベクトル解析分野は,グラスマンやメビウス( 
 )といったドイツ系の数学者達とは独立に,ハミルトン(
)といったドイツ系の数学者達とは独立に,ハミルトン(  ),テイト(
),テイト(  ),マックスウェル(
),マックスウェル(  ),ギブス(
),ギブス(  ),ヘヴィサイド(
),ヘヴィサイド(  )といった,英米系の数学者・物理学者達によって,主に電磁気学への興味から発展させられて来ました.どちらの流派が優れていたかは分かりませんが,現在採用されている記法や用語は英米系の学者によるもので,グラスマンの考案によるものは,グラスマン記号とウェッジ積くらいしか残っていません.線形代数は,今でこそ大学の教養課程での必須科目となっていますが,このように重要視され始めたのは二十世紀に入ってからで,グラスマンの時代にはそこまで重要な分野だとは認識されていませんでした.また,外積代数が本当に威力を発揮するのは,エリー・カルタン
)といった,英米系の数学者・物理学者達によって,主に電磁気学への興味から発展させられて来ました.どちらの流派が優れていたかは分かりませんが,現在採用されている記法や用語は英米系の学者によるもので,グラスマンの考案によるものは,グラスマン記号とウェッジ積くらいしか残っていません.線形代数は,今でこそ大学の教養課程での必須科目となっていますが,このように重要視され始めたのは二十世紀に入ってからで,グラスマンの時代にはそこまで重要な分野だとは認識されていませんでした.また,外積代数が本当に威力を発揮するのは,エリー・カルタン  による微分形式の理論の発展を待たなくてはなりませんが,これもグラスマンの死後のことです.グラスマンの業績は,どうも生前には十分な評価を得ていなかったようで,少し気の毒です.
による微分形式の理論の発展を待たなくてはなりませんが,これもグラスマンの死後のことです.グラスマンの業績は,どうも生前には十分な評価を得ていなかったようで,少し気の毒です.