イデアルで外積代数を入れる2
テンソル代数 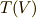 に対し,
に対し, 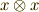 という元を含む最小のイデアル
という元を含む最小のイデアル 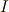 (
( 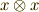 から生成したイデアルと呼びます)を考え,
から生成したイデアルと呼びます)を考え, 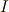 による
による 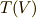 の商代数を考えました.
の商代数を考えました.
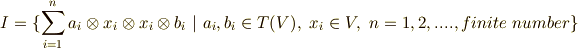
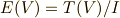
この 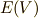 を外積代数と呼ぶ,ということでしたが,この記事では,この
を外積代数と呼ぶ,ということでしたが,この記事では,この 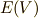 が,私達が最初に 外積代数 の記事で考えた構造を確かに持っていることを確認していきます.
が,私達が最初に 外積代数 の記事で考えた構造を確かに持っていることを確認していきます.
外積代数の元
イデアルが 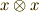 で生成される,という感じは掴めたでしょうか.イデアルの持つ吸収律(イデアルの元に何か掛けたらその積もイデアルになってしまうという性質)や,イデアル自身が一種の部分環で,イデアルの元のスカラー積や和について閉じているという性質により,かなり謙虚に『少なくとも一つ,
で生成される,という感じは掴めたでしょうか.イデアルの持つ吸収律(イデアルの元に何か掛けたらその積もイデアルになってしまうという性質)や,イデアル自身が一種の部分環で,イデアルの元のスカラー積や和について閉じているという性質により,かなり謙虚に『少なくとも一つ, 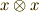 がイデアル
がイデアル 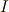 に含まれる』とイデアルを定義してみても,
に含まれる』とイデアルを定義してみても, 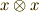 に関する積や和が,芋づる式に全てイデアルに含まれてしまうわけです.このため,
に関する積や和が,芋づる式に全てイデアルに含まれてしまうわけです.このため, 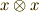 を含む最小のイデアルとは『
を含む最小のイデアルとは『 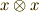 一個のみ』よりも,はるかに大きな集合にならざるを得ません.考えてみれば当然なんですが,なかなか最初はこの感覚に馴染まないかも知れません.
一個のみ』よりも,はるかに大きな集合にならざるを得ません.考えてみれば当然なんですが,なかなか最初はこの感覚に馴染まないかも知れません.
さて, 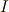 は
は 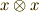 から生成されていますので,
から生成されていますので, 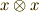 と何かの積(そしてそれらの和)というような形の元は,全て
と何かの積(そしてそれらの和)というような形の元は,全て 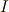 に含まれてしまっています.もう一度テンソル代数の定義を見てみましょう.
に含まれてしまっています.もう一度テンソル代数の定義を見てみましょう. 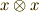 は単独では
は単独では 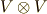 の元です.
の元です.
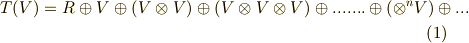
そして, 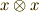 と,任意のテンソル
と,任意のテンソル 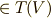 とのテンソル積は,最低でも
とのテンソル積は,最低でも 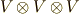 の元になるはずです.そして,それらの積や和が全てイデアルに含まれるということは,イデアル
の元になるはずです.そして,それらの積や和が全てイデアルに含まれるということは,イデアル 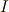 には
には 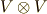 の元も
の元も 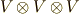 の元も,もっと高次のテンソル空間の元も全て含まれることになります.
の元も,もっと高次のテンソル空間の元も全て含まれることになります.
式 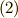 を,もう一度,式
を,もう一度,式 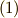 と比べてみましょう.
と比べてみましょう. 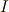 が含まないのは,
が含まないのは, 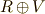 だけだという事が分かります.(生成元が
だけだという事が分かります.(生成元が 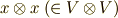 なので,最低でもイデアルの元は
なので,最低でもイデアルの元は 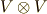 ってことですね.)これは重要な点で,これより,『
ってことですね.)これは重要な点で,これより,『 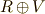 の元は全て異なる同値類に属する』ことが言えます.
の元は全て異なる同値類に属する』ことが言えます.
| [*] | ただし, 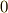 はイデアルの方に入っています. はイデアルの方に入っています. 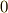 はいつだってイデアルです.いま議論している はいつだってイデアルです.いま議論している 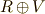 から から 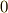 は除きます. は除きます. |

イデアルは何でも飲み込んでしまう.(適当に□と△と楕円で描いたら,かなり上図に描けてしまった・・・)
theorem
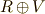 の元は,全て異なる同値類に分類されます.
の元は,全て異なる同値類に分類されます.
proof
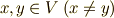 に対し,
に対し, 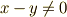 ,
, 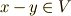 ,
, 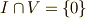 より,
より, 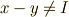 が示されます.
が示されます. 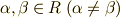 に対しても,全く同様にして
に対しても,全く同様にして 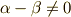 ,
, 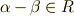 ,
,  より,
より, 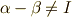 が示されます.■
が示されます.■
イデアルによる商代数で二つの元が同値だとは, 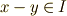 の意味であることを思い出してください.( 剰余類2 を参考にして下さい.)これより,例えば
の意味であることを思い出してください.( 剰余類2 を参考にして下さい.)これより,例えば 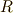 や
や 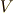 の元を
の元を 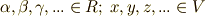 のように表わせば,
のように表わせば,  は,これらが含まれる類を全て別々に持つということです.
は,これらが含まれる類を全て別々に持つということです.
![E(V)=T(V)/I = \{ [\alpha ],[\beta ], [\gamma ],...,[x],[y],[z],....\}](./b5ece64cd2326b1d6093a319f78afa9b.png)
もちろん, 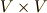 以上の元
以上の元 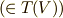 がどのような類に入るかはまだ明らかではありませんが,
がどのような類に入るかはまだ明らかではありませんが, 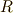 と
と 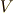 に関しては,
に関しては, 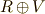 と
と 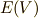 の元に 一対一対応がつく ことが分かりました.とりあえず一安心です.先に進む前に,もう一度ここまでの議論をよく確認して下さい.
の元に 一対一対応がつく ことが分かりました.とりあえず一安心です.先に進む前に,もう一度ここまでの議論をよく確認して下さい.
外積代数の分解
テンソル空間 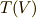 から
から 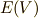 への写像を
への写像を 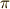 としましょう.まず,
としましょう.まず, 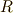 や
や 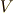 の元の対応は一対一です.
の元の対応は一対一です.
![\pi : \ \pi (\alpha ) \ \ \longmapsto \ \ [\alpha] \in E(V) \ \ (\forall \alpha \in R)](./7bbea5cae095e65abff395048219fcbc.png)
![\pi : \ \pi (x ) \ \ \longmapsto \ \ [x] \in E(V) \ \ (\forall x \in V)](./bfe51e5198c819b6dcd20e740cfe6e7d.png)
これにより, 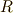 と
と  ,
, 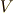 と
と 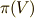 を同一視することが出来ます.
を同一視することが出来ます.
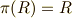

さて,問題は 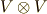 以上の階数のテンソルです.テンソル積
以上の階数のテンソルです.テンソル積 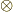 を
を 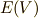 に入っている乗法(記号は
に入っている乗法(記号は 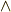 で表わすことにします)に対応させ,次のように考えます.
で表わすことにします)に対応させ,次のように考えます.
![\pi (x \otimes y) = [x] \land [y] = x \land y \ \ (x,y \in V)](./3cdd72944e40b8cd6b746504e9aa4fd3.png)
これより,ベクトル空間 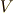 全体の写像は次のように書けるでしょう.
全体の写像は次のように書けるでしょう.
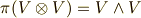
より高階のテンソル空間についても,同様とします.

これらの結果より, 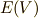 は次のように部分ベクトル空間の和として表わせる構造だということが分かりました.
は次のように部分ベクトル空間の和として表わせる構造だということが分かりました.
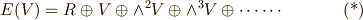
右辺に出て来る各外積空間 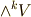 の基底は独立で,左辺を直和分解の形で書くことが出来ます.この続きは イデアルで外積代数を入れる3 で考えます.
の基底は独立で,左辺を直和分解の形で書くことが出来ます.この続きは イデアルで外積代数を入れる3 で考えます.