面積素と微分形式
曲面 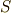 が
が  で与えられているとき,その面積素は次式で与えられるのでした.面積素というのは,面積分するときに出て来る
で与えられているとき,その面積素は次式で与えられるのでした.面積素というのは,面積分するときに出て来る 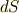 ってやつです.ただし,
ってやつです.ただし, 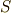 の法線ベクトルは
の法線ベクトルは 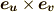 と同じ向きを正とします.( 面積素に関して補足 も参照して下さい.)
と同じ向きを正とします.( 面積素に関して補足 も参照して下さい.)
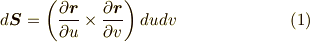
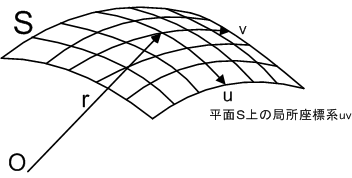
滑らかな曲面上の領域が,上図のように二つの独立なパラメーターで表わせるという事は直観的に了承して,先に進むことにしましょう.
| [*] | いま考えている点の近傍で曲面は滑らかだとしています.曲面上の領域が二つのパラメーターで表わせるという事をもう少し正確に言えば,この曲面上のどの点の近傍も,二次元ユークリッド空間と同じだと見ることが出来るということです.(このような曲面を,二次元多様体と呼びます.)ここでは,あまり深入りしませんが,詳しくは, 多様体 カテゴリーを参考にして下さい. |
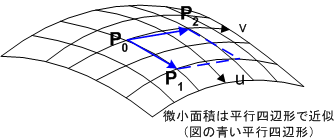
曲面  上の一点
上の一点 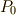 のまわりに微小面積を取ることを考えます.点
のまわりに微小面積を取ることを考えます.点 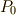 の位置ベクトルを
の位置ベクトルを  とし,上図のように
とし,上図のように  が
が  とともに変化する方向(
とともに変化する方向( 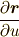 の方向)に
の方向)に 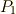 ,
,  が
が  とともに変化する方向(
とともに変化する方向(  の方向)に
の方向)に 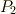 をとります.曲面は本当は曲がっているわけですが,いま微小量を考えているので,
をとります.曲面は本当は曲がっているわけですが,いま微小量を考えているので, 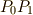 や
や  はほぼ直線とみなし,
はほぼ直線とみなし, 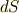 として,
として, 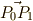 と
と 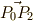 が張る平行四辺形を考えます.
が張る平行四辺形を考えます.
![d\bm{S} &= \vec{P_{0}P_{1}} \times \vec{P_{0}P_{2}} \\&= (\vec{P_{1}}- \vec{P_{0}}) \times (\vec{P_{2}} - \vec{P_{0}}) \\ & = \left[ \left( \bm{r} + \frac{\partial \bm{r}}{\partial u}du \right) - \bm{r} \right] \times \left[ \left( \bm{r} + \frac{\partial \bm{r}}{\partial v}dv \right) - \bm{r} \right] \\ & = \frac{\partial \bm{r}}{\partial u}du \times \frac{\partial \bm{r}}{\partial v}dv \\ & =\left( \frac{\partial \bm{r}}{\partial u} \times \frac{\partial \bm{r}}{\partial v} \right) dudv \tag{2}](./f1992b0116f2f1673f7f4a2d5286924e.png)
偏導関数をいちいち分数の形に書くのは面倒なので,以後,微分変数を添字にして,例えば 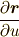 を
を 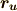 のように略記することにします.
のように略記することにします.
| [†] | 細かいことを言えば,曲面上の微小面積は曲率を持っていて,平行四辺形による表現はあくまで近似のはずです. 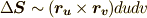 .そして, .そして, 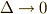 の極限において初めて, の極限において初めて, 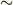 が が  になります.(つまり,曲率を持った面積素と平行四辺形の差が になります.(つまり,曲率を持った面積素と平行四辺形の差が  に収束します.)このような二段階で, に収束します.)このような二段階で, 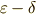 論法を使って示すのが正確ですが,式 論法を使って示すのが正確ですが,式 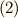 は少しいい加減に最初から『面積素 は少しいい加減に最初から『面積素  平行四辺形』として計算してしまいました.厳密に考えたい人は,詳しい教科書をあたって下さい. 平行四辺形』として計算してしまいました.厳密に考えたい人は,詳しい教科書をあたって下さい. |
蛇足ですが,曲面の第一基本量と呼ばれる量, 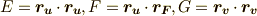 を使えば,式
を使えば,式 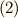 を次のように簡単に書くこともできます.
を次のように簡単に書くこともできます.
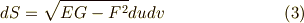
ヤコビアンと面積素
曲面  を表わすベクトル方程式
を表わすベクトル方程式 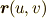 を用いて,式
を用いて,式 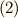 もしくは
もしくは 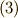 の形で面積素
の形で面積素 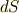 を表現することが出来ました.曲面上のパラメーター二つで表わすのは簡潔で良いですが,応用上の便宜も考えて,次のようにデカルト座標系
を表現することが出来ました.曲面上のパラメーター二つで表わすのは簡潔で良いですが,応用上の便宜も考えて,次のようにデカルト座標系 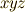 で
で 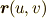 を表現することも考えてみましょう.
を表現することも考えてみましょう.
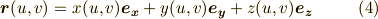
これを使うと,式 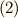 は次のようになります.
は次のようになります.
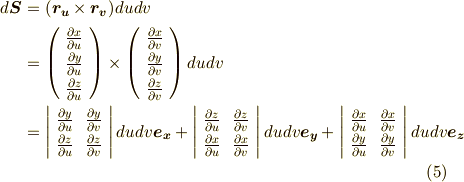
なんだか,行列式がたくさん出てきてエライことになってますが,これらは  のうちの二変数から
のうちの二変数から 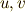 へ座標変換する際の ヤコビアン になっていることが分かるかと思います.(ヤコビアンを忘れてしまっている人は,やばいですよ.すぐに復習して下さい!)
へ座標変換する際の ヤコビアン になっていることが分かるかと思います.(ヤコビアンを忘れてしまっている人は,やばいですよ.すぐに復習して下さい!)
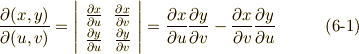
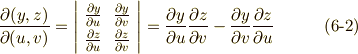
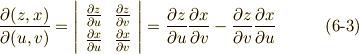
この表記を使って  をもう一度書き直せば,次のようになります.
をもう一度書き直せば,次のようになります.
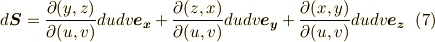
ずいぶん,すっきりしました.
ヤコビアンと微分形式
前セクションでは, 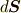 を
を 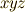 成分に分解してみました.さて,式
成分に分解してみました.さて,式 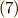 から,第一成分の
から,第一成分の 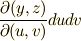 だけを例に取って,さらに座標変換について考えてみましょう.このヤコビアンの符号には正負があり,
だけを例に取って,さらに座標変換について考えてみましょう.このヤコビアンの符号には正負があり, 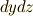 と
と 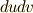 を次式のように関係づけます.
を次式のように関係づけます.
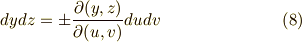
特に,正の符号を取る変換を 向きを保つ座標変換 と呼びます.座標系の向きを直観的に理解しやすい例は三次元直交座標で,右手系を右手系に,もしくは左手系を左手系に保つ座標変換が,正のヤコビアンによって表わされることになります.(後で,この話に戻って来ますから,ヤコビアンの符号と,座標変換の向きという話を覚えておいて下さい.)
それにしても,符号が  となっているのは,いかにも面倒くさいですねぇ.
となっているのは,いかにも面倒くさいですねぇ.
ヤコビアンの性質
ここで,一般にヤコビアンの持つ性質を考えて見たいと思います. 行列式の性質 により,ヤコビアンは次の性質を持つことが分かると思います.
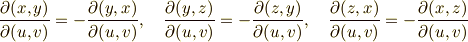
Important
ヤコビアンの符号は,行か列を入れ替えると反転します.
また,次の性質もあることが言えます.
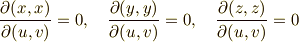
Important
同じ行(もしくは同じ列)があると,ヤコビアンは  になります.
になります.
座標の向きとの関係
このセクションの最初に少し考えた,座標変換で向きを保つ,という話に戻ります.二つの座標軸を入れ替える座標変換のヤコビアンは負になりますので,向きを保ちません.このことは,例えば次のような座標変換のヤコビアンが 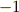 になることを見れば,明らかでしょう.
になることを見れば,明らかでしょう.
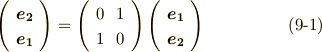
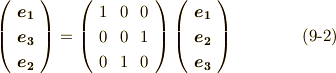
このように,『座標軸を入れ替える』という操作は,実はヤコビ行列の行(もしくは列)を入れ替える操作に等しくなります.式 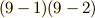 で考えたヤコビ行列の行列式が,単位行列の行を一回入れ替えることで得られることを確認して下さい.座標軸の入れ替えも,二回行えばヤコビアンの符号は元に戻ります.そこで,『座標変換が向きを保つか』という問題は,考えているヤコビ行列が,向きを保つ座標変換(例えば単位行列で表わされる恒等変換)の表現行列の行(もしくは列)を,何回入れ替えたものなのか,より具体的には, 偶数回入れ替えたか奇数回入れ替えたか という問題に帰着します.
で考えたヤコビ行列の行列式が,単位行列の行を一回入れ替えることで得られることを確認して下さい.座標軸の入れ替えも,二回行えばヤコビアンの符号は元に戻ります.そこで,『座標変換が向きを保つか』という問題は,考えているヤコビ行列が,向きを保つ座標変換(例えば単位行列で表わされる恒等変換)の表現行列の行(もしくは列)を,何回入れ替えたものなのか,より具体的には, 偶数回入れ替えたか奇数回入れ替えたか という問題に帰着します.
なぜ,『向きを保つ』という問題にこだわっているのか,少し面倒臭く感じている人がいるかも知れません.私達が 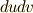 とか
とか 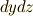 という面積素を考えているのは,それを使って面積分をしたい,という目論見が背後にあるからです.そして,面積分においては 曲面の向き がとても重要でした.(例えば ガウスの発散定理 を復習してみて下さい.)私達は,曲面上の領域を表わすのに,自由自在に座標変換したい訳ですが,このとき,面積素の面積だけでなく,曲面の向き(つまり曲面の法線ベクトルの方向)も自然に保つような座標変換の体系を考えたいのです.これが,向きにこだわっている動機です.(だって,積分のたびに向きをごちゃごちゃ考えるのは面倒ですよね.)
という面積素を考えているのは,それを使って面積分をしたい,という目論見が背後にあるからです.そして,面積分においては 曲面の向き がとても重要でした.(例えば ガウスの発散定理 を復習してみて下さい.)私達は,曲面上の領域を表わすのに,自由自在に座標変換したい訳ですが,このとき,面積素の面積だけでなく,曲面の向き(つまり曲面の法線ベクトルの方向)も自然に保つような座標変換の体系を考えたいのです.これが,向きにこだわっている動機です.(だって,積分のたびに向きをごちゃごちゃ考えるのは面倒ですよね.)
そこで,いっそ式 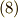 を次のように書いてしまえば便利でしょう.
を次のように書いてしまえば便利でしょう.
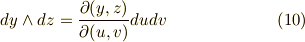
いきなりウェッジ積が出てきましたが,『積の順序を(奇数回)変えれば符号が変わる』というウェッジ積の性質と,『二つの行や列を(奇数回)入れ替えれば符号が変わる』というヤコビアンの性質が,見事にマッチしている訳です.これで,最初に基準となる  座標系の向きさえ決めておけば(つまり,曲面の表・裏を最初に決めるということです.どちらが表でどちらが裏か,という決定には任意性があります),その後は座標変換に伴う向きの変化を気にしなくて済むことになりますo(^ー^)o.
座標系の向きさえ決めておけば(つまり,曲面の表・裏を最初に決めるということです.どちらが表でどちらが裏か,という決定には任意性があります),その後は座標変換に伴う向きの変化を気にしなくて済むことになりますo(^ー^)o.
ヤコビアンの二番目の性質,『同じ行や列があると零になる』という性質ですが,これもウェッジ積の『同じもののウェッジ積は零になる』という性質 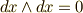 に,見事にマッチしています.どうやら,二次微分形式を使うと, 向きに関するヤコビアンの性質を織り込んだ面積素 を考えることができそうです.
に,見事にマッチしています.どうやら,二次微分形式を使うと, 向きに関するヤコビアンの性質を織り込んだ面積素 を考えることができそうです.
Important
二次微分形式は,曲面の向き(表・裏)に関する情報も織り込んだ面積素だと考えても良いです.
これは,面積分で重宝しそうですね!微分形式を使えば,次のような表現が可能です.
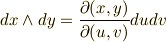
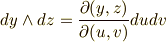
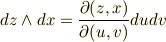
これを使って,式  を次のように簡単な形にできます.もう一度,式
を次のように簡単な形にできます.もう一度,式  と比べてみて下さい.
と比べてみて下さい.
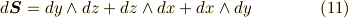
例えば,ガウスの発散定理に出てくる面積分は,式 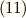 を使って表現すると次のようになります.
を使って表現すると次のようになります.
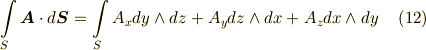
ここで式  の右辺は二次微分形式になっていることが分かると思います.図形的に,式
の右辺は二次微分形式になっていることが分かると思います.図形的に,式  は『単位時間あたりに面
は『単位時間あたりに面 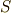 を通過する
を通過する  の 流量 』という意味を持っていましたが,これはそのまま微分二形式の物理的意味として重要な解釈です.
の 流量 』という意味を持っていましたが,これはそのまま微分二形式の物理的意味として重要な解釈です.
| [‡] | 代数的に,ベクトル空間→テンソル空間→外積代数と勉強して来た人は,外積空間なんていうものは抽象的思考の産物で,実際の役に立たないのではないかと感じていたかも知れません.(実際,グラスマン(    )が外積代数を考え出したときは,これが何の役に立つのか,誰も分かりませんでした.)この記事では曲面の向きと面積分という観点だけから微分形式を見たわけですが,外積代数の基底を )が外積代数を考え出したときは,これが何の役に立つのか,誰も分かりませんでした.)この記事では曲面の向きと面積分という観点だけから微分形式を見たわけですが,外積代数の基底を 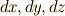 にしてみただけで,『曲面の向き』『座標変換』『面積分の向き』といった(面倒な)話題が,綺麗に,微分形式の表現に収まってしまったのを見ました.外積代数も,やはり役に立たない抽象思考の産物では無かったわけです.なんと言っても,微分形式は美しいです. にしてみただけで,『曲面の向き』『座標変換』『面積分の向き』といった(面倒な)話題が,綺麗に,微分形式の表現に収まってしまったのを見ました.外積代数も,やはり役に立たない抽象思考の産物では無かったわけです.なんと言っても,微分形式は美しいです. |