置換の計算
前節 対称群 に置換の計算が出てきましたが,あまり馴染みがない人のために置換の計算規則を補足します.分かっている人は,この記事は飛ばしてください.内容は 対称群 の説明とも重複します.
以下の説明には,主に4文字の置換を使いますが,もちろん一般に  文字の置換でも同じ議論がなりたちます.
文字の置換でも同じ議論がなりたちます.
括弧の意味
置換を次のように括弧で表わす表記法は既に見ました.
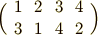
この記号は,上の列の文字を下の列の文字に変換する,というように解釈します.上の例は『 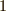 を
を 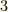 に,
に, 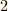 を
を 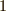 に,
に, 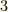 を
を 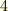 に,
に, 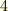 を
を 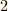 にに変える』という意味です.
にに変える』という意味です.
まず,これは 行列ではありません .
巡回置換の略記法
四つの文字 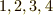 のうち,
のうち, 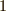 と
と 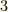 だけを入れ換える置換は
だけを入れ換える置換は 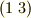 のように略記できます.意味は
のように略記できます.意味は 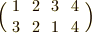 と同じです.
と同じです.
また,置換を繰り返して一巡する場合,これを巡回置換と呼びます.図で見ると分かりやすいのですが,一巡するとは,次々に置換を繰り返した結果,また最初の文字にどこかで戻り,そこで置換の連鎖が閉じるような置換列のことです.
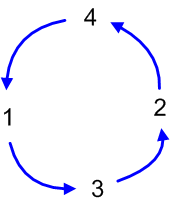
例えば,この図の例では『 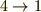 ,
, 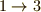 ,
, 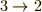 ,
, 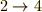 』という具合に置換が巡回しています.これをきちんと二列に
』という具合に置換が巡回しています.これをきちんと二列に 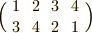 のように書いても同じことです.
のように書いても同じことです.
巡回置換は 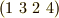 のように略記することで出来ます.最初の文字から順番にずらして
のように略記することで出来ます.最初の文字から順番にずらして 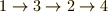 のように読みます.最後の文字だけは最初に文字に戻すようにします.
のように読みます.最後の文字だけは最初に文字に戻すようにします.
当然のことながら, 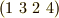 ,
, 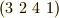 ,
, 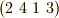 ,
, 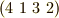 はどれも同じ巡回置換を表わしています.
はどれも同じ巡回置換を表わしています.
| [*] | 互換も巡回置換の一つです. |
| [†] | 一番単純な巡回置換 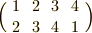 が が 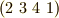 と書けることからか,たまに巡回置換の略記法を『二列に書いた置換の記号の下の列だけを書く』と勘違いしている人がいます.そのような勘違いに基づいて書かれたサイトもありますので注意してください. と書けることからか,たまに巡回置換の略記法を『二列に書いた置換の記号の下の列だけを書く』と勘違いしている人がいます.そのような勘違いに基づいて書かれたサイトもありますので注意してください. |
置換の積
連続的に置換を重ねていくことを,置換の積といいます.例えば次のように書きます.
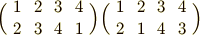
ここで重要なのは, 置換の操作が一般には非可換 だという点です.つまり,この置換を対象物に左から作用させるのか,右から作用させるのかで結果が変わってくることに注意しなければなりません.
もしも,この固まりを左から掛ける場合(通常は,左からの作用を考える場合が多いです),上の例では 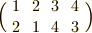 が最初に作用しますので,まず
が最初に作用しますので,まず 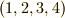 が
が 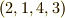 に変わります.その次に
に変わります.その次に 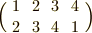 が作用するので,
が作用するので, 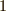 は
は 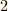 に,
に, 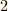 は
は 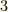 に,
に, 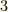 は
は 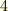 に,
に, 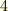 は
は 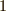 に移され,
に移され, 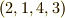 は
は 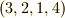 になります.よって次のように書けます.
になります.よって次のように書けます.
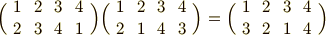
もし,右からの作用を考える場合は 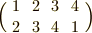 が先に作用することになります.結果は次のようになることを,自分で確認してみてください.
が先に作用することになります.結果は次のようになることを,自分で確認してみてください.
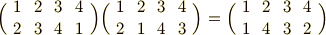
| [‡] | 『左から』『右から』という言葉で混乱する人がいるかも知れないので補足しておきます.例えば行列の積  がベクトル がベクトル  に作用する場合,左から作用する( に作用する場合,左から作用する( 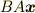 )なら最初に )なら最初に 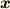 に作用するのは に作用するのは 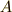 です.逆に右側から作用する( です.逆に右側から作用する( 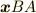 )なら,最初に )なら,最初に 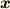 に作用するのは に作用するのは 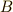 です. です. 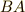 の見かけの左右と作用する順番は逆ですので注意してください.群の元が作用する,という意味は 群が集合の上で働くということ で詳しく勉強します. の見かけの左右と作用する順番は逆ですので注意してください.群の元が作用する,という意味は 群が集合の上で働くということ で詳しく勉強します. |
| [§] | 幾つもの置換の積を取る場合には,紙の上で上から下に向かうように縦に置換の記号を書いていき,上から順番に操作していくようにすると間違いが少なくて済みます. |
単位置換,逆置換
単位置換(恒等置換とも言う)は 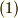 のように書くこともあります.
のように書くこともあります.  を使っても構いません.
を使っても構いません.
逆置換は,上下の二列を入れ換えれば得られます.例えば次のような具合です.
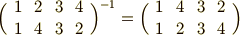
互換は二乗すれば元に戻りますから,互換の逆元は自分自身だと言えます.
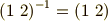
互いに素な置換
5文字の置換で,次のようなものを考えてみます.
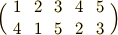
よくみると,この置換は 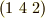 と
と 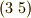 という二つの巡回置換からなっており,それぞれの巡回置換は,お互いに関係のない文字の間だけで行われていることが分かります.
という二つの巡回置換からなっており,それぞれの巡回置換は,お互いに関係のない文字の間だけで行われていることが分かります.
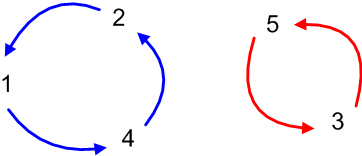
二つの巡回置換が,こうした家庭内離婚のような状態にあることを『互いに素』と言います.互いに素な巡回置換の積は可換です.