中心化群
中心化群の定義には,ここまでに勉強してきた,共役,共役類,軌道,中心,固定部分群といった概念が全て必要になります.何となく曖昧な部分がある人は,先に復習しておきましょう.
中心化群の定義
群 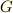 のある元
のある元  を考えます.
を考えます.  に対し,
に対し, 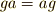 を満たす
を満たす 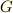 の元を全て集めた集合は群になり,これを
の元を全て集めた集合は群になり,これを  の中心化群
の中心化群 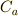 と呼びます.
と呼びます.
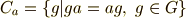
『中心化群とは,群のある元に対し, 群自身への共役作用を考えるときの固定部分群である 』と言い換えることもできるでしょう.( 共役類 , 群が集合の上で働くということ , 固定部分群 を参照して下さい.)
中心化群に関しては,次の定理が重要です.
theorem
群 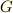 の元
の元  に対し,
に対し, 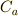 を
を  の中心化群,
の中心化群, 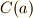 を
を  の共役類(軌道)とすると,位数に関して
の共役類(軌道)とすると,位数に関して 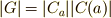 がなりたちます.
がなりたちます.
群の位数 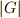 は定数ですから,
は定数ですから,  の中心化群が大きければ,
の中心化群が大きければ,  の共役類は小さくなり,逆に
の共役類は小さくなり,逆に  の中心化群が小さいと,
の中心化群が小さいと,  の共役類が大きくなるということです.中心化群は固定部分群の特殊な場合ですから, 固定部分群 に出てきた式
の共役類が大きくなるということです.中心化群は固定部分群の特殊な場合ですから, 固定部分群 に出てきた式 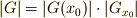 などと比較して,もう一度頭を整理しましょう.
などと比較して,もう一度頭を整理しましょう.
部分集合の中心化群
上の定義では,ある一つの元  に対し,
に対し,  に共役な元を全て集めたものを「元
に共役な元を全て集めたものを「元  の中心化群」としました.同様に,この定義を拡張し,群
の中心化群」としました.同様に,この定義を拡張し,群 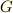 のある部分集合
のある部分集合 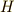 に対し,
に対し, 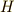 に属する全ての元と共役な
に属する全ての元と共役な 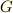 の元を全て集めた集合を「部分集合
の元を全て集めた集合を「部分集合 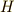 の中心化群」と定義できます.
の中心化群」と定義できます.
例1
三次の対称群 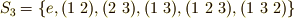 で,例えば
で,例えば 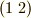 の中心化群を求めてみましょう.
の中心化群を求めてみましょう.
求めたいのは, 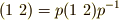 を満たす全ての
を満たす全ての 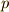 です.順番に全部試してみても,計算はすぐに済みますが,結果としては,
です.順番に全部試してみても,計算はすぐに済みますが,結果としては, 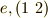 の二つが求まります.よって,
の二つが求まります.よって, 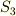 の
の 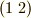 に関する中心化群は
に関する中心化群は 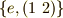 と決まります.確かに
と決まります.確かに 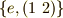 だけで群になっていますね.
だけで群になっていますね.
例2
点 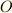 を中心とする回転全てからなる群を考えます.このとき,
を中心とする回転全てからなる群を考えます.このとき,  軸を中心としたある回転
軸を中心としたある回転 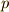 (静止と
(静止と 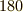 度回転を除く)に関する中心化群はどのような回転の集まりになるでしょうか.
度回転を除く)に関する中心化群はどのような回転の集まりになるでしょうか.
一般に,異なる軸に関する回転操作は非可換でしたので, 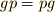 を満たすような元
を満たすような元 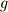 もやはり
もやはり  軸回りの回転であると考えられます.逆に,
軸回りの回転であると考えられます.逆に, 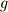 が
が  軸回りの回転を表わす元ならば,
軸回りの回転を表わす元ならば, 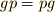 を満たします.
を満たします. 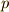 の中心化群は,
の中心化群は,  軸回りの回転全て(静止と
軸回りの回転全て(静止と 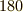 度回転も含む)からなるものです.
度回転も含む)からなるものです.
発展:
すぐに重要な訳ではありませんが, 群の中心 の記事で軽く紹介した 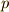 群には,興味深い定理がなりたつので,証明とともに紹介しておきます.証明の途中で中心化群を利用します.
群には,興味深い定理がなりたつので,証明とともに紹介しておきます.証明の途中で中心化群を利用します.
theorem
位数が素数の平方である有限群は,可換群になります.
proof
中心 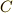 は群
は群 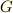 の部分群ですから,中心の位数は,群の位数
の部分群ですから,中心の位数は,群の位数 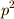 の約数になっているはずです. 群の中心 の「群の位数と中心」のセクションで紹介した定理により,中心
の約数になっているはずです. 群の中心 の「群の位数と中心」のセクションで紹介した定理により,中心 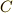 には二つ以上の元がありますから,中心の位数として可能なのは
には二つ以上の元がありますから,中心の位数として可能なのは 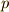 か
か 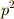 だけです.
だけです. 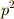 のときは,中心は群
のときは,中心は群 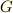 そのものということであり,これは群の全ての元が演算に関して交換可能,すなわち可換群であるという主張です.一方,中心の位数が
そのものということであり,これは群の全ての元が演算に関して交換可能,すなわち可換群であるという主張です.一方,中心の位数が 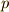 のときは,
のときは, 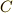 に含まれない
に含まれない 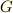 の元を一つ(仮に
の元を一つ(仮に  とします)取ると,
とします)取ると,  の中心化群は
の中心化群は 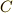 を含み,かつ
を含み,かつ  の累乗をも含みますので,この中心化群の位数はは中心の位数
の累乗をも含みますので,この中心化群の位数はは中心の位数 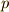 よりも大きくなるはずです.すると中心化群の位数は
よりも大きくなるはずです.すると中心化群の位数は 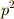 ということになりますが,この場合,中心化群が群
ということになりますが,この場合,中心化群が群 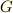 そのものとなり,
そのものとなり,  が中心
が中心 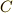 に含まれてしまうことになりますので,これは矛盾です.よって中心の位数が
に含まれてしまうことになりますので,これは矛盾です.よって中心の位数が 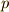 ということはありえず,p群の中心は常に群そのものと一致し,可換群になりことが分かりました.■
ということはありえず,p群の中心は常に群そのものと一致し,可換群になりことが分かりました.■