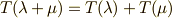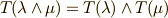外微分の座標不変性
外微分には,『座標変換しても不変である』という著しい特徴があります.微分という演算は,普通は『ある向きに沿って関数の変化を調べる』という操作ですから,向きによって話が変わってきます.ところが,私達が考えている外微分という操作は,座標系の取り方によらない,という言うのですね.これは驚くべき性質です.(これは,外微分が普通の微分ではなくて,全微分を拡張したものだからです.)実は,微分形式の威力が真に発揮される場面は,外微分によって定式化された微分形式が,座標系の取り方とは独立の関係式を鮮やかに記述する時です.
既に 外微分 の最後で関数の全微分(一次微分形式)の座標不変性は証明しました.わざわざ書くほどのことは無いかも知れませんが,大事なことなので,もう一度,定理として掲げておきます.
theorem
零次微分形式(関数)の外微分(一次微分形式)は座標不変です.
この記事では,より高次の外微分の座標不変性を検証します.
二次微分形式の不変性
一次微分形式 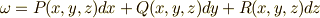 が座標の取り方によらないということでしたので,
が座標の取り方によらないということでしたので,  と異なる取り方の座標系
と異なる取り方の座標系 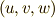 に対し,次式が成り立ちます.(
に対し,次式が成り立ちます.(  上の外積代数を考えています.)
上の外積代数を考えています.)
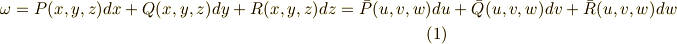
ただし,式中, 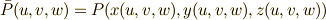 等としました.(同じ関数なのですが,変数変換をすると関数の形が変わるので,上にバーをつけました.)式
等としました.(同じ関数なのですが,変数変換をすると関数の形が変わるので,上にバーをつけました.)式  の両辺の外微分を取ってみましょう.式
の両辺の外微分を取ってみましょう.式  の左辺は
の左辺は 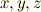 だけで記述されていますし,右辺は
だけで記述されていますし,右辺は 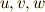 だけで記述されています.ということは,左辺の外微分は
だけで記述されています.ということは,左辺の外微分は 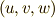 とは無関係に
とは無関係に  となり,右辺の外微分は
となり,右辺の外微分は 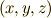 とは無関係に
とは無関係に 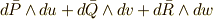 となります.(外微分を取る,という操作自体に,文字の名前は関係ないわけです.)
となります.(外微分を取る,という操作自体に,文字の名前は関係ないわけです.)
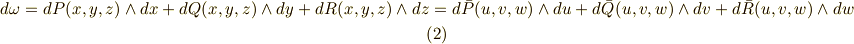
ここで 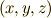 と
と 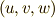 は,十分滑らかで微分可能な関数によって,互いに関係づけられている別々な座標系だとしています.このとき,式
は,十分滑らかで微分可能な関数によって,互いに関係づけられている別々な座標系だとしています.このとき,式  は,二次微分形式が座標系の取り方によらないことを意味していると言えます.
は,二次微分形式が座標系の取り方によらないことを意味していると言えます.
| [*] | ここで,きちっとした証明というよりは,文字の置き換えだけで座標不変性を示しましたが,右辺で  の外微分という意味での の外微分という意味での 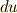 と,微分形式における基底としての と,微分形式における基底としての 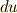 とが混同して用いられたことに抵抗を感じた人があると思います.関数 とが混同して用いられたことに抵抗を感じた人があると思います.関数  の外微分を取れば, の外微分を取れば,  となりますが,これを外微分と見ても良いし,基底の変換だと見ることも出来ます.(分かりにくい人は, となりますが,これを外微分と見ても良いし,基底の変換だと見ることも出来ます.(分かりにくい人は, 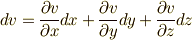 や や  と並べ,三行三列の行列の形に整理すれば(そのような行列をヤコビ行列と呼ぶのでした), と並べ,三行三列の行列の形に整理すれば(そのような行列をヤコビ行列と呼ぶのでした),  から から 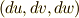 への座標変換という意味がはっきりするのではないでしょうか.)つまり, への座標変換という意味がはっきりするのではないでしょうか.)つまり,  の外微分としての の外微分としての 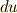 と,微分形式における外積空間の基底としての と,微分形式における外積空間の基底としての 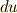 は『全く同じもの』と見ても良いのです.この点は,今まであまり明示的に検証せずに,外微分や外積空間を議論してきてしまいましたが,きちんと意味を理解すべき点です.積分計算を初めて勉強したとき, は『全く同じもの』と見ても良いのです.この点は,今まであまり明示的に検証せずに,外微分や外積空間を議論してきてしまいましたが,きちんと意味を理解すべき点です.積分計算を初めて勉強したとき, 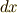 等の記号は,あまり躍動感のある意味を持っているとは思えませんでした.しかし,いまベクトル空間の基底という意味や,外微分という意味も与えられ,俄然,解析学と幾何学が融合してきたわけです. 等の記号は,あまり躍動感のある意味を持っているとは思えませんでした.しかし,いまベクトル空間の基底という意味や,外微分という意味も与えられ,俄然,解析学と幾何学が融合してきたわけです.  の外微分としての の外微分としての 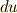 とベクトル空間の基底としての とベクトル空間の基底としての 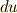 が同じだ,という事実に,解析学と幾何学の融合と言うドラマを感じ取って下さい.微分幾何学の醍醐味です. が同じだ,という事実に,解析学と幾何学の融合と言うドラマを感じ取って下さい.微分幾何学の醍醐味です. |
theorem
一次微分形式の外微分(二次微分形式)も座標不変です.
一般の次数の微分形式に対し,外微分が座標不変であることを次のセクションで示しますが,証明が面倒です.まずは『外微分は座標不変なんだ!』という結果だけとりあえず受け容れて,次の記事に進むのも良いと思います.
一般の場合
高次の微分形式一般について,もっと直接的に座標変換を使って外微分の座標不変性を示しておきます. 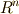 の座標を
の座標を 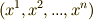 とし,
とし, 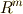 の座標を
の座標を 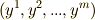 とします.いま,
とします.いま, 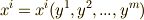 の形で,
の形で, 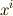 系から
系から 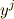 系への写像を使って表現できるとします.この写像は,何回でも微分可能な関数だとし,
系への写像を使って表現できるとします.この写像は,何回でも微分可能な関数だとし, 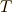 で表わします.
で表わします.
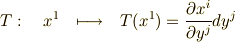
このような写像が, 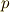 次微分形式
次微分形式 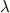 ,
, 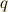 次微分形式
次微分形式 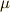 に作用するとき,次のような性質が言えます.
に作用するとき,次のような性質が言えます.
性質  は明らかでしょう.性質
は明らかでしょう.性質 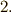 は次のように証明します.
は次のように証明します.
proof
写像を表わす行列を 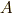 とし,
とし, 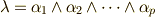 ,
, 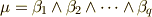 とします.
とします. 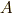 が
が 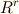 を
を 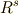 に移す変換だとすれば,
に移す変換だとすれば,  を
を 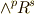 に移す変換は
に移す変換は 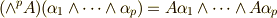 と書くことが出来ます.(これを『
と書くことが出来ます.(これを『 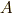 の外積
の外積 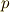 乗』と呼びます.)いま,
乗』と呼びます.)いま, 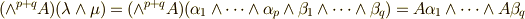 と書けます.この右辺は
と書けます.この右辺は 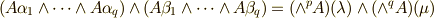 と変形できますので,結局
と変形できますので,結局 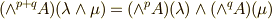 が言えます.
が言えます.  の
の 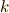 次微分方形式への作用(一次変換なので行列で表わせる)を
次微分方形式への作用(一次変換なので行列で表わせる)を 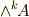 と表現すれば,性質
と表現すれば,性質 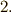 が示されます.■
が示されます.■
性質 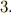 が大事です.これは帰納法で証明します.
が大事です.これは帰納法で証明します.
proof
まず零次微分形式 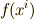 に対して,
に対して, 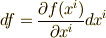 が成り立ちますので,
が成り立ちますので, 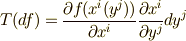 が言えます
が言えます 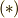 .
. 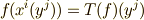 と置けば,式
と置けば,式 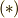 は
は 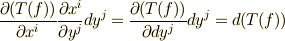 と変形でき(微分のチェイン・ルール),性質
と変形でき(微分のチェイン・ルール),性質 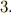 が成り立っています.さて,次に一般に
が成り立っています.さて,次に一般に  次微分形式について性質
次微分形式について性質 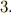 が言えると仮定します.
が言えると仮定します.  を
を  次微分形式とすれば,
次微分形式とすれば, 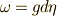 の形の
の形の 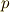 次微分形式が一つ決まります.一般の
次微分形式が一つ決まります.一般の 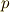 次微分形式は,この
次微分形式は,この 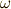 と同じ形の元の一次結合として表わせますので,この
と同じ形の元の一次結合として表わせますので,この 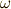 についてだけ定理を示せば十分です.いま,性質
についてだけ定理を示せば十分です.いま,性質 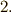 より
より 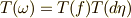 が言えますが,仮定より,さらに
が言えますが,仮定より,さらに  が言えます.これより,両辺の外微分を取って
が言えます.これより,両辺の外微分を取って 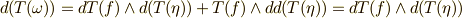 を得ます.(
を得ます.( 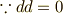 )一方,
)一方, 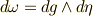 より,
より, 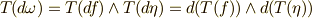 ですから,
ですから, 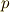 次微分形式についても
次微分形式についても 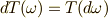 が言えました.■
が言えました.■
さて,いま示した性質 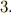 ですが,これは式をそのまま日本語にすれば,『外微分してから座標変換しても,座標変換してから外微分しても同じだということです.』ということになります.これは『外微分が座標変換によらない』という意味だと考えても良いですよね.これが,外微分の最も特徴的な性質です.
ですが,これは式をそのまま日本語にすれば,『外微分してから座標変換しても,座標変換してから外微分しても同じだということです.』ということになります.これは『外微分が座標変換によらない』という意味だと考えても良いですよね.これが,外微分の最も特徴的な性質です.
theorem
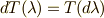
証明は面倒でしたが,実は,この結果を覚えておくと,あとで 微分形式の引き戻し という話や, 微分形式の積分 といった話が簡単に分かります.また,今は三次元ユークリッド空間上だけで微分形式を考えていますが,あとで,より一般に多様体と呼ぶ空間上にまで微分形式の定義を拡張するとき,外微分のこの性質が,本質的に重要になってきます.
カルタン
微分形式を最初に使い始めたのは,フランスの数学者エリー・カルタン(  )です.息子のアンリ・カルタン(
)です.息子のアンリ・カルタン(  )も有名な数学者なので,カルタンを呼ぶ場合にはファーストネームも一緒に呼んで,区別することが多いようです.微分形式の父・エリー・カルタンですが,外積代数の枠組みに外微分を組み合わせるというアイデアは,座標系によらない形で微分方程式を記述しようという試みから最初は始まったということです.
)も有名な数学者なので,カルタンを呼ぶ場合にはファーストネームも一緒に呼んで,区別することが多いようです.微分形式の父・エリー・カルタンですが,外積代数の枠組みに外微分を組み合わせるというアイデアは,座標系によらない形で微分方程式を記述しようという試みから最初は始まったということです.

カルタン家の子供はみな楽器を弾き,音楽あふれる一家だった.息子に数学を押し付けることもなく,子供達はのびのび育った.
量子力学で必須となるスピノールの理論を創始したのもエリー・カルタンです.エリー・カルタンは微分幾何やリー代数の分野に膨大な貢献をし,既知の話題にも,多くの現代的視点を与えました.特に微分形式の理論は,ほとんど全て一人で作り上げたものです.