外微分
三次元ユークリッド空間 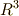 上の外積代数を考えると,微分形式として次の
上の外積代数を考えると,微分形式として次の 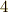 つを定義できました.
つを定義できました.
【零次微分形式】
ただの関数. 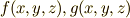 など.
など.
【一次微分形式】
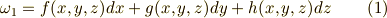
【二次微分形式】
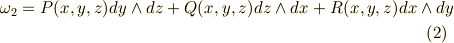
【三次微分形式】
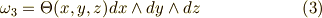
それぞれ, 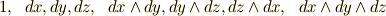 を基底とするベクトルの形になっていることを,もう一度確認して下さい.(零次微分形式はスカラーに相当.)さて,基底の次数別に何次微分形式などと呼び分けていますが,これらは異なる次数の外積空間の元ですので,言ってみれば,違う世界に住んでいるようなものです.
を基底とするベクトルの形になっていることを,もう一度確認して下さい.(零次微分形式はスカラーに相当.)さて,基底の次数別に何次微分形式などと呼び分けていますが,これらは異なる次数の外積空間の元ですので,言ってみれば,違う世界に住んでいるようなものです.
次数の異なる微分形式の間には,どのような関係があるのでしょうか?(まさか何の関係も無いというわけはなさそうですよね.)
外微分
実は, 外微分 という演算によって,次数の異なる微分形式を関係づけることが出来ます.零次微分形式を一回外微分すると一次微分形式,一次微分形式を一回外微分すると二次微分形式,二次微分形式を一回外微分すると三次微分形式という具合に,外微分を行うことで,微分形式は一つ次数が上の微分形式に対応させられます.
| [*] | この段階では,まだ外微分とは何か,具体的に示していませんので,『そのような関係を与える写像を入れることが出来る』というような言い方に留めておいた方が正確でしょう.しかし,すぐに示すように,外微分も,今までよく知っている微分によく似た計算です. |
いきなりですが,関数の全微分を求める計算を思い出しましょう.ただの関数は零次微分形式ですから, 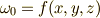 と置きましょう.この 全微分 が次のように書けることは,既に微積分学でお馴染みだと思います.
と置きましょう.この 全微分 が次のように書けることは,既に微積分学でお馴染みだと思います.
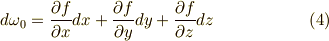
よく見ると,これは一次微分形式の形になっていますね.そこで,関数の全微分を求める計算は,『零次微分形式→一次微分形式』という写像だと考えることも出来るわけです.いまから考える外微分という計算も,関数の全微分を,もっと高次の微分形式にも拡張したものだと考えて下さい.以下の 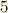 つのルールに基づく演算を 外微分 だと定義します.
つのルールに基づく演算を 外微分 だと定義します.
| [†] | 今までの人生で,全微分を計算したことは何度もあると思いますが,『零次微分形式から一次微分形式への写像』をしていたとは気がつかなかったかもしりません.次からは,全微分を見たら一次微分形式だと思ってみましょう. |
definition
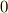 次微分形式
次微分形式 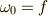 に対し,
に対し, 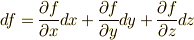 とする.
とする. 次微分形式
次微分形式 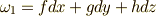 に対し,
に対し, 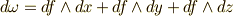 とする.
とする.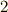 次微分形式
次微分形式 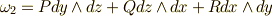 に対して,
に対して, 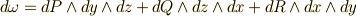 とする.
とする.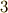 次微分形式
次微分形式 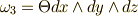 に対して,
に対して,  とする.
とする.- 任意の次数の微分形式について
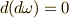 とする.
とする.
五番目の性質は, ポアンカレの補題 として知られるもので,二回連続で外微分を取れば,どんな微分形式でも零になるという主張です.この性質は,また稿を改めて考えます.まず,一次微分形式の外微分を実際に計算してみましょう.(途中で 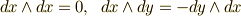 などの性質に注意して下さい.)
などの性質に注意して下さい.)
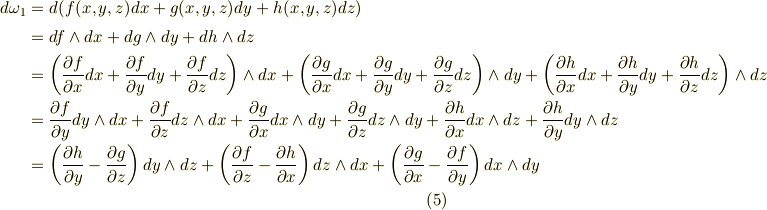
確かに, 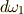 は二次微分形式になっていることが分かります.次に,二次微分形式の外微分も計算してみます.
は二次微分形式になっていることが分かります.次に,二次微分形式の外微分も計算してみます.
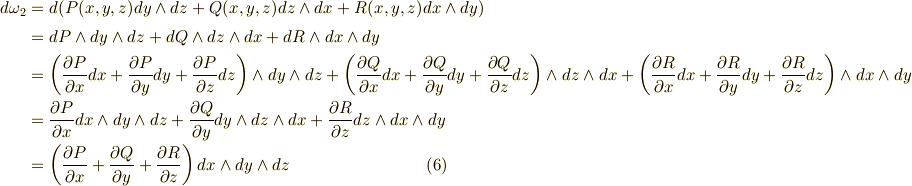
これは三次微分形式になっています.最後の段で,基底の順列と符号にだけ気をつけてください.では,最後に三次微分形式の外微分が 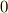 になることを確認してみましょう.
になることを確認してみましょう.
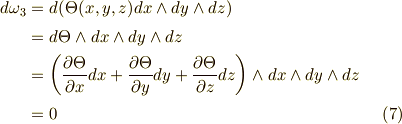
三次微分形式の外微分が 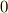 になるのは,
になるのは, 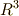 上の微分形式を考えているからです.一般に,
上の微分形式を考えているからです.一般に, 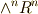 の元の外微分は
の元の外微分は 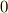 になります.微分形式の外微分を取ると,微分形式の次数が一つ上がるという点を確認して下さい.
になります.微分形式の外微分を取ると,微分形式の次数が一つ上がるという点を確認して下さい.
Important
外微分は微分形式の次数を一つ上げます.(写像 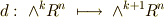 になっています.)
になっています.)
| [‡] | 式 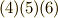 の成分を見て, の成分を見て, 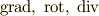 の計算に似ていると思った人はなかなか鋭いです.ベクトル解析に出てきた の計算に似ていると思った人はなかなか鋭いです.ベクトル解析に出てきた 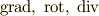 が外微分に対応することは, もう一度grad,div,rot で示します. が外微分に対応することは, もう一度grad,div,rot で示します. |
練習問題
式 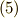 と式
と式 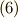 にもう一回外微分を施し,
にもう一回外微分を施し, 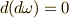 が成り立っていることを確認してみて下さい.
が成り立っていることを確認してみて下さい.
全微分の座標不変性
あまり考えたことがなかったかも知れませんが,全微分は座標系によりません.
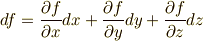
もし,適当な座標変換をして 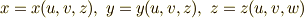 と変数変換できるとすれば,合成関数の微分公式により,次のような式変形が可能です.
と変数変換できるとすれば,合成関数の微分公式により,次のような式変形が可能です.
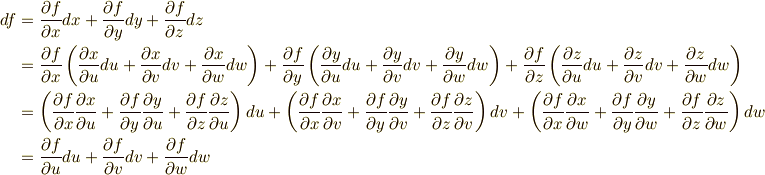
これより 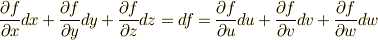 と書くことが出来ます.これはどういうことかと言えば,適当な座標変換
と書くことが出来ます.これはどういうことかと言えば,適当な座標変換 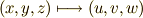 の下で,全微分
の下で,全微分 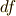 が不変だということです.
が不変だということです.
theorem
全微分は,座標変換に対して不変です.
薄々予想されることですが,全微分の持つこの性質は,全微分を拡張したものである外微分にも引き継がれています.後ほど, 外微分の座標不変性 で詳しく考えてみる予定ですので,その準備として,とりあえず全微分の座標不変性を確認しておいて下さい.
| [§] | もちろん,ここで用いた座標変換とは, 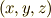 と と 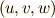 を相互に関係付ける,滑らかな(少なくとも を相互に関係付ける,滑らかな(少なくとも 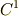 級の)関数による写像を意味しています.あんまり変チクリンな座標変換は考えません.しかし,あとで 微分形式の引き戻し で考えるように,微分形式で考える座標変換は変数の次数が変わる場合(例えば 級の)関数による写像を意味しています.あんまり変チクリンな座標変換は考えません.しかし,あとで 微分形式の引き戻し で考えるように,微分形式で考える座標変換は変数の次数が変わる場合(例えば  )でも,写像が滑らかでさえあれば微分形式を不変に保ちます.通常のテンソル解析では同じ次数の可逆な変換(直交変換など)しか考えなかったことと比べると,微分形式の方がかなり自由度が高そうです. )でも,写像が滑らかでさえあれば微分形式を不変に保ちます.通常のテンソル解析では同じ次数の可逆な変換(直交変換など)しか考えなかったことと比べると,微分形式の方がかなり自由度が高そうです. |