商体
商体とは呼んで名のごとく,分数で作った体です.
ある整域 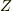 にたいし,
にたいし, 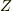 の元
の元 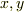 を分母と分子に組み合わせ(ただし分母
を分母と分子に組み合わせ(ただし分母 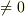 ),
),  の形の集合を作ると,これは体になります.これを 商体 と呼びます. 分数体 , 商の体 などとも呼びます.
の形の集合を作ると,これは体になります.これを 商体 と呼びます. 分数体 , 商の体 などとも呼びます.
例えば,任意の有理数は既約な整数 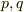 によって
によって  のように分数の形で表現できますので, 有理数体Qは,整数環Zの商体です .
のように分数の形で表現できますので, 有理数体Qは,整数環Zの商体です .
定義は簡単だったと思います.まず,この集合が体になることを,次節で確認してみましょう.
体になること
ポイントは,  の形をした分数が,全て商体は含まれるということです.
の形をした分数が,全て商体は含まれるということです.
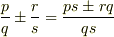 という計算をすると,分母と分子
という計算をすると,分母と分子 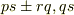 はそれぞれ整域
はそれぞれ整域 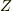 の元ですから,
の元ですから,  も商体に含まれるはずです.
も商体に含まれるはずです.- 同様に,乗法
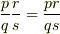 も閉じています.
も閉じています.  に対して
に対して 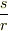 という組み合わせも存在するはずですので,乗法に対し除法があります.
という組み合わせも存在するはずですので,乗法に対し除法があります.
商体を作るもとの集合を整域としたのは,一般の環では零因子を含む場合があるので,期せずして 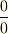 のようなものが出てきてしまって分数同士の積をうまく定義できなくなる可能性を回避するためです.
のようなものが出てきてしまって分数同士の積をうまく定義できなくなる可能性を回避するためです.
より抽象的な定義
もっと難しい議論に備えて,もう少し定義を抽象化しておきます.この節は少々ややこしく,そして長くなりますが,内容的には前節の『分数』を少し抽象化するだけです.この記事の最後の定理や 素体 の記事の定理で,商体の概念を使うので,順番として今ここで紹介しているのですが,商体自体が今後特別に重要なわけでもありません.先を急ぐ人や抽象化の苦手な人は,飛ばして,この次の節に進んでしまっても大丈夫だと思います.
まず,整域 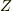 の直積集合
の直積集合 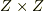 を考えます.
を考えます. 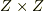 の二つの元,
の二つの元, 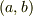 と
と 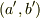 が関係
が関係  を満たすとき,
を満たすとき, 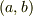 と
と 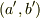 の間に同値関係を定義できます.
の間に同値関係を定義できます.
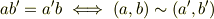
| [*] | この同値関係によって,約分して同じになる 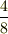 と と 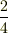 のような分数に対し,その分母・分子の組, のような分数に対し,その分母・分子の組, 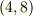 と と  を同値だと見なせるということです.単なる文字の組としては を同値だと見なせるということです.単なる文字の組としては 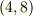 と と  は別のものですが,これらを分子と分母にして分数を作るとなれば,同じものだと考えても良さそうなことが直観的に了解できると思います.きちんと同値関係を示すには,反射律,対称律,推移律が満たされることを確認する必要がありますが( 整数の加法群の剰余類 参照),これは簡単なので自分でやってみて下さい.いきなり抽象的に, は別のものですが,これらを分子と分母にして分数を作るとなれば,同じものだと考えても良さそうなことが直観的に了解できると思います.きちんと同値関係を示すには,反射律,対称律,推移律が満たされることを確認する必要がありますが( 整数の加法群の剰余類 参照),これは簡単なので自分でやってみて下さい.いきなり抽象的に, 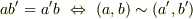 と書かれたら「何のこっちゃ」と感じると思いますが,分数の例に戻って考えれば当然の同値関係だと感じられることでしょう. と書かれたら「何のこっちゃ」と感じると思いますが,分数の例に戻って考えれば当然の同値関係だと感じられることでしょう. |
この同値関係を使って 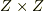 の元を類別できますから,代表元
の元を類別できますから,代表元 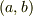 を含む類を
を含む類を ![[a,b]](./2c3d331bc98b44e71cb2aae9edadca7e.png) と表現することにして,
と表現することにして, 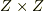 の商集合
の商集合 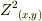 を考えます.つまり,
を考えます.つまり, ![[a,b]](./2c3d331bc98b44e71cb2aae9edadca7e.png) のような類を個々の元とする集合を考えるということです.さて,ここで別に集合
のような類を個々の元とする集合を考えるということです.さて,ここで別に集合 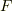 を考え,
を考え, 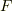 の元
の元 ![X_{[a,b]}](./ac4d2503d64834b4d6eb916a60df0bd9.png) と
と 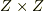 の類
の類 ![[a,b]](./2c3d331bc98b44e71cb2aae9edadca7e.png) を,写像
を,写像 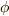 によって対応させてみましょう.
によって対応させてみましょう.
![\phi : \ [a,b] \in {Z^{2}}_{(x,y)} \ \ \longmapsto \ \ X_{([a,b])} \in F](./0b6d87d44cd54dce01f62fb840e83264.png)
この写像は一対一の単射だとします.また, 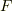 の元には,次のように二つの演算『加法』と『乗法』を定義できるとします.添字に注意してください.
の元には,次のように二つの演算『加法』と『乗法』を定義できるとします.添字に注意してください.
![X_{[a,b]}+X_{[c,d]}=X_{[ad+bc,bd]} \tag{1}](./02f5a4a99bd12e314801b2182677e5a7.png)
![X_{[a,b]}X_{[c,d]}=X_{[ac,bd]} \tag{2}](./093d3bed3df42d24183c7a5581376b75.png)
加法の零元は ![X_{[0,1]}](./987ca914465f09f51d0ca98fbeab2cfd.png) ,乗法の単位元は
,乗法の単位元は ![X_{[1,1]}](./16a77827e2e281b7f5afc19e32bf1ec4.png) です.また加法の逆元は
です.また加法の逆元は ![-X_{[a,b]}=X_{[-a,b]}](./cb21a2c96da3102c9e40477630574e55.png) ,乗法の逆元は
,乗法の逆元は ![{X_{[a,b]}}^{-1}=X_{[b,a]}](./57a68bd0c3fa515920e86ec194d30dc1.png) と置くと,うまく四則演算を定義できます.
と置くと,うまく四則演算を定義できます. 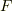 は式
は式 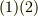 で定義される加法と乗法によって体になります.(この加法と乗法が,結合則,交換則,分配則を満たすことの証明は省略します.)
で定義される加法と乗法によって体になります.(この加法と乗法が,結合則,交換則,分配則を満たすことの証明は省略します.)
| [†] | 式 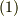 と式 と式  を最初に見せられて,これが加法と乗法だと言われたら,見慣れない算法なので吃驚してしまうと思います.しかし, を最初に見せられて,これが加法と乗法だと言われたら,見慣れない算法なので吃驚してしまうと思います.しかし, ![X_{[a,b]}](./ac4d2503d64834b4d6eb916a60df0bd9.png) を を  に対応させ,式 に対応させ,式 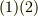 を分数の足し算や掛け算だと見れば納得が行くことでしょう.純粋に抽象的な立場から,いきなり式 を分数の足し算や掛け算だと見れば納得が行くことでしょう.純粋に抽象的な立場から,いきなり式 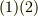 によって加法と乗法を定義すれば体ができる,と説明する方がエレガントかも知れませんが,やはり慣れるまでは分数に戻りながら理解していく方が良いと思います. によって加法と乗法を定義すれば体ができる,と説明する方がエレガントかも知れませんが,やはり慣れるまでは分数に戻りながら理解していく方が良いと思います. |
次に,整域 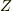 から体
から体 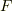 への写像を次のように定めてみます.
への写像を次のように定めてみます.
![\psi : \psi (a) = X_{[a,e]} \ \ (a \in Z, \ \phi (a) \in F)](./a85d51381acb060ffdc089608d37dc9d.png)
この写像は一対一に像が決まりますから単射で,しかも加法と乗法に関して次の二式を満たすため,準同型写像になっています.
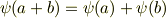
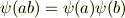
いま,整域  に対応する
に対応する  の元として,
の元として, ![[a,e]](./a0a8a16c7afe64d74300f218749c42ea.png) のように,括弧の右側が単位元
のように,括弧の右側が単位元  のものだけを考えましたが,一般に
のものだけを考えましたが,一般に 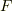 の元
の元 ![[a,b]](./2c3d331bc98b44e71cb2aae9edadca7e.png) は
は ![[a,b]=[a,e][e,b]=\psi (a){\psi }^{-1}(b)](./0b822aaf731249d5d1c6cc835b7ad5d1.png) の形をしてますので,
の形をしてますので, 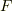 は,写像
は,写像 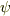 による
による 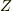 の商体になっていると言えます.
の商体になっていると言えます.
ここまでの議論を踏まえ,次の二つの条件を満たす集合を商体と呼ぶことにします.(繰り返しになりますが,これは前節で見た分数の体を,抽象的に拡張しているだけです.)
- 整域
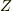 と体
と体 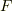 に対し,ある単射の準同型写像
に対し,ある単射の準同型写像 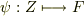 が存在します.
が存在します. - 一般に
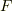 の元は,整域の元
の元は,整域の元 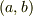 と写像
と写像 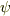 を使って,
を使って, 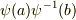 の形で表現されます.
の形で表現されます.
大事な定理
体の拡大に関連して,商体の概念が出てくる定理を一つ紹介しておきます.
theorem
整域 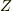 を含む体の中で最小のものは,
を含む体の中で最小のものは, 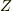 の商体です.
の商体です.
proof
整域 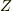 を含む体を
を含む体を 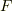 とします.
とします. 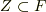 .
. 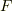 の部分集合
の部分集合 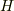 を,
を, 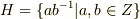 と置くと,
と置くと, 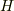 は体の条件を満たし,部分体になります( 部分体 参照).特に
は体の条件を満たし,部分体になります( 部分体 参照).特に  と置くと,
と置くと, 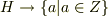 となり,
となり, 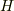 は
は 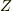 を含むことが分かります.
を含むことが分かります. 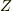 から
から 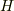 の元への単射な準同型写像
の元への単射な準同型写像 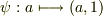 を定めると,
を定めると, 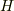 は商体の条件
は商体の条件 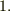 〜
〜 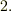 を満たし,商体となります.
を満たし,商体となります. 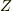 の商体は,
の商体は, 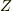 を含む任意の体に対してその部分集合となるのですから,
を含む任意の体に対してその部分集合となるのですから, 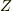 の商体が
の商体が 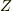 を含む最小の体だと言えます.■
を含む最小の体だと言えます.■
単に分数を集めただけに見えた商体ですが,この定理は体の拡大系列を考えるときに役に立ちそうですね.例えばこの定理より,整数環を含む最小の体は,有理数体だということが分かります.
theorem
整数環を含む最小の体は,有理数体です.
次の定理は, 素体 の記事で定理の証明に使いますので,ここで証明しておきます.
theorem
整域 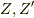 が同型ならば,商体
が同型ならば,商体 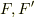 も同型になります.
も同型になります.
proof
同型写像  に対し,
に対し, 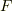 から
から 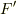 への写像
への写像 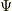 を
を 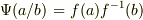 と定めれば
と定めれば 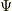 も同型写像になります.■
も同型写像になります.■