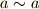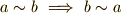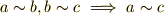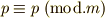整数の加法群の剰余類
整数全体は,加法に関して群をつくるということでした( 群の公理 の例6を参照).これを整数の加法群と呼びます.このページでは,ある整数で割ったときの余りに応じて,整数全体をグループ分けすること(類別です)を勉強します.
類別の概念自体は, 類別 で勉強しましたが,この記事では同値関係と併せて,さらに理解を深めることを目標とします.
合同式
整数論を習っていない人のために,ここで少し合同式の復習をしておきます.
ある整数 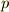 を,整数
を,整数 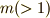 で割ると,ただ一通りに次のように表現することができます.
で割ると,ただ一通りに次のように表現することができます. 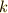 も整数です.
も整数です.
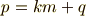
ここで, 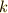 を 整商 ,
を 整商 ,  を 剰余 と呼びます.剰余とは,要するに余りです.
を 剰余 と呼びます.剰余とは,要するに余りです. 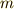 で割ったとき,幾つ余るかという点だけに着目すると
で割ったとき,幾つ余るかという点だけに着目すると 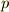 と
と  は同じですから,これを次のように書き,『法
は同じですから,これを次のように書き,『法 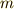 について合同である』と言います.『
について合同である』と言います.『 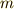 で割ったときの余りが等しいよ』という意味です.これを合同式と言います.
で割ったときの余りが等しいよ』という意味です.これを合同式と言います. 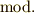 とあるのが,何の数で割ったかを示す記号です.
とあるのが,何の数で割ったかを示す記号です.
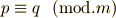
| [*] | ここに出てくる記号 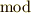 は は 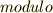 の略です.そのままモドと読む人もいますが,正しくはモジュロです.例えば の略です.そのままモドと読む人もいますが,正しくはモジュロです.例えば 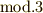 を『 を『 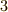 を法として』と読んでもいいし『モジュロ3』と読んでも良いです.ラテン語で基準,単位などを意味する を法として』と読んでもいいし『モジュロ3』と読んでも良いです.ラテン語で基準,単位などを意味する 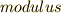 から派生した前置詞が から派生した前置詞が 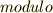 です. です. |
同値関係
さて,群の類別のページで同値関係という概念を勉強しましたが,二つの整数 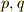 は,実は合同式によって同値関係で結ばれると言えるのです.同値関係は,集合の二つの元
は,実は合同式によって同値関係で結ばれると言えるのです.同値関係は,集合の二つの元 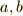 について,次の三つの関係が成り立つような関係と定義されます.
について,次の三つの関係が成り立つような関係と定義されます.
最初の条件は,同値関係 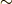 がなりたつとき,どんな元も自分自身とは同値だという主張( 反射律 ),二番目の条件は,同値関係はどちらの視点から見ても成り立つという主張( 対称律 )です.三番目の条件は, 推移律 と呼ばれます.
がなりたつとき,どんな元も自分自身とは同値だという主張( 反射律 ),二番目の条件は,同値関係はどちらの視点から見ても成り立つという主張( 対称律 )です.三番目の条件は, 推移律 と呼ばれます.
剰余類
さて,二つの整数の間になりたつ合同関係は,同値関係の3つの条件を満たします.
そこで,整数全体は,合同関係を使って類別できるといえます.一般に,集合は,元に同値関係がなりたつとき,類別できるのでした( 類別 を参照).例えば, 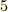 を法とした合同関係を考えましょう.すると,どのような整数も,
を法とした合同関係を考えましょう.すると,どのような整数も, 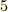 で割ったときの余りは
で割ったときの余りは 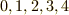 のどれかであるはずですので,整数全体を5つに類別できることになります.
のどれかであるはずですので,整数全体を5つに類別できることになります.
余りが 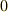 の類:
の類: 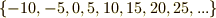
余りが 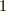 の類:
の類: 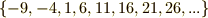
余りが 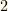 の類:
の類: 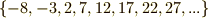
余りが 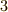 の類:
の類: 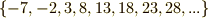
余りが 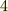 の類:
の類: 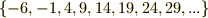
各類には,他の類と重複するような元がないことを確認してください.( 剰余類 につづく.)
| [†] | 余力のある人は 剰余類 に進む前に,余りが 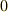 の類だけは部分群になっていることを確認してみて下さい. の類だけは部分群になっていることを確認してみて下さい. |