テンソルの主軸1
この記事の内容は,応用上,物理や工学で重要だと思います..主に二階のテンソルだけに関係する話で,知識として必要なのは,今までのベクトルやテンソルの内容だけですが,行列の計算に慣れていると心強いです
固有値問題
一般に,二階のテンソル 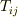 をベクトル
をベクトル 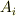 に作用させると,何か座標変換されて違うベクトル
に作用させると,何か座標変換されて違うベクトル 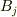 になってしまいます.いま,座標系として正規直交座標系を仮定し,添字は全て右下に揃えることにします.
になってしまいます.いま,座標系として正規直交座標系を仮定し,添字は全て右下に揃えることにします.

| [*] | 一般のアフィン座標を取っても同様の議論は展開できるのですが,あまりにも計算と表記が煩雑になるので,直交座標系としました.工学的な応用を考えている人は,ほとんど正規直交基底以外使わないと思いますので,この記事に関しては一般化する必要をあまり感じなかったということもあります.直交座標系では共変基底と反変基底が同一になり,添字の上下の区別もしなくて良くなります.一般のアフィン座標の場合にどのように計算したら良いのかは後で少し方針だけ触れます. |
ここで 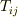 を関数だと見て,
を関数だと見て, 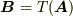 のように考えてみましょう.つまり,何かベクトル
のように考えてみましょう.つまり,何かベクトル 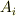 を放り込むと,違うベクトル
を放り込むと,違うベクトル 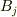 が返って来るブラックボックスだと見るわけです.どんな
が返って来るブラックボックスだと見るわけです.どんな 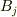 が出てくるかは,もちろん
が出てくるかは,もちろん 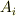 によります.
によります.
色々な 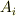 を試してみると,中にはスカラー
を試してみると,中にはスカラー 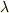 を使って
を使って  と書けるものがあるかも知れません.このような
と書けるものがあるかも知れません.このような 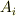 が存在するなら,
が存在するなら, 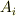 を
を 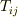 の 固有ベクトル と呼び,
の 固有ベクトル と呼び, 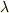 を 固有値 と呼びます.
を 固有値 と呼びます.

式 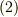 を行列表記するとと,次のようになります.
を行列表記するとと,次のようになります.

式 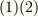 の意味をもう少し図形的に考えてみましょう.座標変換というのは,あくまでも座標系の取り方,つまり観測者の視点を変えることです.一般に,眺める向きを変えれば,ベクトルの向きや長さも違ってみえます.(それが式
の意味をもう少し図形的に考えてみましょう.座標変換というのは,あくまでも座標系の取り方,つまり観測者の視点を変えることです.一般に,眺める向きを変えれば,ベクトルの向きや長さも違ってみえます.(それが式 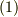 の意味するところです.)ところが,座標系をある特定の向きに取ると,つまり式
の意味するところです.)ところが,座標系をある特定の向きに取ると,つまり式 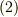 を満たす
を満たす 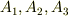 の基底の取り方に最初から立って見てみると,
の基底の取り方に最初から立って見てみると, 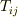 によって座標変換した後も,ベクトルの向きは変わらず,長さだけが
によって座標変換した後も,ベクトルの向きは変わらず,長さだけが 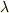 倍されたように見えるということです.この特定の向きを,
倍されたように見えるということです.この特定の向きを, 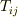 の 主方向 と呼び,主方向を向いた座標軸を 主軸 と呼びます.
の 主方向 と呼び,主方向を向いた座標軸を 主軸 と呼びます.
線形代数を勉強した読者の方なら分かると思いますが,二階のテンソルの主方向と固有値を定める問題は,行列の固有値・固有ベクトルを求める問題と同じです.
固有値・固有ベクトル・主方向を求めてみる
実際に固有値・固有ベクトル・主方向を求めてみましょう.式 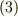 の右辺を移項して次式がなりたちます.この後の計算は,普通の線形代数の教科書に出ているものです.
の右辺を移項して次式がなりたちます.この後の計算は,普通の線形代数の教科書に出ているものです.
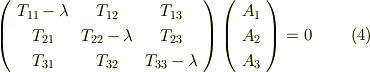
いま 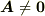 を仮定していますので,式
を仮定していますので,式  がなりたつためには行列
がなりたつためには行列 ![[T_{ij}-\lambda \delta_{ij}]](./8e732dfb87323c72905af9ff080c6524.png) の行列式が零にならなければなりません.
の行列式が零にならなければなりません.
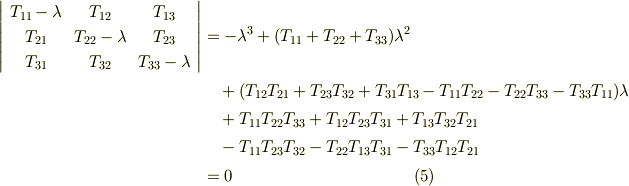
式 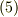 はテンソル
はテンソル 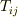 の 固有方程式 もしくは 特性方程式 と呼ばれます.
の 固有方程式 もしくは 特性方程式 と呼ばれます.
固有方程式が重解を持たない場合の固有ベクトル
固有方程式は三次方程式ですので,重解を持たない場合,三つの固有値 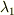 ,
, 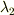 ,
, 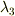 が解として出てきます.また,個々の固有値に対応して,式
が解として出てきます.また,個々の固有値に対応して,式 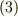 より,固有ベクトルが決まります.固有値
より,固有ベクトルが決まります.固有値 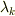 に対応する固有ベクトルを
に対応する固有ベクトルを 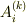 と表記することにします.
と表記することにします. 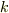 は固有値の番号
は固有値の番号 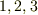 を表わすもので,テンソルの添字や冪乗の意味ではありません.
を表わすもので,テンソルの添字や冪乗の意味ではありません.
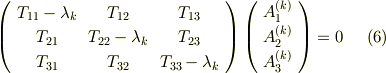
式 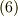 より,クラメルの公式を使って
より,クラメルの公式を使って 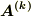 の係数は次の関係式を満たすことが導けます.(クラメルの公式は線形代数の本で調べてください.)
の係数は次の関係式を満たすことが導けます.(クラメルの公式は線形代数の本で調べてください.)
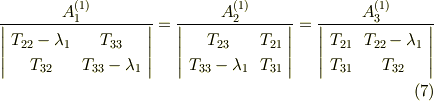
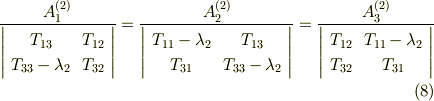
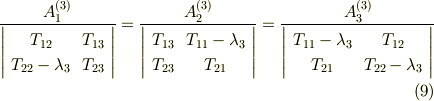
これらは固有値  に対して,固有ベクトルの成分
に対して,固有ベクトルの成分 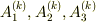 が満たす空間直線の方程式ですが,決まるのは直線の向きだけで,大きさ
が満たす空間直線の方程式ですが,決まるのは直線の向きだけで,大きさ 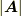 までは決まらないことに注意してください. 式
までは決まらないことに注意してください. 式 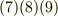 より,固有ベクトルの方向ベクトルを次のように書けることがわかります.これがテンソルの主方向になります.
より,固有ベクトルの方向ベクトルを次のように書けることがわかります.これがテンソルの主方向になります.
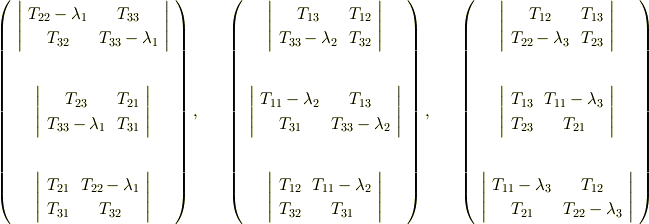
一般のアフィン座標系の場合
一般のアフィン座標系の場合,テンソルと固有値,固有ベクトルの関係は式 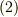 の代わりに次式になります.
の代わりに次式になります.

右辺の 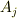 を
を 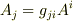 と置いて反変成分に揃えると,次式になります.
と置いて反変成分に揃えると,次式になります.

ここから 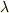 を決めるために
を決めるために 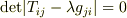 を固有方程式として解いても良いのですが,計量テンソル
を固有方程式として解いても良いのですが,計量テンソル  が面倒です.式
が面倒です.式 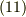 で,共変テンソルではなく,混合テンソルを使うように式変形すれば,計量テンソルの性質
で,共変テンソルではなく,混合テンソルを使うように式変形すれば,計量テンソルの性質 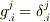 より,形式的に計量テンソルを消去して式
より,形式的に計量テンソルを消去して式 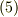 と同じ形に帰着させることができます.式
と同じ形に帰着させることができます.式 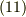 の両辺に
の両辺に 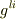 を掛けます.
を掛けます.
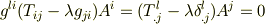
ここから得られる固有方程式は,形式的に式 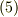 と同じですので,後はいままでと同じ議論が適用できます.
と同じですので,後はいままでと同じ議論が適用できます.
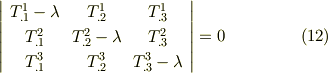
( テンソルの主軸2 に続きます.)