曲率と曲率半径
曲線が曲がっているとき,その局所的な曲がり具合を円に近似することができます.その円の半径を 曲率半径 , 曲率半径の逆数を 曲率 と言います.すでに フレネ=セレの式 で,曲率は  として登場していますが,この記事ではまず,曲率を高校数学の範囲でも分かるように古典的に導いてみたいと思います.
として登場していますが,この記事ではまず,曲率を高校数学の範囲でも分かるように古典的に導いてみたいと思います.
読者の多くの方が,微積分の勉強で,曲線の微小部分を接線で近似する,という見方に触れたことがあると思います.曲線を直線で近似とはずいぶん乱暴な話ですが,これは一番簡単な近似で,一次近似とも言うべきものです.
もう少し曲がり具合を表現しようと頑張ってみたのが,曲がり具合を円弧で近似する二次近似です.それでも,一般の複雑な曲線の曲がり具合を表現するには簡単すぎますが,直線よりかは大分ましでしょう.曲率を,曲線の曲がり具合の二次近似だと考えると少し見通しが良くなると思います.最初のセクションではベクトルを使いません.図を見て意味を考えながら,曲率の式の導出を味わって下さい.できれば,実際に自分で計算してみて下さい.
曲率と曲率半径
まず,曲線の微小部分 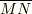 の長さを
の長さを 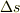 と置き,
と置き, 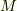 点における接線の傾きと,
点における接線の傾きと, 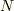 点における接線の傾きの差を
点における接線の傾きの差を 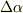 とします.
とします.
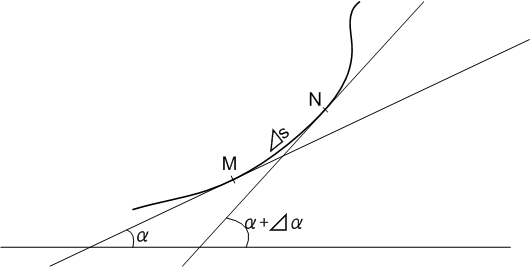
図1:曲線の微小部分.
もしも, 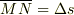 が円弧だとすれば,円の中心を
が円弧だとすれば,円の中心を 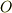 ,
, 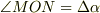 ,円の半径を
,円の半径を 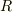 として,
として, 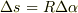 がなりたつはずです(次図).円弧の長さ,中心角が分かっていて,半径を求めたいのなら次のような形にしておけば良いでしょう. (中心角が
がなりたつはずです(次図).円弧の長さ,中心角が分かっていて,半径を求めたいのなら次のような形にしておけば良いでしょう. (中心角が 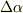 になることは,ちょっと考えれば分かります.)
になることは,ちょっと考えれば分かります.)


図2:円弧の場合.
図 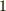 の曲線の微小部分は,本当は円弧ではありませんが,十分に微小な長さを取れば円弧に近似できると考え,このときの半径を 曲率半径 と呼んで
の曲線の微小部分は,本当は円弧ではありませんが,十分に微小な長さを取れば円弧に近似できると考え,このときの半径を 曲率半径 と呼んで 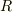 と書きます.
と書きます.

式 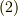 は,先ほどの円弧における,弧長,中心角,半径の関係式
は,先ほどの円弧における,弧長,中心角,半径の関係式 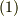 を曲線の微小長さに適用しただけのものですが,これを曲率半径の定義とします.『十分に小さなカーブは,円弧に近似できる』という考えが基になっています.
を曲線の微小長さに適用しただけのものですが,これを曲率半径の定義とします.『十分に小さなカーブは,円弧に近似できる』という考えが基になっています.
曲率半径
関数 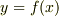 の形で表わされる曲線の曲率半径と曲率を求めてみます.まず,式
の形で表わされる曲線の曲率半径と曲率を求めてみます.まず,式 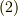 の分子にある
の分子にある 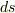 は,ピタゴラスの定理を使って次のように表わせるでしょう.
は,ピタゴラスの定理を使って次のように表わせるでしょう.
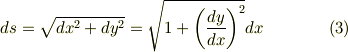
次に分母の 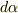 を求めてみましょう.図
を求めてみましょう.図  の点
の点 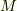 における曲線の傾きは,微分係数の定義より
における曲線の傾きは,微分係数の定義より 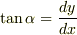 と与えられます.
と与えられます. 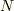 点における傾きは,
点における傾きは, 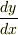 の変化分も考えて
の変化分も考えて 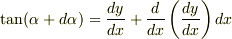 で与えられるでしょう.
で与えられるでしょう. 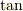 の加法定理を使って
の加法定理を使って  を次のように式変形します.
を次のように式変形します.
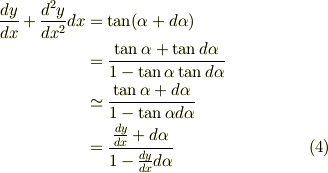
途中, 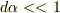 より
より  と見なせることを使いました.式
と見なせることを使いました.式 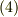 の両辺を
の両辺を 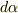 についてまとめると次式を得ます.(
についてまとめると次式を得ます.( 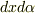 の項は二次の微小量なので落とします.)
の項は二次の微小量なので落とします.)
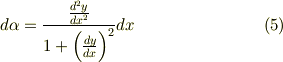
式 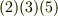 より次式を得ます.
より次式を得ます.

式 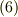 が,曲線が陽関数
が,曲線が陽関数 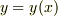 で表わされる場合に,曲率を与える公式となります.曲線が陰関数
で表わされる場合に,曲率を与える公式となります.曲線が陰関数 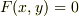 で与えられる場合,パラメータ表示
で与えられる場合,パラメータ表示 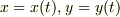 で与えられる場合,極座標
で与えられる場合,極座標 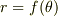 で与えられる場合の公式を以下に示します.式
で与えられる場合の公式を以下に示します.式 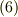 の導出を参考に,これらの公式は練習問題だと思って自分で導いてみて下さい.
の導出を参考に,これらの公式は練習問題だと思って自分で導いてみて下さい.
【陰関数表示の場合】
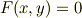
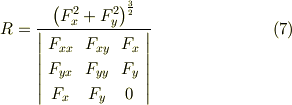
ただし,添字の  や
や 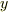 は
は 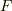 の偏微分を表わしているものとします.
の偏微分を表わしているものとします.
【パラメーター表示の場合】
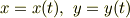
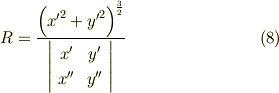
ダッシュは, 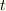 による微分を表わすものとします.
による微分を表わすものとします.
【極座標表示の場合】
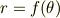

円の方程式, 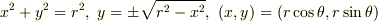 などを代入し,曲率半径が
などを代入し,曲率半径が  になることを確認してみて下さい.
になることを確認してみて下さい.
曲率
曲率  は曲率半径の逆数として定義されます.
は曲率半径の逆数として定義されます.

また,フレネ=セレの式に出てきた  は
は  として定義されましたが,このままでは円とか半径とかいう図形的な様子が分かりにくいと思います.
として定義されましたが,このままでは円とか半径とかいう図形的な様子が分かりにくいと思います.  が確かに曲率を表わしていることは次のようにして確認できます.曲線を
が確かに曲率を表わしていることは次のようにして確認できます.曲線を  ,接線ベクトルを
,接線ベクトルを  ,主法線ベクトルを
,主法線ベクトルを 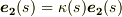 とします.やや天下り的ですが,いきなり点
とします.やや天下り的ですが,いきなり点 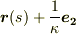 を微分します.
を微分します.
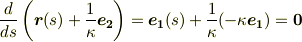
この式は,点 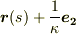 が定点で,
が定点で, 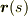 は点
は点 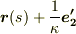 を中心とする半径
を中心とする半径 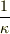 の円を表わしていると読むことが出来ます.曲率半径が
の円を表わしていると読むことが出来ます.曲率半径が 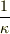 なので,曲率は定義より
なので,曲率は定義より  です.確かに,フレネ=セレの式に出てきた
です.確かに,フレネ=セレの式に出てきた  も,先ほど定義した曲率と同じものだということが確認できました.
も,先ほど定義した曲率と同じものだということが確認できました.
接ベクトル
すでに フレネ=セレの式 で勉強したように,曲率は,曲線の接ベクトルを弧長パラメーターで微分したベクトルの絶対値として与えられます.

主法線を使えば,次の関係式が言えます.
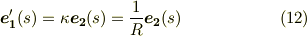
もしくは,フレネ=セレの式の最初の二行二列を取って,次の関係式が言えます.これは平面曲線における,接線ベクトル,法線ベクトル,曲率の関係式になります.
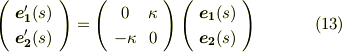
曲率とは呼んで名の如く,曲線の曲がり具合を表わすパラメーターですが,曲率が  の場合,すなわち曲線がまっすぐな場合,式
の場合,すなわち曲線がまっすぐな場合,式 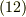 より
より  となり,積分して
となり,積分して 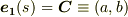 (
( 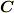 は何か定ベクトル)を得ます.曲線の方程式を
は何か定ベクトル)を得ます.曲線の方程式を 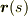 とすれば,定義より
とすれば,定義より 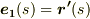 ですので,
ですので, 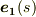 をもう一度積分して
をもう一度積分して 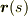 の表式は次式のようになります.
の表式は次式のようになります.
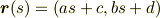
これは  をパラメーターとする直線の方程式ですね.(ただし
をパラメーターとする直線の方程式ですね.(ただし  は積分定数とします.)当たり前のことのようですが, 曲率が零なのは直線である ことが分かりました.
は積分定数とします.)当たり前のことのようですが, 曲率が零なのは直線である ことが分かりました.
曲線の方程式 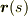 を次のように級数展開すると,曲率の意味はさらに明快です.
を次のように級数展開すると,曲率の意味はさらに明快です.
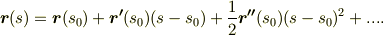
ここに, 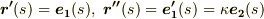 を代入します.
を代入します.
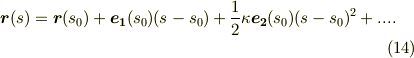
曲率は式 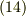 で三次以上の項を切り捨てた場合の,二次の項に出て来る係数になっています.(二次以降の項を切り捨てると,式
で三次以上の項を切り捨てた場合の,二次の項に出て来る係数になっています.(二次以降の項を切り捨てると,式 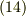 は,
は, 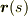 を点
を点  における接線で曲線を近似する式となります.)
における接線で曲線を近似する式となります.)
練習問題
当然のことですが,半径 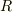 の円の曲率半径が
の円の曲率半径が 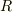 ,曲率が
,曲率が 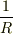 になることを練習問題として確認してみましょう.接ベクトルや主法線ベクトルを使う練習です.円の半径を
になることを練習問題として確認してみましょう.接ベクトルや主法線ベクトルを使う練習です.円の半径を  ,中心角を
,中心角を 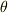 として,円の方程式をパラメーター
として,円の方程式をパラメーター 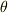 で表示します.
で表示します.
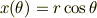

変位  と
と 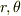 の間には
の間には 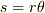 の関係がありますから,ここでも
の関係がありますから,ここでも  を標準パラメーター
を標準パラメーター  を用いた表現に置き換えます.
を用いた表現に置き換えます.


定義より,接線ベクトル 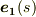 は式
は式 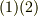 を用いて次のように決まります.
を用いて次のように決まります.
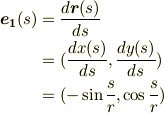
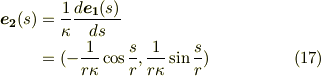
式 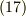 で
で 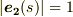 とおけば,
とおけば, 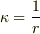 が求まります.
が求まります.