フレネ=セレの公式
フレネの標構  は互いに直交するように選びましたので,互いに次の関係が成り立っています.
は互いに直交するように選びましたので,互いに次の関係が成り立っています.



当然の式のように思いますが,式 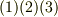 を微分することで,少し面白い公式を導くことが出来ます.
を微分することで,少し面白い公式を導くことが出来ます. 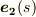 の定義式も思い出しておいて下さい.
の定義式も思い出しておいて下さい.

フレネ=セレの公式
まず式 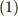 の両辺を微分します.
の両辺を微分します.
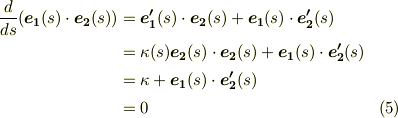
ここで右辺に出てきた 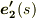 をどう表わすかが問題ですが,
をどう表わすかが問題ですが, 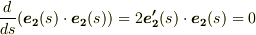 より,
より, 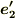 は
は 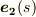 に直交する向きのベクトルですから,
に直交する向きのベクトルですから,  と
と 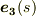 の張る平面に乗るはずで,適当な定数
の張る平面に乗るはずで,適当な定数  を用いて,次式のように
を用いて,次式のように  と
と 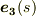 の一次結合で表わせるはずです.
の一次結合で表わせるはずです.
さらに式 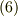 の両辺と
の両辺と  の内積を取ると,
の内積を取ると, 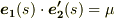 となりますが,これを式
となりますが,これを式 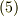 に代入すれば,
に代入すれば, 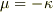 が決定します.
が決定します.
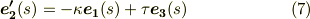
また,式 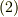 を微分することで次式を得ます.
を微分することで次式を得ます.
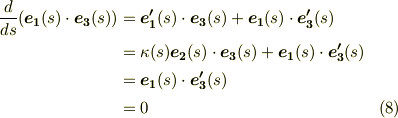
右辺に出てきた 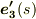 は,式
は,式 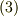 を微分することで,もう少し変形できます.何をやっているか,だんだんこんがらがって来たと思いますが,もう少しだけ頑張ってついて来て下さい.
を微分することで,もう少し変形できます.何をやっているか,だんだんこんがらがって来たと思いますが,もう少しだけ頑張ってついて来て下さい.

先ほどと同様, 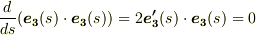 より,
より, 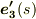 は
は 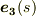 に直交しますが,式
に直交しますが,式 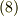 より
より  にも直交すると言えるため,結局
にも直交すると言えるため,結局 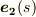 に平行なベクトルだと分かります.そこで
に平行なベクトルだと分かります.そこで 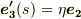 と置いて式
と置いて式 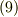 に代入すると,
に代入すると, 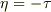 が決まります.
が決まります.

式  をまとめると,次のような綺麗な公式を得ることができます.これを フレネ=セレの公式 と呼びます.これを求めたくて,今までごちゃごちゃ計算していたのでした.
をまとめると,次のような綺麗な公式を得ることができます.これを フレネ=セレの公式 と呼びます.これを求めたくて,今までごちゃごちゃ計算していたのでした.
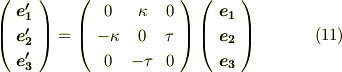
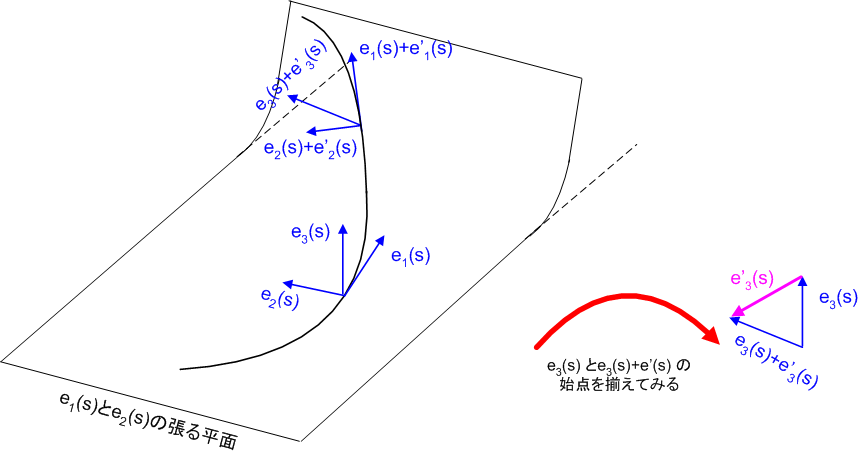
ここに出てきた  の物理的な意味を考えてみましょう.
の物理的な意味を考えてみましょう. 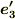 が
が 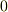 でないということは,次図のように局所的に平面曲線とみなせる曲線が,この平面の法線方向に変化していくということです.イメージとしては,図中の上下方向への曲線の変化率を表わすのが
でないということは,次図のように局所的に平面曲線とみなせる曲線が,この平面の法線方向に変化していくということです.イメージとしては,図中の上下方向への曲線の変化率を表わすのが  だと言えそうです.
だと言えそうです.  のことを 捩率 とよびます.平面曲線では,常に
のことを 捩率 とよびます.平面曲線では,常に 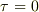 となります.
となります.
| [*] | フレネ=セレの公式に出てきた行列が,美しい形をしていることに気がついたと思います.これは歪対称行列と呼ばれる形で,転置行列がもとの行列の符号を逆にしたものになっています.実は,これは当然の結果で,直交変換の一次近似は歪対称行列で表わされるのでした.これについては 無限小回転 を参照して下さい. |
フレネとセレについて
フレネ=セレの公式にその名を留めるフレネとセレですが,どのような数学者だったのでしょうか?フレネ  は,フランス南部の町ペリグーのカツラ職人の家に生まれました.
は,フランス南部の町ペリグーのカツラ職人の家に生まれました. 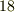 世紀までは大きな需要のあったカツラも,フランス革命後は旧体制の象徴として次第に使われなくなったため,家計は苦しかったようです.曲線に沿って一緒に動く動構を取るというアイデアを思いつき,フレネ=セレの公式を導きましたが,フレネが示したのは
世紀までは大きな需要のあったカツラも,フランス革命後は旧体制の象徴として次第に使われなくなったため,家計は苦しかったようです.曲線に沿って一緒に動く動構を取るというアイデアを思いつき,フレネ=セレの公式を導きましたが,フレネが示したのは 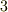 本のうち
本のうち 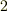 本だけのようです.セレ(
本だけのようです.セレ(  )もパリ生まれのフランス人で,後にはソルボンヌ大学で解析学の教授をしていた人です.微分幾何の分野に色々な貢献がありますが,フレネ=セレの公式もフレネとは全く独立に導きました.ちゃんと
)もパリ生まれのフランス人で,後にはソルボンヌ大学で解析学の教授をしていた人です.微分幾何の分野に色々な貢献がありますが,フレネ=セレの公式もフレネとは全く独立に導きました.ちゃんと 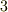 本とも求めたので,セレの方に敬意を表してセレ=フレネの公式と呼ぶ人もいるようです.
本とも求めたので,セレの方に敬意を表してセレ=フレネの公式と呼ぶ人もいるようです.