高校数学で空気抵抗ありの落下運動
日本の高校で行われている物理の授業では,物体の落下については空気抵抗を無視する場合だけ扱っています. 発展的な話題として空気抵抗が取り上げられたとしても,落下し始めてからたくさん時間が経った後の速度を求めるくらいしかやりません. [*]
だけど空気抵抗があるときの落下運動というのは,Newtonも著書「プリンキピア」に書いたくらい歴史ある問題です.
そして高校で習う数学の知識だけでも,速さに比例する空気抵抗の問題を解くことは可能なのです. せっかくならば,たくさん時間が経過した後の速度を求めるだけでなく,時間とともに速度がどんな具合に増えていくのかってことも求めてみましょう.
ちなみに,同じ問題を大学では 微分方程式を使って解きます . 本質的にやっていることは一緒なのですが,微分方程式を使う方が機械的にできて,楽かもしれません. ここでは,高校で習う数学の知識だけで求める…というお遊びです. [†]
| [*] | 空気抵抗を考えているときに落下し始めてから“たくさん時間が経った後の速度”のことを「終端速度」と呼んだりします.これを求めることしかしないってのは,文科省の学習指導要領解説に“空気抵抗については定性的な話題に留めること”と記載されている影響が強いのでしょう. |
| [†] | なお高校で習う数学の知識といっているのは,「等比数列」の知識と「極限」の操作です.それらに関する解説は,他をご参照ください. |
状況設定
落下している物体に働く空気抵抗は,いろいろなパターンを考えることができます. だけど,解析しやすいものといえば,速さの1乗に比例する空気抵抗です.そして速さに比例する空気抵抗は,物体の速さが遅いときには,実験結果とよく一致することが知られています.
そこで,ここでも速さの1乗に比例する空気抵抗を考えたいと思います.
比例定数を  と書くことにしましょう.空気抵抗の大きさ
と書くことにしましょう.空気抵抗の大きさ 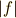 は,
は,
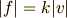
ということになります.  と書いたのは物体の速度です.
と書いたのは物体の速度です.
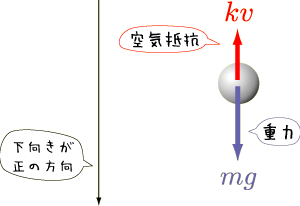
位置も速度も力の向きも,すべて下方向を正の方向だと決めましょう.反対に上方向を正だと決めてもいいのですが,これは単に趣味の問題. このページ内では,下向きを正とします.
たくさん時間が経った後の速度(終端速度)
落下し始めたときは,空気抵抗の大きさと重力の大きさは違うはずで,物体は加速か減速をすることになるでしょう. だけど,たくさん時間が経った後には,空気抵抗と重力がちょうどつり合う状態になるはずです.それを式で表すと,たくさん時間が経った後では,

ということ. 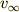 というのは,“たくさん(=
というのは,“たくさん(= 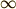 )時間が経った”という意味を込めて,
)時間が経った”という意味を込めて,  に小さく
に小さく 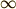 を付けて書きました.
を付けて書きました.
この式で  を左辺に移項して,両辺を
を左辺に移項して,両辺を 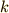 で割り算すれば,たくさん時間が経った後の速度がわかります.
で割り算すれば,たくさん時間が経った後の速度がわかります.

ですね. 物体はこの速度に達したら,それ以上は加速も減速もせず,等速で落下を続けることになるでしょう. (これが,雨粒が驚異的な速さで落下してこないことの説明になります.)
さて,それではこれだけで満足せずに,速度が始めの状態から  という状態へどう変化していくのか,その過程を求めてみましょう.
という状態へどう変化していくのか,その過程を求めてみましょう.
速度の時間変化を求める
先ほど状況設定に従って,運動方程式を求めました.
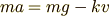
運動方程式は,物体がどんな運動を行うのか教えてくれます.この方程式を変形して,  は時間が経つにつれどう変化するのか求めましょう.
は時間が経つにつれどう変化するのか求めましょう.
加速度って…
運動方程式の左辺に加速度  が現れています.
加速度とは,ある時間が経って速度がどれだけの割合で変化したかを表す数字ですね.
つまり,時刻
が現れています.
加速度とは,ある時間が経って速度がどれだけの割合で変化したかを表す数字ですね.
つまり,時刻 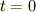 のときの速度を
のときの速度を  ,時刻
,時刻 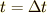 のときの速度を
のときの速度を 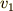 とすると,その間の加速度は,
とすると,その間の加速度は,

となります.これを時刻 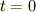 での加速度として,
での加速度として, 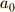 と書くことにしましょう.
と書くことにしましょう.
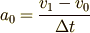
ということです.
さらに同じように,時刻 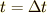 のときの加速度を
のときの加速度を 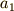 ,時刻
,時刻 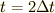 のときの加速度を
のときの加速度を 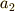 ,時刻
,時刻 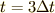 のときの加速度を
のときの加速度を 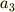 …というように考えていきましょう.
…というように考えていきましょう.
時刻は物体を落下させ始めてから測ることにします. 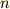 という文字は自然数を表すこととして,時刻
という文字は自然数を表すこととして,時刻  での状態まで,考えることにします.
での状態まで,考えることにします.

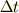 はかなり小さな値だと考えると,それぞれの時刻で運動方程式
はかなり小さな値だと考えると,それぞれの時刻で運動方程式 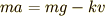 は同じ形で成立し続けます.ということは,
は同じ形で成立し続けます.ということは,
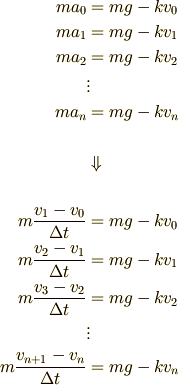
となります.
運動方程式を解きやすく変形
右辺に 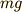 の部分があると計算を進めにくいので,
の部分があると計算を進めにくいので, 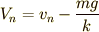 という書き方をしてみましょう.
上の式に
という書き方をしてみましょう.
上の式に 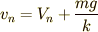 を代入してみます.すると,
を代入してみます.すると,
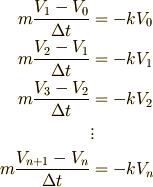
いくらか,すっきりした形になりました.
ここでさらに,両辺に 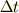 を掛け算して,
分母から
を掛け算して,
分母から 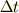 をなくしてしまいましょう.
をなくしてしまいましょう.
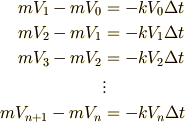
さらに少し整理すると,
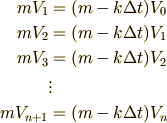
となりますね.数列を勉強した方は,この式を見て,等比数列になっていることに気づけるのではないでしょうか.
等比数列の一般項を求める
いま求めたばかりの式,両辺を 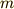 で割ります.
で割ります.
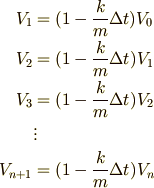
これらの式で,1つ目の式を2つ目の式に代入してみましょう.すると,
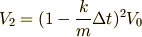
ということがわかりますね. これをさらに3つ目の式に代入してみると,
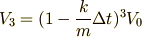
となります. さあ,これを最後の式まで繰り返していったらどうなるか…というと,
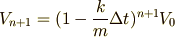
となります.
…って,そもそも求めたかったのは,  の時の速度
の時の速度  でしたから,
でしたから, 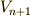 は行き過ぎですね.ひとつ戻って
は行き過ぎですね.ひとつ戻って  は,
は,
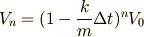
と求まります.
ちなみに 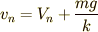 としていたのだから,
としていたのだから,
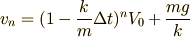
となりますね. この段階でも,もう一般の時刻での速度がわかった!と考えることもできます. [‡]
だけどせっかくなので,もう少し現代風の見慣れた形にしていきましょう.
| [‡] | Newtonがその著書「プリンキピア」で示した空気抵抗がある場合の解は,だいたいこのような形だったそうです. |
最後に極限操作を
いま速度を求めたい時刻を  としていますね.
つまり,
としていますね.
つまり, 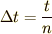 ということ.
ある時刻
ということ.
ある時刻  までを
までを  等分して,解析しているということです.
等分して,解析しているということです.
その結果として,時刻 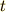 での速度
での速度  は,
は,

となるのでした.
Newtonの運動方程式は, 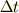 が小さいときに成立すると考えられているわけです.ですから,ここで
が小さいときに成立すると考えられているわけです.ですから,ここで 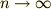 の極限をとりましょう.
の極限をとりましょう.
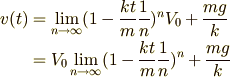
ですね.ここに現れる極限操作の部分, 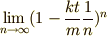 って,どこか見覚えがありませんか?
ここで,自然定数
って,どこか見覚えがありませんか?
ここで,自然定数  という書き方を思い出しましょう.
次のように定義される極限値を,特別に
という書き方を思い出しましょう.
次のように定義される極限値を,特別に  (自然定数)という文字で書き表すという約束事をしているのでした.
(自然定数)という文字で書き表すという約束事をしているのでした.
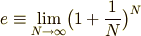
この極限値にそっくりの形が出てきていますね. 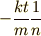 をまとめて,
をまとめて, 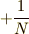 と思ってしまいましょう.
と思ってしまいましょう. 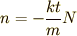 ということです.すると,
ということです.すると,
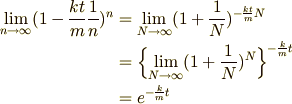
となります.このことを考えると,
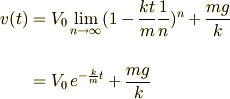
という結果になります.
最後に 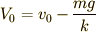 としていたことも思い出して,
としていたことも思い出して,
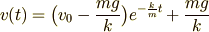
という式を得ます.これで,すっかり現代風の書き方になりました.
速度は指数関数 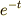 で,
で, 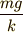 という値に近づいていくのです.
という値に近づいていくのです.
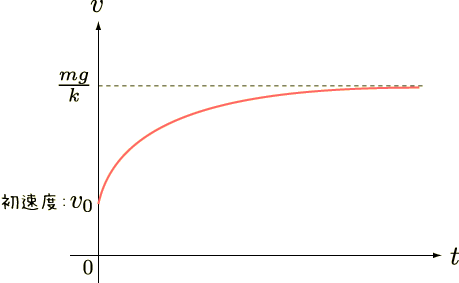
図は 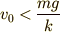 のとき.
だんだん落下速度は速くなり,
のとき.
だんだん落下速度は速くなり, 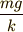 に近づいていく.
に近づいていく.
なにをやっていたのか
微分方程式を解いて求めた速度の式と同じ式を,微分方程式を解かずに求めることができました.これはすごいことだ!と思うでしょうか?
ミソは 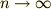 という操作にあります.
という操作にあります.
ここで行った解法では, 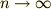 という操作をしても,等比数列で求めた
という操作をしても,等比数列で求めた 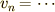 の式は成立し続ける…という信念を抱いています.
そして,Newtonの運動方程式:
の式は成立し続ける…という信念を抱いています.
そして,Newtonの運動方程式: 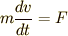 というものも,有限の(微小な)時間間隔で成り立っていた
というものも,有限の(微小な)時間間隔で成り立っていた 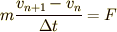 という関係が
という関係が 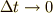 の極限でも成り立ち続けるという信念を用いて,書き表したものなのです.
の極限でも成り立ち続けるという信念を用いて,書き表したものなのです.
ここで行った解法も微分方程式を用いる解法も,同じ信念に基づいているので,どちらも同じ形になるのです.
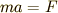 は
は の部分は重力
の部分は重力 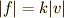 を足し算したものです.
力の向きに注意しましょう. 重力は下向きだから,正.
空気抵抗は速度と逆向きにかかります.だから
を足し算したものです.
力の向きに注意しましょう. 重力は下向きだから,正.
空気抵抗は速度と逆向きにかかります.だから 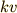 の前にマイナス符号がついています.なお
の前にマイナス符号がついています.なお