ベクトルの回転
ある軸の回りに,グルリとベクトルを回転させるとどうなるかを考えます.ベクトルの計算としては,内積,外積,ベクトルの射影が出てきます.忘れてしまった人は先に もう一度ベクトル を復習してみて下さい.最初に有限回転(回転の大きさが無視できない)の場合を考えます.次に,有限回転の式から微小回転(回転が十分小さい)の場合の式を導きます.この二つの式を導くのが本稿の目的です.
ベクトルの有限回転
ベクトル  を,
を,  と並行ではない単位ベクトル
と並行ではない単位ベクトル 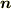 の回りに,角度
の回りに,角度 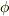 だけ回転させたものを
だけ回転させたものを  とします.回転の方向はネジを回すとベクトル
とします.回転の方向はネジを回すとベクトル 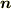 の方向にネジが進むような方向です.つまりは,次の図のような状況を考えているわけです.目標は,
の方向にネジが進むような方向です.つまりは,次の図のような状況を考えているわけです.目標は,  を
を  ,
, 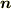 ,
, 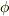 で表すことです.頑張りましょう.
で表すことです.頑張りましょう.
この図さえ綺麗に書ければ,半ば勝負はあったようなものです.  は次のように表すことが出来ます.図を見ながら,式を一行ずつ納得して読んで行って下さい.
は次のように表すことが出来ます.図を見ながら,式を一行ずつ納得して読んで行って下さい.
![\bm{r'}&=\overrightarrow {ON}+\overrightarrow {NV}+\overrightarrow {VQ} \\&=\bm{n}(\bm{n}\cdot \bm{r})+[\bm{r} - \bm{n} (\bm{n}\cdot \bm{r})]\cos \phi -(\bm{r}\times \bm{n})\sin \phi \tag{1}](./459471e29709f94966ec921123e4a276.png)
一気に最後まで書いてしまいましたが,ここでの計算は大丈夫でしょうか.途中で,ベクトルの射影と外積を使っています.一応,何がどうなっているのか,説明をしておきましょう.
[式の解説]
一行目はさすがに大丈夫だと思います.
二行目を一項ずつ見ていきましょう.まず 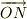 ですが,これは
ですが,これは  を
を  に射影したものですので
に射影したものですので 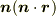 となるわけです.
となるわけです.  は単位ベクトルなので長さは
は単位ベクトルなので長さは 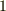 だということに注意して下さい.(ベクトルの射影を忘れてしまった人は, もう一度ベクトル を復習して下さい.)
だということに注意して下さい.(ベクトルの射影を忘れてしまった人は, もう一度ベクトル を復習して下さい.)
次にベクトル 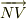 ですが,これはベクトル
ですが,これはベクトル 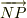 と向きが同じで,長さは
と向きが同じで,長さは 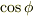 倍のものですので(上図の右側を見てください),
倍のものですので(上図の右側を見てください), ![\overrightarrow {NP} \cos \phi = [\overrightarrow {OP}-\overrightarrow {ON}] \cos \phi = [\bm{r} - \bm{n} (\bm{n}\cdot \bm{r})]\cos \phi](./d0692e6b98bd6c3421ce5003ccee7866.png) と書けるわけです.
と書けるわけです.
最後にベクトル 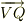 ですが,これが
ですが,これが 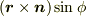 だというのには,少し説明が要るかもしれません.まず外積の定義を思い出しましょう.外積
だというのには,少し説明が要るかもしれません.まず外積の定義を思い出しましょう.外積 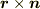 の向きは,ねじ回しを,ベクトル
の向きは,ねじ回しを,ベクトル  からベクトル
からベクトル 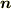 に向かって回したときに,ネジが進む方向でした.つまり,右の図に書いてあるような向きになります.また,その大きさは
に向かって回したときに,ネジが進む方向でした.つまり,右の図に書いてあるような向きになります.また,その大きさは  と
と 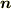 のなす角を
のなす角を  とすれば
とすれば  でしたので,ちょうど図に描いてある円の半径と等しくなるわけです.
でしたので,ちょうど図に描いてある円の半径と等しくなるわけです.  は左の図に書き込んでありますので,
は左の図に書き込んでありますので, 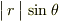 が図の円の半径に等しくなることを確認して下さい.
が図の円の半径に等しくなることを確認して下さい. 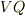 の長さは円の半径の
の長さは円の半径の  倍ですから,
倍ですから, 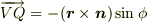 となるわけです.(
となるわけです.( 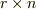 と
と 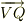 は向きが逆なのでマイナスがついていることにも注意して下さい.)
は向きが逆なのでマイナスがついていることにも注意して下さい.)
[式の解説終わり]
式(1)は『ベクトル  を,ベクトル単位ベクトル
を,ベクトル単位ベクトル 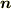 の回りに半時計回りに角
の回りに半時計回りに角 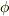 だけ回転させた』ベクトル
だけ回転させた』ベクトル  を表す式だということです.これはロドリグの公式と呼ばれています.少しだけ項のまとめ方を変えて,次のような形で紹介されていることの方が多いかも知れません.
を表す式だということです.これはロドリグの公式と呼ばれています.少しだけ項のまとめ方を変えて,次のような形で紹介されていることの方が多いかも知れません.
![\bm{r'}=\bm{r}\cos \phi+ \bm{n} (\bm{n}\cdot \bm{r})[1-\cos \phi] -(\bm{r}\times \bm{n})\sin \phi \tag{2}](./a556aef206dd525334e6df116aa87264.png)
無限小回転
さきほど求めたロドリグの公式で,回転が微小の場合を考えましょう.式(2)で, 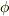 の代わりに
の代わりに 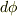 とします.このとき
とします.このとき 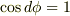 ,
,  とみなせますので,式(2)は次のような簡単な形に帰着してしまいます.
とみなせますので,式(2)は次のような簡単な形に帰着してしまいます.
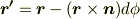
回転が微小のときにはベクトル  の変化も微小だと考えて,
の変化も微小だと考えて, 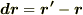 と置くと,次のように書けることが分かると思います.
と置くと,次のように書けることが分かると思います.
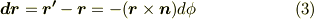
これがベクトルを微小回転させたときの変位を表す式です.教科書によっては,この式がいきなりベクトルの微分というページに出てくることもあります.それはそれで一つの考え方です.本稿では,敢えて,図形的に有限回転の場合をまず求め,そこから無限小回転の場合を導くというアプローチを取りました.
回転する座標系から運動を見るときに,遠心力,コリオリ力などの見かけの力が働きますが,こうした見かけの力を求めるときに式(3)がとても大事です.
まとめ
公式としてベクトルの回転の式を再掲しておきます.ときには有限回転の式も重要です.
有限回転の式:
![\bm{r'}=\bm{r}\cos \phi+ \bm{n} (\bm{n}\cdot \bm{r})[1-\cos \phi] -(\bm{r}\times \bm{n})\sin \phi \tag{2}](./a556aef206dd525334e6df116aa87264.png)
微小回転の式:

注)有限回転の式を,ロドリグの公式と呼びましたが,この式を導いたのはロドリグではないという説が有力です.この式自体は,実はもっと昔から知られていたようなのですが,ベクトルという概念がまだ無かったので,違った説明のされかたをされていました.ベクトルという概念を前面に押し出して,この公式を初めて導いたのはギブスのようです.こういった事情により,ロドリグの公式という言い方を避けて,ベクトルの回転公式などと呼ぶ人もいるようですが,未だに定着している名前はありません.本稿では,慣用に従ってロドリグの公式という名前を使いました.