ベクトル方程式
1.ベクトル方程式とは
ベクトル方程式とは空間上の点がある規則(直線上,平面上,円上,球上にあるetc)をベクトルで表現しようと言う主旨のものです. 僕たちが中学で習った一次関数の式

も変形してあげれば

のように
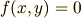
というように方程式の形で表せます. 一次関数のグラフのような二次元上の簡単な図形であればベクトルを用いなくても比較的に簡単にその座標の組が満たす方程式が立てられます. しかしそれが,曲線となったり三次元上の点となるとなかなか一筋縄ではいきません. そこでベクトル幾何学的な性質などを利用して,ベクトルでその点の満たすべき方程式を立てるのです.
今一度"方程式"の用語の意味を確認しておきましょう. 方程式とは
Important
「"ある"変数について成り立っている等式」
のことを言います. これは僕の捉え方ですがいわゆる「関係式」という解釈をしてあげると一番感覚的に納得しやすいと思います. そのベクトルが満たさなければならない条件をベクトルに含まれる量を用いて関係式を立ててあげればいいのです.
2.直線の方程式
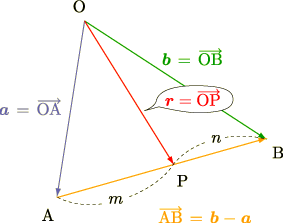
先ず直線のベクトル方程式を考えて見ましょう. 図形的に考えると以下の通り
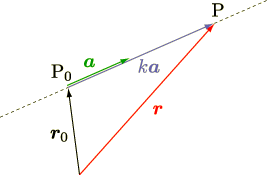
ここでの表現を数式を用いて表すと適当な実数を  一般の位置ベクトルを
一般の位置ベクトルを  として
として
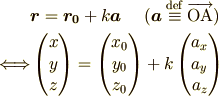
各成分を比較して
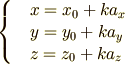
上式の 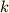 はパラメタなので消去(
はパラメタなので消去( 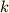 について解いて三式を
について解いて三式を  で結ぶ)すると
で結ぶ)すると
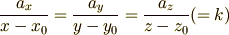
とした上式が正式な三次元の直線の方程式です.この  と
と 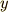 についての等式だけを変形すると
についての等式だけを変形すると
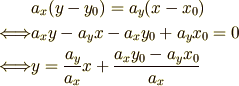
となり
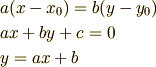
という二次元の直線の方程式と一致することが見て取れるかと思います. 具体的には三次元の直線の方程式を二次元の座標に射影させた直線とも見ることが出来ます.
直線の方程式は直線が通る二点がわかっていれば, もう一度ベクトル3 の内分点のところにある表記で表すこともできます.
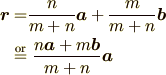
3.平面の方程式
- 型1 平面上の2ベクトルがわかっている場合
平面上に乗っている2ベクトルが既知の場合を考えます
平行でない2ベクトル 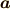 ,
, 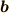 の各定数倍の和(数学的には線形結合
とか一次結合と言います):
の各定数倍の和(数学的には線形結合
とか一次結合と言います): 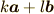 がそのベクトルの乗っかっている
平面全てを表せるという事です.
がそのベクトルの乗っかっている
平面全てを表せるという事です.
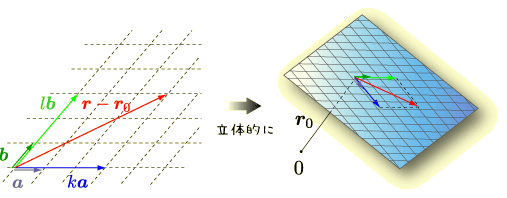
上図のように平面上のあらゆる点が 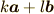 で表せることは納得して
いただけるでしょうか?
で表せることは納得して
いただけるでしょうか?
因みに上図は 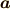 ,
, 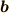 を基底とした斜交座標と言います.
「平行でない」をことわった理由は斜交座標では基底が平行だとどちらを実数倍しても
基底方向の直線しか表せず,平面を表現できないために平行でない場合を前提に議論を
したかったからです.その様子も上図から見て取れると思います.
を基底とした斜交座標と言います.
「平行でない」をことわった理由は斜交座標では基底が平行だとどちらを実数倍しても
基底方向の直線しか表せず,平面を表現できないために平行でない場合を前提に議論を
したかったからです.その様子も上図から見て取れると思います.
平面上の任意のベクトルを  とすると上記の2ベクトルの線形結合で表せるので
とすると上記の2ベクトルの線形結合で表せるので
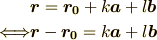
ここで計算を簡単にするため  を
考えます
を
考えます
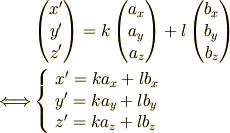
とかけました.今回はパラメーターが二つあるのでうまく消去するのは難しいですので ここで計算はストップしておきましょう.
- 型2 平面に垂直なベクトルがわかっている場合
平面に垂直なベクトルがわかっている場合を考えます 以上のようにその平面に乗っている2ベクトルがわかればよいのですが,たいていの 問題ではその平面に垂直なベクトル(法線ベクトル)を考えて計算します.なぜなら1つの 平面と一対一に対応するのはその平面に垂直なベクトルだからです.ためしに紙にペンの 背中をつけてグリグリ立体的にまわしてみますと一対一に対応していることが見て取れるか と思います.また,物理的にその点での物理的状態を考える際にも法線を使うことが関係し ています.

具体的に計算をするのですが,上図から 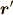 と
と 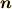 の内積を取れば
即解決します.具体的に書きますと
の内積を取れば
即解決します.具体的に書きますと
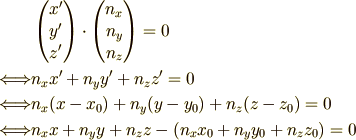
ということで一般化しますと
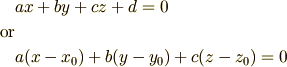
は法線ベクトルが

の適当な定点(〜式であれば 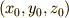 )を通る平面の方程式の一般形であること
がわかると思います.型1のような与えられ方をしていてもその2ベクトルの外積から
法線ベクトルを求めればすぐに公式どおりの計算に持ち込めるはずです.また,この法線
ベクトルは単位法線ベクトルである必要性はありません.なぜなら法線ベクトルを
,
)を通る平面の方程式の一般形であること
がわかると思います.型1のような与えられ方をしていてもその2ベクトルの外積から
法線ベクトルを求めればすぐに公式どおりの計算に持ち込めるはずです.また,この法線
ベクトルは単位法線ベクトルである必要性はありません.なぜなら法線ベクトルを
, 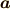 その大きさを
その大きさを 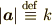 とし,法線
ベクトルに平行な単位法線ベクトルを
とし,法線
ベクトルに平行な単位法線ベクトルを 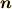 とすると
とすると

となります.ここで直線の方程式に代入してみますと
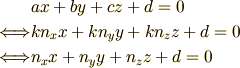
となり全ての 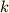 が約分されるので単位ベクトルでもそうでなくても向きさえあっていれば
全く同値な式が導けます.
が約分されるので単位ベクトルでもそうでなくても向きさえあっていれば
全く同値な式が導けます.
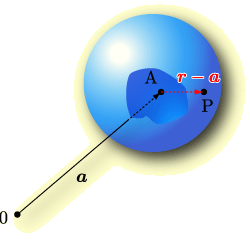
4.球面の方程式
球面であるとはどういうことでしょうか?「ある定点までの距離が一定」と言った
事実からベクトル  が満たすべき条件は球の中心を
が満たすべき条件は球の中心を 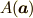 ,
半径を
,
半径を  として
として
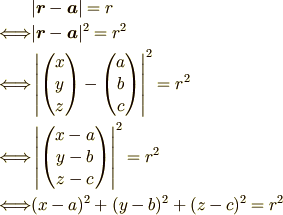
円の方程式はと言うと二次元の円であれば 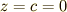 として
として
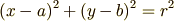
と表せます.
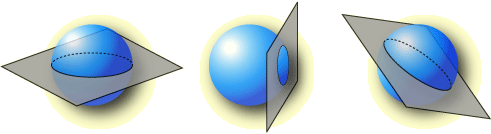
立体的に傾いた円であれば球の方程式と平面の方程式の共通部分の解集合として与えられるので原理的には2つの方程式を連立してあげればよいのではないでしょうか. でも手で解くのは結構大変そうですね.
5.円錐の方程式(演習問題)
以上のことから円錐の方程式も比較的容易にわかるのでぜひ挑戦してみましょう
因みに一般系は,円錐の頂点の位置ベクトルを  として
として
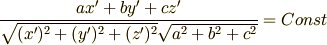
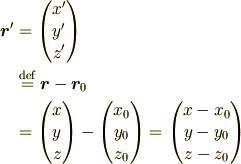
と表せます. もちろん他の文献では,これを変形したものや,定数を置き換えて体裁を整えたものが載っているかもしれません. 解答は準備中.
hint
- 角度の概念が出てきます
- 表記を睨んで見ましょう
6.まとめ
ベクトル方程式を自分で立てるのにはちょっとしたコツがいるかもしれません. ベクトルが持つ幾何学的な条件の中で"どれ"を使うかがキーになってきます.
- 直線の方程式…ベクトルのスカラー倍でベクトルを延長した際に,直線を表せること,つまりベクトルが線分(直線≠曲線)であること.方向という量を表せること
- 平面の方程式 型1…2つのベクトルの線形結合で1つの平面が決定できること,つまり方向の違う直線により,その2つの直線が張る平面が一意的に決められること.
- 平面の方程式 型2…平面と一対一に対応するものとして法線があること.その法線をベクトルで表せること.平面上の任意の点を表すベクトルと法線ベクトルが直交するという幾何学的条件を内積により表せること.
- 球の方程式…ベクトルが線分である(あるいは大きさがある)ということ.
- 円錐の方程式…内積により角度が表現できること.
と挙げてみるとどうやら
- 線分→延ばすと直線
- 線分→大きさがある
- 方向&内積→2つのベクトル間の角度が表せる
といった点に集約されるのではないでしょうか. 逆に以上の条件では表し難い図形,例えば楕円体などはコンパクトなベクトル方程式では表せないかもしれません. ベクトル方程式も万能とはいえませんが,表せる図形がコンパクトな表式であれば機械的な計算で,図形の方程式を導くことが出来ます.