ベクトル解析奮闘記1
はじめに
講義などで初めてベクトル解析を習った時,“難しい”,“わけわからん”と思った経験がありませんか?実は私もその一人です.いまだに詳しくはわかりませんが,これまで私が悩んだ過程をここにご紹介して,もしご参考になればと思います.
初講義前日
ベクトル解析って,ベクトルを使って問題解いたりするのでしょうか?ベクトルなら高校の数学で習ったし,要するに大きさと,方向(向き)を持つ概念ですよね?矢印作図して足し算したり,引き算したり,大きさを実数倍したり,特に始点を原点
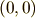
にすれば終点の座標 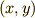 でベクトルを表せちゃいます.作図しなくても,そういう風に成分表示すれば足し算,引き算も簡単です.内積だってわかります.成分で書くと
でベクトルを表せちゃいます.作図しなくても,そういう風に成分表示すれば足し算,引き算も簡単です.内積だってわかります.成分で書くと 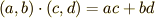 とすればいいのです.簡単,なはずです.
たいした事ないですよ,きっと.実は明日ベクトル解析の初講義なんですが,予習なんてしないで寝ちゃおっと・・・.
とすればいいのです.簡単,なはずです.
たいした事ないですよ,きっと.実は明日ベクトル解析の初講義なんですが,予習なんてしないで寝ちゃおっと・・・.
翌日初講義終了.ところが!
わー,なんなんだこれは!
わからん,全くわからん!だいたい三角関数の 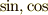 じゃあるまいし,なんで
ベクトルやるのに3,4文字英単語(
じゃあるまいし,なんで
ベクトルやるのに3,4文字英単語(  (グラジエント),
(グラジエント), 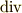 (ダイバージェンス),
(ダイバージェンス), 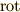 (ローテーション))や,おまけに偏微分記号まで出てくるんでしょう!もちろん
(ローテーション))や,おまけに偏微分記号まで出てくるんでしょう!もちろん 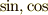 は私でもわかります,直角三角形の辺の比ですよね?(絵を書いてみればすぐわかります.)偏微分だって,他の変数(例えば
は私でもわかります,直角三角形の辺の比ですよね?(絵を書いてみればすぐわかります.)偏微分だって,他の変数(例えば  で微分する場合,それ以外の
で微分する場合,それ以外の 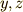 など)を定数と見て,微分する事でしょ?それも知ってるんだがなあ.いずれにせよこれは家に帰ってよく復習しないと.電磁気学はこれ使うって言うし・・・.
など)を定数と見て,微分する事でしょ?それも知ってるんだがなあ.いずれにせよこれは家に帰ってよく復習しないと.電磁気学はこれ使うって言うし・・・.
自宅で復習(gradの巻)
ここであきらめたり,あせってもしょうがないのでまずゆっくり順番に考えてみました.
"  "はえーっと"
"はえーっと" 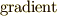 (傾き)"の略ですか・・・.たしか先生が黒板に書いた式は
(傾き)"の略ですか・・・.たしか先生が黒板に書いた式は
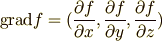
だったなー.
う〜ん,  ももちろん,
ももちろん, 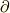 がいかにも難しそう・・・.でも冷静に見ると,これは値が三つ組みになってるから,スカラー(ベクトルのように方向を持たないただの数値)関数
がいかにも難しそう・・・.でも冷静に見ると,これは値が三つ組みになってるから,スカラー(ベクトルのように方向を持たないただの数値)関数 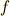 から3次元のベクトルを一つ作ったようですね(どんなベクトルかはまだわかりませんが).とりあえず,わかりやすくするために
から3次元のベクトルを一つ作ったようですね(どんなベクトルかはまだわかりませんが).とりあえず,わかりやすくするために  を省いて2次元で考えると
を省いて2次元で考えると
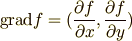
あれっ,こうやってみると,  の変化に対する
の変化に対する 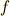 の変化率と,
の変化率と, 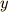 の変化に対する
の変化に対する 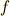 の変化率を
の変化率を 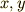 成分に持つベクトルのようですね.例えば
成分に持つベクトルのようですね.例えば 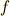 を具体的に考えると
を具体的に考えると
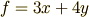
なら
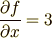
( 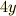 は定数扱いで
は定数扱いで 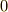 になる)
になる)
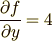
( 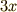 は定数扱いで
は定数扱いで 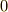 になる)だから
になる)だから
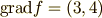
となるわけですか・・・.
一体このベクトルは何者でしょうか?
今の場合,変数 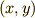 の変化に対する
の変化に対する 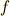 の変化率を表記する時に,
の変化率を表記する時に,  方向に対する変化率は
方向に対する変化率は 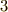 ,
, 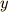 方向に対する変化率は
方向に対する変化率は 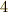 ,ということなのですが,どちらか
,ということなのですが,どちらか 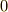 なら,片方だけ(数値1個)で表されるのでしょうけど,実際はそうとは限らないし,
なら,片方だけ(数値1個)で表されるのでしょうけど,実際はそうとは限らないし,  方向と
方向と 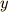 方向じゃ違う方向の大きさですから,
方向じゃ違う方向の大きさですから, 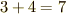 と足し算するわけにもいきません.もし
と足し算するわけにもいきません.もし 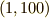 なら,ほとんど
なら,ほとんど 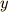 方向と考えていいけど,
方向と考えていいけど,  方向も完全に無視はできないし,それぞれの方向の大きさに応じた合成方向・・・というわけですか.この数値の場合と,一般的な場合をグラフに書くと以下のようになりますね.
方向も完全に無視はできないし,それぞれの方向の大きさに応じた合成方向・・・というわけですか.この数値の場合と,一般的な場合をグラフに書くと以下のようになりますね.
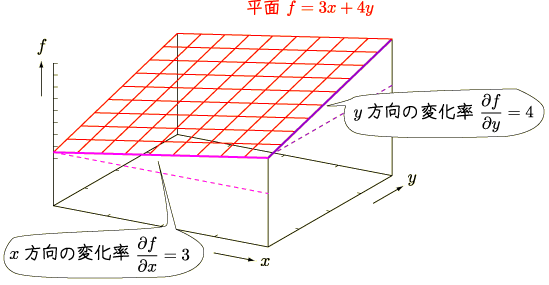
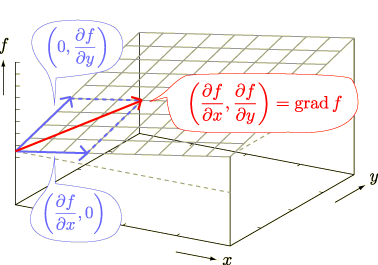
なるほど,それで  方向と
方向と 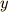 方向の変化率をそれぞれ
方向の変化率をそれぞれ  方向と
方向と 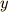 方向の成分としたベクトル
方向の成分としたベクトル
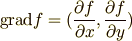
を考えれば,まとめて表記できるわけですね.  方向の変化率を
方向の変化率を
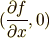
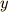 方向の変化率を
方向の変化率を
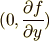
と,それぞれ自体ベクトルと考えると,
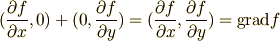
ですから, 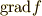 は
は  の変化率と
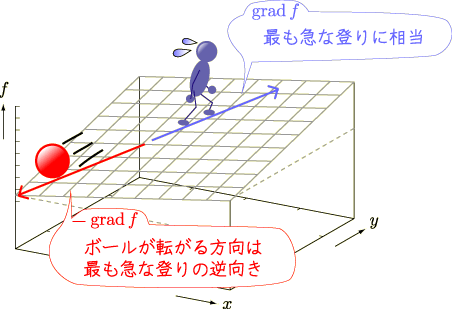
の変化率と 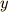 の変化率を方向も含めて合成した,一番変化率の高い(坂で言えば勾配のきつい)方向を向いてるベクトルなんですね.だから
の変化率を方向も含めて合成した,一番変化率の高い(坂で言えば勾配のきつい)方向を向いてるベクトルなんですね.だから  (勾配)というのか・・・.ふー,やっとわかった気がします.(
(勾配)というのか・・・.ふー,やっとわかった気がします.(  を増やして3次元で考えても同じ事ですね)
を増やして3次元で考えても同じ事ですね)
勾配がきつい方向ということは,矢印を逆にすれば,ボールが転がり落ちてくる方向になります(下図).