三角比
物理,いや物理に限らずカガク的なことをやっていると,
当然のように 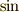 (サイン),
(サイン), 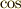 (コサイン),
(コサイン), 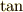 (タンジェント)
という三角比(三角関数)が登場します.使っているととっても当たり前,とっても便利.
しかし知らないとどうしようもない.
(タンジェント)
という三角比(三角関数)が登場します.使っているととっても当たり前,とっても便利.
しかし知らないとどうしようもない.
高校時代,変な公式に惑わされ,サインやコサインが出てくる理由が イマイチよく分からなかった方も多いのではないかと思います. しかしこれらは慣れるととても便利です.だからこそいつも出てくるんですね.
まず,下の図を見てみて下さい.
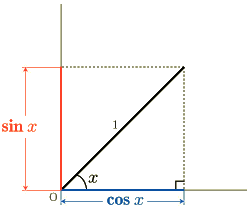
三角比で大切なのはこの関係でほぼすべてです.
直角三角形があったとき,下側が 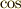 ,高さが
,高さが 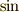 です.
簡単でしょう? 何も難しいことなどありません.
これで十分なのですが,心もとないので以下に詳しい説明も書いておきます.
です.
簡単でしょう? 何も難しいことなどありません.
これで十分なのですが,心もとないので以下に詳しい説明も書いておきます.
三角比の定義
三角比の仕事は,直角三角形の辺を角度を使って対応づけることです.
まず,直角三角形の直角でない角度の1つを  としておきます
(普通は角度の変数に
としておきます
(普通は角度の変数に  (シータ)が使われますが,別に記号は何でもいいので
(シータ)が使われますが,別に記号は何でもいいので  にしときます).
このとき三角形の各辺がどういう名前で呼ばれるのか覚えておきましょう.下のようになっています.
にしときます).
このとき三角形の各辺がどういう名前で呼ばれるのか覚えておきましょう.下のようになっています.
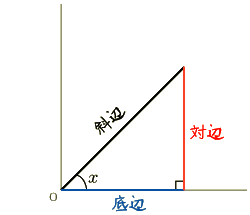
このように,角度  がくっついている辺の,
直角が付いている方を底辺,そうでない方を斜辺と呼びます.
冒頭の説明で「下側」といったのは底辺のことです.
がくっついている辺の,
直角が付いている方を底辺,そうでない方を斜辺と呼びます.
冒頭の説明で「下側」といったのは底辺のことです.
 の反対側の辺は対辺と呼びます.三角比の定義はつぎのようになってます.
の反対側の辺は対辺と呼びます.三角比の定義はつぎのようになってます.
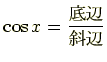
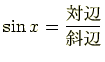

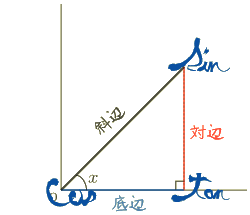
って,これじゃあ教科書の説明となんら変わりがありませんね. でもこれは定義なので,はじめは覚えなきゃどうしょうもない部分であります.
斜辺と角度で底辺と対辺を表す
三角比の基準になるのは斜辺です.斜辺(の長さ)と角度  を使って底辺,対辺を表すことができます.
上で紹介した定義で,
を使って底辺,対辺を表すことができます.
上で紹介した定義で, 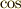 と
と 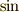 の式の両辺にそれぞれ斜辺を掛けてみましょう.すると
の式の両辺にそれぞれ斜辺を掛けてみましょう.すると


となります.ここで斜辺の長さを  としています.
長さ,と言いましたが,斜辺の単位は m(メートル = 長さ)でも
m/s(メートル毎秒 = 速度)でもなんでもかまいません.
としています.
長さ,と言いましたが,斜辺の単位は m(メートル = 長さ)でも
m/s(メートル毎秒 = 速度)でもなんでもかまいません.
このとき,底辺と対辺はつぎのように表せます.
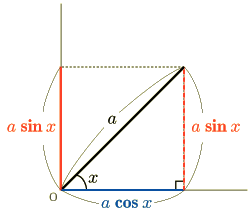
底辺が 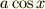 ,対辺が
,対辺が 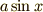 です.
このとき対辺は縦軸に相当するので,図のように軸の高さと考えていいです.
つまり
です.
このとき対辺は縦軸に相当するので,図のように軸の高さと考えていいです.
つまり 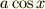 が横軸,
が横軸, 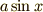 が縦軸を表しています.
が縦軸を表しています.
また, 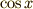 や
や 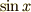 は
は  によって値が変わります.
下の図を見てください.斜辺の大きさは 1 としています.
によって値が変わります.
下の図を見てください.斜辺の大きさは 1 としています.
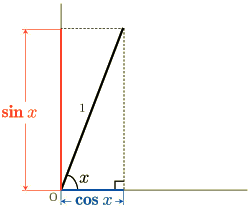
いままでより  を大きくしています.このとき
を大きくしています.このとき 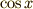 は小さく,
は小さく,
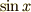 は大きくなっています(0度 <
は大きくなっています(0度 <  < 90度 の場合です).
逆に
< 90度 の場合です).
逆に  を小さくすると下のようになります.
を小さくすると下のようになります.
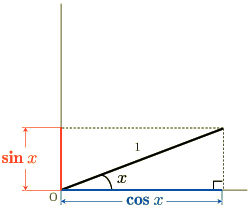
今度は 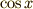 が大きく,
が大きく, 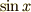 は小さくなりました.
三角比はこのように,直角三角形のどれか一つの辺と角度を基準にして,
ほかの辺を表すものです.そしてより一般的に拡張し,関数にしたものが三角関数です.
は小さくなりました.
三角比はこのように,直角三角形のどれか一つの辺と角度を基準にして,
ほかの辺を表すものです.そしてより一般的に拡張し,関数にしたものが三角関数です.
物理での例
物理でよく三角比をつかう例として,速度を  方向と
方向と 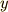 方向に分解するものを上げます.
方向に分解するものを上げます.
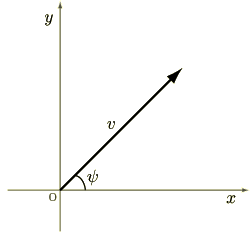
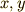 の2次元座標でつぎのような斜め方向の速度
の2次元座標でつぎのような斜め方向の速度  があったとしましょう.
があったとしましょう.
 軸となす角は
軸となす角は 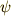 (プサイ)としています.
(プサイ)としています.
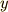 方向を垂直座標,
方向を垂直座標,  方向を水平座標であるとすると,
速度
方向を水平座標であるとすると,
速度  は斜めに投げ上げた速度に相当します(
は斜めに投げ上げた速度に相当します( 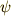 は仰角と呼ばれます).
この斜め方向の速度を,三角比を使って垂直成分と水平成分に分解することができます.
分解するとつぎのようになるのは,すぐ分かりますよね.
は仰角と呼ばれます).
この斜め方向の速度を,三角比を使って垂直成分と水平成分に分解することができます.
分解するとつぎのようになるのは,すぐ分かりますよね.
速度の垂直成分 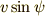 は重力による力を下向きに受けますから,
時間が経つと
は重力による力を下向きに受けますから,
時間が経つと 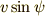 は減速し,あるところで止まって,
今度は逆向きの速度になり,下に落ちてきます.
速度の水平成分
は減速し,あるところで止まって,
今度は逆向きの速度になり,下に落ちてきます.
速度の水平成分 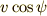 は空気抵抗を考えない限り力を受けないので,等速直線運動を続けます.
は空気抵抗を考えない限り力を受けないので,等速直線運動を続けます.
このように三角比を使って速度を水平と垂直に分解することで, 一見複雑そうな斜めの速度を別々に,簡単に考えることができるって寸法です.