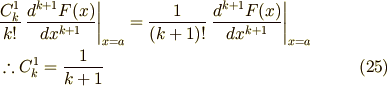和と積分との関係
積分される物理量が発散しないかぎり,その積分によって特徴付けられる物理量は,本質的にはある特別な和の極限として定義できます. 積分の定義を理解する事によって,実用的にも計算の幅が広がります.そこで,ここでは次の2つの事を説明します.
- 微分の逆演算としての積分
- 積分と和との差を埋める規格化因子
目標としては,1.で解析的に性質の良い関数(以下,なめらかな関数とここでは呼びます)について一般に成り立つ積分(リーマン積分)の定義を理解する事. 次に2.で和と積分との関わりを調べ,「和の極限が積分」だという思考の短絡を起こさないようにする事としています. なお,この番号はセクション番号に対応しております.
1.微分の逆演算としての積分
よく「微分と積分は逆演算だよ」と高校生の頃から教えられてきていると思います.まさにその通りで,物理で使うときも多くの場合, 微分の逆の効果を期待して積分を使っています.例えば速度が分かっているときに,加速度を知りたければ微分をつかって求めます. ではその逆の場合は何をしますか.そう,加速度を積分するのです.このセクションではまず積分と微分との関わりを明確にする事を 目標とします.次に和について確認をし,次の規格化因子の話へつなげたいと思います.
微分の逆演算としての積分
積分を微分の逆演算であるとして定義していきます.
1変数関数 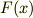 の導関数を
の導関数を 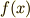 とします.次のように変数
とします.次のように変数  に番号付けをしておきます.
に番号付けをしておきます.
![&x_{0} = a <x_{1}<x_{2}< \cdot\cdot\cdot <x_{n} = b <x_{n+1} \tag{1}\\&\xi_{i} = x_{i-1} + \theta \Delta_{i} [0 < \theta < 1] \tag{2}\\& \Delta_{i} = x_{i} - x_{i-1} [i= 1,2,3,\cdot\cdot\cdot ,n+1] \tag{3}\\&|\Delta| \equiv \{ \Delta_{max} | \Delta_{i} (i=1,2,3,\cdot\cdot\cdot ,n+1) \} \tag{4}](./09d379923fc6120ce6db686983c815d0.png)
ここで書いた 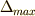 とは分割の最大の大きさで,
とは分割の最大の大きさで, 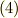 は「分割の大きさを最大値で評価しましょう」と言っているのです.
分割ゼロの極限をとりたいときには,
は「分割の大きさを最大値で評価しましょう」と言っているのです.
分割ゼロの極限をとりたいときには,  をゼロの極限をとれば良いです.
なぜならば大きさとして採用する
をゼロの極限をとれば良いです.
なぜならば大きさとして採用する  は常に
は常に 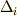 の中の最大値
の中の最大値 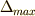 としているからです.
次に平均値の定理より次の事が言えます.
としているからです.
次に平均値の定理より次の事が言えます.
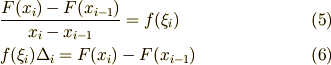
ここで更に 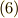 の両辺の和をとると
の両辺の和をとると
![\sum_{i=1}^{n+1} [F(x_{i}) -F(x_{i-1})] &= [F(x_{n+1}) -F(x_{n})] +[F(x_{n})-F{x_{n-1}}] + \cdot\cdot\cdot + [F(x_{2}) - F(x_{1})] +[F(x_{1})-F(x_{0})] \\ &= F(x_{n+1}) -F(x_{0}) = F(b+\Delta_{n+1}) - F(a) \\ &= F(b) - F(a) + \sum_{k=1}^{\infty} \frac{1}{k!} \left.\frac{d^{k}F}{dx^{k}}\right|_{x=b} \Delta_{n+1}^{k}](./1fcc2ae0525ec600092bc6fecb8cc836.png)
になります.上の式を整理しておくと,次のように書けます.
![\sum_{i=1}^{n+1} [\Delta_{i} f(\xi_{i})] = F(b) -F(a) + \sum_{k=1}^{\infty} \frac{1}{k!} \left.\frac{d^{k}F}{dx^{k}}\right|_{x=b} \Delta_{n+1}^{k} \tag{7}](./571bb200c4d9319b715a95b38b2b167b.png)
ここで分割の大きさ 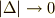 の極限をとります.すると
の極限をとります.すると 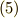 式は微分の定義式のかたちになります.
微分可能なとき次の式を満たす必要があります.
式は微分の定義式のかたちになります.
微分可能なとき次の式を満たす必要があります.

関数 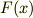 が
が 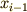 で連続ならば,
で連続ならば, 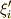 を
を 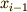 と書けます.そしてこのとき
と書けます.そしてこのとき 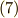 式は積分の定義式
式は積分の定義式
![&\lim_{|\Delta| \to 0} \sum_{i=1}^{n+1} [\Delta_{i} f(\xi_{i})] = \lim_{|\Delta| \to 0} \left[ F(b) -F(a) + \sum_{k=1}^{\infty} \frac{1}{k!} \left.\frac{d^{k}F}{dx^{k}}\right|_{x=b} \Delta_{n+1}^{k} \right] \\&\therefore \lim_{|\Delta| \to 0} \sum_{i=1}^{n+1} [\Delta_{i} f(\xi_{i})] = F(b) -F(a) \tag{9}](./9b74fc4e9fb530181da25fc81999aae4.png)
になります.なぜ積分の定義式と呼べるかと言うと,この 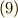 は微分の逆演算としての性能を満たしているからです.
それを説明するためにここで積分の始点を固定し,終点
は微分の逆演算としての性能を満たしているからです.
それを説明するためにここで積分の始点を固定し,終点 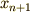 を変数
を変数 ![{x[a \le x \le b]}](./65fce9fa2d73d7803a364c305dfaa958.png) として積分するときを考えます.
すると
として積分するときを考えます.
すると  が任意であることに注意して(
が任意であることに注意して( 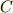 :任意定数)
:任意定数)
![\lim_{ |\Delta| \to 0 } \sum_{i=1}^{n+1} [\Delta_{i} f(\xi_{i})] = F(x) - F(a) = F(x) + C \tag{10}](./87a81b76f065870f259231929336bf25.png)
と書くことができます.この積分に対応した微分は 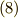 に
に 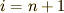 を代入したものです.
を代入したものです.
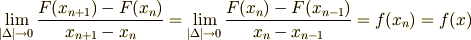
この  が導関数
が導関数 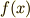 から逆に
から逆に 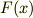 を求めていることから,
確かに微分の逆演算としての性能を満たしている事が確かめられました.これを積分と呼び,この量を簡単に次のように書くことにします.
を求めていることから,
確かに微分の逆演算としての性能を満たしている事が確かめられました.これを積分と呼び,この量を簡単に次のように書くことにします.
![\lim_{ |\Delta| \to 0 } \sum_{i=1}^{n+1} [\Delta_{i} f(\xi_{i})] \equiv \int_{a}^{b}dxf(x) \tag{A}](./c491e78a3eec1aacb167d1f0cfef94f3.png)
和について
積分が分かったところで,和について確認しておきます.
1変数関数 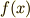 を離散的に閉区間
を離散的に閉区間 ![{[a,b]}](./5cfca6be945d8f0af86e25fc51bdf6c4.png) まで和をとったものは次のように書けます.
まで和をとったものは次のように書けます.

そうすると閉区間 ![{[a,b]}](./5cfca6be945d8f0af86e25fc51bdf6c4.png) の間で有限な十分に細かい分割での和は
の間で有限な十分に細かい分割での和は
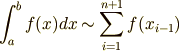
になるはずです.しかしながらこの和を分割の大きさ 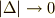 の極限は存在しません(詳しい計算はおまけとして最後に示してあります).
の極限は存在しません(詳しい計算はおまけとして最後に示してあります).
2. 積分と和との差を埋める規格化因子
規格化因子とは,和と積分の間の差を埋めるための因子のことを指します.
ここでは,積分する問題の計算を,修正された和の極限として求める事で,和と積分とのギャップを理解する事を目標とします.
具体的に規格化因子  のカタチを求めるには まず,和と規格化因子の積の極限として積分を作ります.
そして次に
のカタチを求めるには まず,和と規格化因子の積の極限として積分を作ります.
そして次に 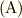 との比較すれば良いです.和と規格化因子の積の極限を数式で書くと,次のように書けます.
との比較すれば良いです.和と規格化因子の積の極限を数式で書くと,次のように書けます.
![\lim_{ h \to 0 } \left[ h(n) \sum_{i=1}^{n+1} f(x_{i-1}) \right] = \int_{a}^{b} dx f(x) \tag{12}](./bb6fbfc2e5efc66381e5bacda18b1939.png)
すると直ちに 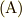 との比較により規格化因子
との比較により規格化因子  は
は
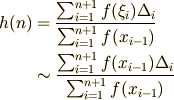
を満たす量だと言う事が分かります.2段目は近似的に成り立つのですが,この近似は極限をとることで等式で結ばれます. 積分へ移行するときに極限操作を行う事から規格化因子(和と積分に補正する因子)を簡単に次のように定義することができます.
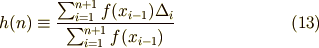
この簡単化のために後で極限をとらないと,いくらか規格化因子で修正された和(以下,ここでは修正された和と呼びます)の 大きさは,積分値からずれることを注意しておきます.この因子が正しい結果を導くことを次の節で確認しましょう.
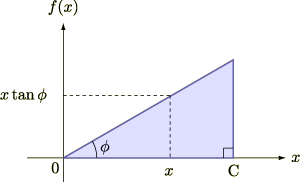
簡単な例(三角形の面積)
具体的な例として,一方の角の大きさが  で,底辺の長さが
で,底辺の長さが 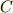 の直角三角形の面積を例に,
規格化因子が正しい結果を導く事を確認します.このとき関数
の直角三角形の面積を例に,
規格化因子が正しい結果を導く事を確認します.このとき関数 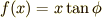 を閉区間
を閉区間 ![[0,C]](./78879b66de110fc12fc55c99df56ee51.png) の場合で考えれば良いです.
の場合で考えれば良いです.
簡単のために  は等差数列と考えると
は等差数列と考えると
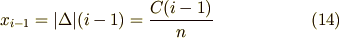
になります.分割の数が変わるのに対して,区間の方は決まっているので,分割の大きさ  が
が 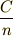 に
なります.
に
なります. 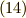 に
に  式を代入すると規格化因子は
式を代入すると規格化因子は
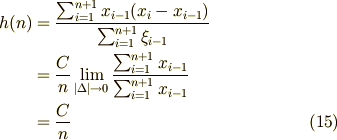
になります.そして次に 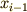 の和を計算すると
の和を計算すると
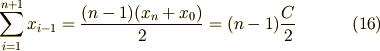
になります.すると  より三角形の面積
より三角形の面積  は次のようになるはずです(
は次のようになるはずです(  : 高さ).
: 高さ).
![S = \lim_{|\Delta| \to 0} \left[ h(n) \sum_{i=1}^{n+1} f(x_{i-1}) \right] &= \lim_{n \to \infty} \left[ \frac{C}{n} \tan \phi (n-1)\frac{C}{2} \right]\\ &= \frac{C^{2}\tan \phi}{2} \lim_{n \to \infty} \left( 1 - \frac{1}{n} \right) \\ &= \frac{CH}{2} \qquad[\because H = C \tan \phi] \tag{17}](./6ca48082756a8fc21435bb526491c990.png)
これは確かに三角形の面積の定義に一致します.ここで修正された和は極限をとらなければ積分値の 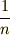 倍だけずれる
ことも分かります.前にも注意しておきましたが,これは規格化因子の定義の仕方が原因で起こっているのです.
最後,確認のために積分でも求めてみると結果は一致している事がわかります.
倍だけずれる
ことも分かります.前にも注意しておきましたが,これは規格化因子の定義の仕方が原因で起こっているのです.
最後,確認のために積分でも求めてみると結果は一致している事がわかります.
![\int_{0}^{C} x\tan \phi dx &= \tan \phi \left[ \frac{x^{2}}{2}\right]_{0}^{C} \\ &= \frac{C^{2}\tan \phi}{2} = \frac{CH}{2} \\ &= S \tag{18}](./6d8a20fad96cfa73ed793a9945a1d6bb.png)
和と積分との関係
規格化因子が正しい結果を出す事を確認したので,和との関係を見通しよくするために,積分の定義式を整理し直します.
三角形の面積を求める途中で分割の大きさを等しいと仮定しました.これでもなめらかな関数では十分に積分を定義することができます.
そのときの積分の区間を閉区間 ![[a,b]](./2c3d331bc98b44e71cb2aae9edadca7e.png) とすると,規格化因子は
とすると,規格化因子は 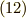 と
と 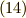 より
より

と書くことができます.このとき積分の定義式 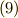 は次のように簡単化されます.
は次のように簡単化されます.
![\lim_{h \to 0} \left[ h \sum_{n=1}^{n+1}f(x_{i-1}) \right] = \int_{a}^{b} f(x) dx \tag{20}](./2c98d4b604508b3a4be6fdb7a4047f57.png)
つまりこのとき,積分とは和に極限を持たせるための因子  をかけたものの
をかけたものの 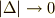 の極限と言えます.
これによって和と積分との間の隔たりが直感的にイメージしやすくなったと思います.
の極限と言えます.
これによって和と積分との間の隔たりが直感的にイメージしやすくなったと思います.
以上の説明から分かるように,和の極限が積分というのは短絡的な考えです.なぜならば規格化因子  が足りないからです.
この因子が無ければ,和には極限が存在しません.それはセクション3.に計算として示してあります.
が足りないからです.
この因子が無ければ,和には極限が存在しません.それはセクション3.に計算として示してあります.
注意
実は規格化因子などというもの,積分するときには考える必要はありません.また分割 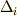 の大きさも揃える必要も無いのです.
積分の定義式
の大きさも揃える必要も無いのです.
積分の定義式 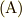 がむしろ和から積分への移行も容易ですし,厳密でもあります.
がむしろ和から積分への移行も容易ですし,厳密でもあります.
3.和が極限を持つための因子(おまけ)
おまけとして別の角度から規格化因子について考えていきます.ここでは和が極限を持つ事だけを考慮して因子の形を求めていき,
またその結果が積分の規格化因子と一致する事を確認します.
まず関数の和の性質を知るために,和  の
の 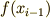 を
を  で,原点を中心に冪級数展開します.
で,原点を中心に冪級数展開します.
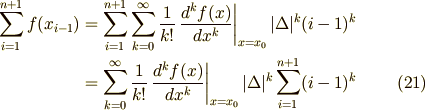
と書けます. 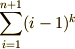 の最大の
の最大の 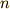 の冪数は
の冪数は 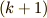 なので,
なので, 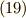 から
から  の冪数としては
の冪数としては 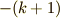 になります.
になります. 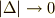 の極限では
消えてしまう
の極限では
消えてしまう ![{|\Delta|^{m} [m \ge 1]}](./7ab55d061d55735f8dccbe940433f228.png) の項を切り捨てて,冪数
の項を切り捨てて,冪数  の項の係数を
の項の係数を 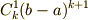 ,冪数
,冪数 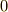 の項を
の項を 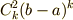 として
として 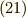 に代入すると
に代入すると
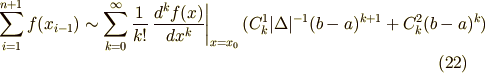
になります.するとこの式から 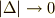 の極限は存在しない事が分かります(発散してしまいます).
ここで,できるだけ主要な項を引き出すにはどうしたら良いのか考えます.するとすぐに
の極限は存在しない事が分かります(発散してしまいます).
ここで,できるだけ主要な項を引き出すにはどうしたら良いのか考えます.するとすぐに 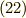 の両辺に
の両辺に  を
かければ良いことに気付きます.最後に
を
かければ良いことに気付きます.最後に 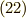 の両辺に規格化因子をかけて,極限をとることで次のように書けます.
の両辺に規格化因子をかけて,極限をとることで次のように書けます.
![\lim_{|\Delta| \to 0} \left[ |\Delta| \sum_{i=1}^{n+1} f(x_{i-1}) \right] &= \lim_{|\Delta| \to 0} \left[ \sum_{k=0}^{\infty} \frac{1}{k!} \left. \frac{d^{k}f(x)}{dx^{k}} \right|_{x=x_{0}} ( C_{k}^{1}(b-a)^{k+1} + C_{k}^{2}(b-a)^{k} |\Delta| ) \right] \\ \therefore \int_{a}^{b}f(x)dx &= \sum_{k=0}^{\infty} \frac{C_{k}^{1}}{k!} \left. \frac{d^{k}f(x)}{dx^{k}} \right|_{x=a} (b-a)^{k+1} \qquad [\because (20), x_{0} = a ]](./1d111951e19845c4ca58eecd595e5909.png)
もう少し整理すると次のように書けます.
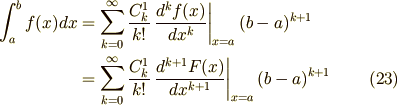
ここで 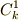 がどの値で上の等式を満足するかを示します.これは
がどの値で上の等式を満足するかを示します.これは  を
を
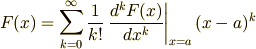
と 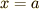 のまわりで冪級数展開したものから積分値を
のまわりで冪級数展開したものから積分値を
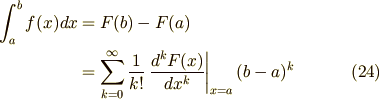
と書き,  と
と 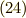 の
の 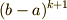 の係数それぞれを比較することによって完全に決まります.
の係数それぞれを比較することによって完全に決まります.