もう一度ベクトル2(ベクトルの読み書きそろばん)
0. 複数個のベクトルの取り扱いはどうするのか
ベクトルが1つしか出てこない場合よりも複数個出てくる状態の方がより一般的 ということには納得していただけるでしょうか? 例えば,物体に働く力を考える際,二つ以上の力が働かないと物体が釣り合うことは ありませんし,その力のかかっている角度しだいで運動する向きも変わってきます. 速度を考える際にも川を泳いで渡るときの状況を考えてみれば,実際の速度ベクトルは 「自分の泳いでいる速度ベクトル」と,「川の流れの分の速度ベクトル」との合成になり, "流されながら泳ぐ"という状況を考えなければいけません.
そういった複数個のベクトルの相互関係や相互作用をどう定量するかといった内容 がこのセクションでのテーマになります.
上記の内容についてはベクトルの和・差で表すことができます. 複数のベクトルの扱いには和・差の他にも定数倍,内積,外積という三つの積があり, 直感的には必要性を捉えづらいものの,和・差に加え三つの積を考えるといろいろな 数学的,物理的条件の取り扱いが便利になります.
ではベクトルの四則演算(にあたるもの)を考え,その「図形的な定義」と「代数的な表記」 をセクション毎に考えていきます.
以下,特に断らない限り,出てくるベクトルは全てゼロベクトル 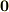 ではない
場合とします.
ではない
場合とします.
1. 和,差
先ず和ですね.図形的解釈から解説しましょう. ベクトルの和は
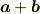
というように表記し,普通の数と同様に 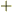 の記号を使って和を考えます.
図形的には
の記号を使って和を考えます.
図形的には  の終点に
の終点に 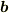 の始点を平行移動してきて重ね,
の始点を平行移動してきて重ね,
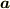 の始点から
の始点から 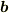 の終点をそれぞれ始点,終点となるようなベクトルを
の終点をそれぞれ始点,終点となるようなベクトルを
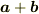 とします.
そうすると以下の図のようになり,平行四辺形が表れることになります.
ここで注意して見てもらいたいのはベクトルの和がどちらを先に和をとっても結果が
変わらないことです.
ここで「ベクトルを平行移動して一致すれば同じベクトルとみなす」ということが効いてきます.
とします.
そうすると以下の図のようになり,平行四辺形が表れることになります.
ここで注意して見てもらいたいのはベクトルの和がどちらを先に和をとっても結果が
変わらないことです.
ここで「ベクトルを平行移動して一致すれば同じベクトルとみなす」ということが効いてきます.
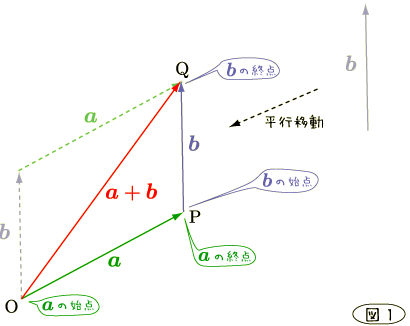
感覚的にわかりやすい例としては移動しているところを考えてみるとわかりやすいでしょう.
「点 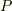 から点
から点  に2ステップ踏んでいったけど結局1ステップで行ったらどうなのよ?」
というのが
に2ステップ踏んでいったけど結局1ステップで行ったらどうなのよ?」
というのが 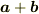 で表されるベクトルです
で表されるベクトルです
では代数的側面を見てみましょう.具代的に表記を与えると以下の式になります.
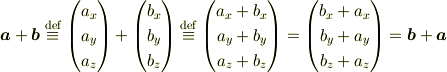
つまり成分ごと足してあげればいいんです.成分同士が可換(和の順序が交換可能) なのでベクトルの和も可換になります.
ここでvectorの原義で書いた”運搬”と言う原義に納得していただけるのではないでしょ うか. ゴールがどこかには興味があるが運んだ道筋には興味はないといった解釈でしょう. つまりその点に行く際に,和の順序を変えても(移動する順番を変えても)ベクトルの 和の結果(行き着く点)は変わらないということです.
次に差に触れます.
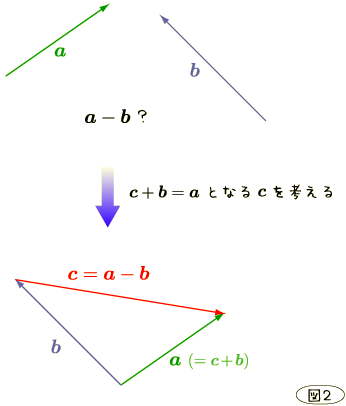
図形的側面の差は捉えづらいのでちょっと注意して図と文章を眺めてください.
ベクトルの差は  等と書き,普通の数と同様
等と書き,普通の数と同様  を用いて表します.
そしてその意味としては
を用いて表します.
そしてその意味としては  とは以下の図で
とは以下の図で 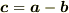 としたとき,移項して
としたとき,移項して  となる
となる  を考えてあげると
解決します.
ここで
を考えてあげると
解決します.
ここで  は
は 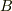 から
から 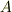 に向かうベクトルになっていることはちょっと注意です.
に向かうベクトルになっていることはちょっと注意です.
代数的な考え方の方の差は成分ごとの差に変わるだけなので比較的納得しやすい かと思います.具体的に表記すると
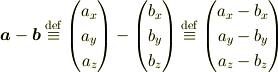
となります.
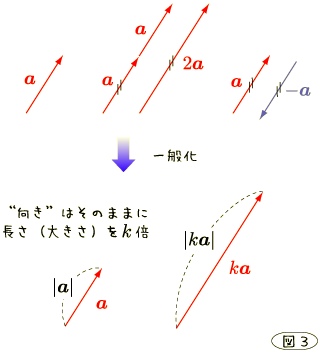
2. 定数倍
ベクトルは向きと大きさが同じベクトルを「同じベクトル」と見なすのでそのベクトル を表現する際に向きと大きさ両方が必要です. [*] ここでスポットが当たるのがその大きさになります.
ベクトルの定数倍が何を表すのかといえば,「向きは変化させずにその大きさのみを変化 させる」というのが定数倍で表現される内容です. ここで言っている"定数"というのはスカラー(普通の数)のことなので,「スカラー倍」なんて 言うこともあります.
具体的には文字式の積のように  を省いて文字同士をくっつけて
を省いて文字同士をくっつけて
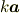
等と書きます( 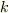 はその際の適当な定数)
はその際の適当な定数)
図形的側面を考えますと先ほど述べたとおり矢印を伸ばす度合いと考えます.
例えば 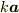 であれば
であれば 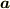 向きをそのままに
向きをそのままに 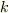 倍の長さに伸ばしたもの
と考えます.
倍の長さに伸ばしたもの
と考えます.
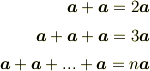
と考えると感覚的にもわかりやすいのではないでしょうか.
例えば 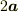 であれば
であれば 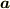 で移動したあと再び
で移動したあと再び 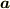 分移動した点へ
向かうベクトルと考えてあげるとちょうど
分移動した点へ
向かうベクトルと考えてあげるとちょうど 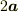 は
は 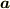 と平行で大きさだけ
2倍したものと考えられます.
上記の演算では当然整数倍しか作れませんが数学においてはお約束の"一般化"で定数倍
に拡張し,「向きはそのままに大きさだけ
と平行で大きさだけ
2倍したものと考えられます.
上記の演算では当然整数倍しか作れませんが数学においてはお約束の"一般化"で定数倍
に拡張し,「向きはそのままに大きさだけ 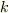 倍したベクトル」が
倍したベクトル」が 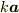 の定義
となります.
また,定数に
の定義
となります.
また,定数に  を採用したものを平行で逆に向かう同じ大きさの矢印とします.
そうすれば定数が負の場合は
を採用したものを平行で逆に向かう同じ大きさの矢印とします.
そうすれば定数が負の場合は 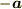 をまた定数倍すると考えてあげればいいからです.
例えば
をまた定数倍すると考えてあげればいいからです.
例えば 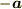 であれば
であれば
![&\bm{a}-\bm{a}\\=&\bm{a}+[-\bm{a}]\\=&\bm{0}](./9c7ddb3cab6bf4aebedb8e703c0f3087.png)
とゼロベクトルとなり,ベクトルの和の結果移動していない点に行くベクトルになり, 結局のところ,戻ってきてしまうという事実にも一致しています.
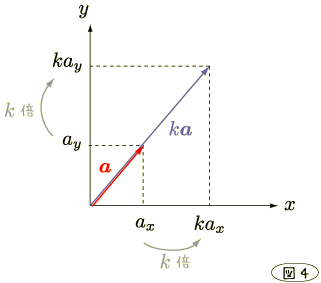
では代数的側面に移りましょう.具体的な表記では定数が各成分にかかります.二次元のデ カルト座標で考えると相似拡大(または縮小)されているところが視覚的に読み取れるかと思 います.

以上の内容から「 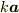 は
は 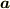 平行」という事実を注意しておきたいと思い
ます.言われてみれば当たり前ですが,純粋に数学的な問題で「〜という条件を満たす
ベクトルが
平行」という事実を注意しておきたいと思い
ます.言われてみれば当たり前ですが,純粋に数学的な問題で「〜という条件を満たす
ベクトルが 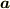 と平行であることを証明せよ」と言われたらそのベクトルの条件
が
と平行であることを証明せよ」と言われたらそのベクトルの条件
が 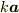 とかけることが目標になります.
とかけることが目標になります.
| [*] | 「 もう一度ベクトル1 」では「三次元の位置(ベクトル)を決めるには三つの量が必要」
と書いてあったのに,話が変わっているんじゃないかと思ったかもしれませんが,確かに
向きと大きさを決めれば平行移動も含めてベクトルは一通りに決まります.先ず大きさ
を固定してみるとそれはベクトルの始点を中心としてその大きさを半径とする球状を
終点が動きます.その中で,ある向きを持った直線と球の交点はというと…1つしかあり
ませんね!?自由度という概念を使って考えて見ますと,先ず大きさを決めた時点で,
ベクトルの各成分の自乗和が定数になることから自由度は3から1つへって2になります.
三次元の曲座標から明らかなように向きを指定することは 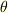 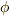 の2つの変数を指定するので自由度は2つ減って0.つまり,一意的に決まったことになります.
の2つの変数を指定するので自由度は2つ減って0.つまり,一意的に決まったことになります. |
単位ベクトル
数学でも物理でもよく単位ベクトルなる絶対値が 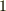 のベクトルをよく作ります.
なぜかというと単位ベクトルを作っておけば定数倍して簡単にいろんな大きさの
ベクトルが作れるからです.
例えば後述の外積による操作で得られたベクトルはその演算の中ですでに大きさが
決まってしまいます.その際,求めたいベクトルと向きは合っているけど大きさが
違う場合,一端単位ベクトルを計算し,大きさを規格化したあと欲しい大きさ倍
して求めたいベクトルを得るわけです.
のベクトルをよく作ります.
なぜかというと単位ベクトルを作っておけば定数倍して簡単にいろんな大きさの
ベクトルが作れるからです.
例えば後述の外積による操作で得られたベクトルはその演算の中ですでに大きさが
決まってしまいます.その際,求めたいベクトルと向きは合っているけど大きさが
違う場合,一端単位ベクトルを計算し,大きさを規格化したあと欲しい大きさ倍
して求めたいベクトルを得るわけです.
大きさが 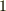 のベクトルを作るには自分の長さで割ってあげます.
したがって適当な
のベクトルを作るには自分の長さで割ってあげます.
したがって適当な 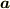 に平行な単位ベクトル
に平行な単位ベクトル 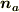 は
は
![\bm{n_\bm{a}}=&\frac{\bm{a}}{|\bm{a}|} \\=&\frac{1}{\sqrt[]{\mathstrut a_x^2+a_y^2+a_z^2}}\begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}](./8f43ffa9269169076807492199b4711e.png)
とかけます.つまり定数倍の 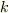 が
が ![\frac{1}{\sqrt[]{\mathstrut a_x^2+a_y^2+a_z^2}}](./88c732295969457d10d0385a0cd66ca2.png) となっているということです.
となっているということです.

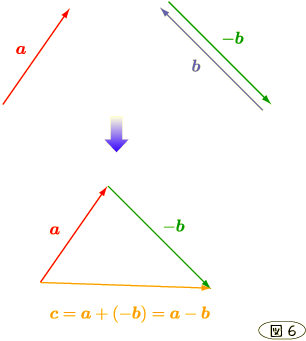
ベクトルの差
逆向きのベクトル,つまり負の定数倍のベクトルを定義したので今一度ベクトルの差を 考えて見ましょう.ベクトルの"差"を"負の足し算"と言い換えてあげれば
![\bm{a}-\bm{b}=\bm{a}+[-\bm{b}]](./c5a456146c176519d49d2afd3a39cb14.png)
と考えてあげれば以下の図で納得してもらえるはずです
3. 内積と外積
和と差に関する概念は理解できたでしょうか?では実数の四則演算での積の概念にあたるも のを解説します.本当のことを言うと商の概念は出てきません [†] ので,積についてだけ考えれば いい事になります.
そもそもベクトルとベクトルってどうやってかけるんでしょう?和と差は成分ごとに和と差を 取ればよかったので比較的納得しやすいんです. 問題は積です. 和・差の代数関係から直接拡張すると同じ成分を掛け合わせることを考えられますが 実際はそういうふうにはなっていなくてちょっと複雑です. そういう事情があり,積の代数的な定義に関しては注意深く定義を読まなければなりません.
内積
では先ず内積から.
内積は
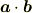
と書き,積という言葉通り掛け算の省略記号に当たる  を使って書きます.
ここで,「積だから」という理由で
を使って書きます.
ここで,「積だから」という理由で  は使わないでください.
こちらは外積を表すための記号で,数学では使い分けています.
は使わないでください.
こちらは外積を表すための記号で,数学では使い分けています.
図形的定義は次図になります.

つまり 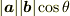 となるスカラーになります.(
となるスカラーになります.( 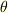 は
は 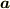 と
と 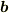 の始点をそろえたときに2つのベクトルの成す角)
この性質から内積をスカラー積と呼ぶこともあります.
図形的意味としては
の始点をそろえたときに2つのベクトルの成す角)
この性質から内積をスカラー積と呼ぶこともあります.
図形的意味としては 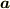 を
を 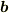 に射影させた辺の長さ
に射影させた辺の長さ
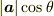 に
に 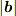 をかけた量です. [‡]
直接「ここの長さが内積の値」という量ではなく上記のような位置関係にある「2ベクトル間
で与えられる関数」と捉えると内積というのは『二つのベクトルがどれくらい似ているか』
を示す比と見ることが出来ます.
をかけた量です. [‡]
直接「ここの長さが内積の値」という量ではなく上記のような位置関係にある「2ベクトル間
で与えられる関数」と捉えると内積というのは『二つのベクトルがどれくらい似ているか』
を示す比と見ることが出来ます.
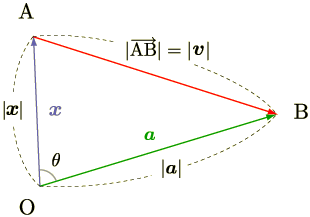
内積の代数的定義を表現すると
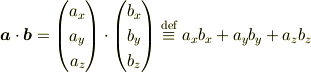
となります. 余弦定理に座標を代入すると導けるので挑戦してみましょう.(解答は最下段)
また代表的な関係を以下にあげると

外積
それでは外積に入ります.
外積は
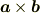
と書き,積という言葉通り掛け算の記号を使って  を使って書きます.
ここで,「積だから」という理由で
を使って書きます.
ここで,「積だから」という理由で  は使わないでください.
こちらは内積を表すための記号で,数学では使い分けます.
は使わないでください.
こちらは内積を表すための記号で,数学では使い分けます.
外積の図形的定義は次図のようになります.

つまり 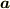 と
と 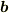 に共に垂直で大きさが
に共に垂直で大きさが
 となる
ベクトル量になります.そのせいもありこちらはスカラー積に対応してベクトル積と言います.
図を全く用いずに説明するなら「
となる
ベクトル量になります.そのせいもありこちらはスカラー積に対応してベクトル積と言います.
図を全く用いずに説明するなら「 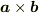 とは
とは 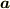 から
から
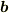 の順に回した
とき右ねじを回した際にねじが進む方向を向いている,大きさが
の順に回した
とき右ねじを回した際にねじが進む方向を向いている,大きさが
 のベクトル」ということになります.
また,ここで
のベクトル」ということになります.
また,ここで  は
は 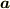 ,
, 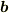 の2ベクトルで張られる
平行四辺形の面積になります.
の2ベクトルで張られる
平行四辺形の面積になります.
こちらは内積に対して『二つのベクトルがどれくらい違うか』を示す(ベクトル)量と見ることが 出来ます.
代数的な定義としては
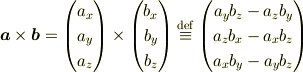
こちらも代表的な関係を挙げると
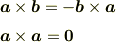
となります
| [†] | 実数の商はどのように考えられるかというと例えば 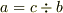 は は 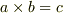 と
なる と
なる  を探すことにより得られます.これだけでは「必要条件だけではないか」と
言う意見も出るかもしれませんが,欲しい逆元が一意であれば得られた商は必要十分
条件を満たします.そんな理由があって を探すことにより得られます.これだけでは「必要条件だけではないか」と
言う意見も出るかもしれませんが,欲しい逆元が一意であれば得られた商は必要十分
条件を満たします.そんな理由があって  では割れません.なぜなら では割れません.なぜなら  の値
に関係なく不定or不能になってしまうからです.どちらにしても必要十分条件は
満たされないことが理由です.では他の分野にも目を向けてみますと.行列なども
行列が正則であれば逆行列が存在し適当な演算(下記の場合左乗)することにより逆元
として の値
に関係なく不定or不能になってしまうからです.どちらにしても必要十分条件は
満たされないことが理由です.では他の分野にも目を向けてみますと.行列なども
行列が正則であれば逆行列が存在し適当な演算(下記の場合左乗)することにより逆元
として 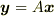 から から 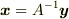 が得られます.つまり逆元
が一意である逆演算が定義できれば実数でいう"商"にあたるものが考えられないか
と考えたわけです.そこでベクトルの2積に関しても考えてみますと,内積
は2つのベクトルの成す角とその大きさがともに等しければ同じ値をとるので,
逆元は無数にあるので,逆演算は定義できそうにありません.では一方外積はどう
でしょう?図から考えるに,関係は一意ですから逆演算は考えられそうですが,なかなか
シンプルには表せそうもありません.書籍の中で見かけたこともないのですっきりとした
表記にはならないのかもしれません.また,実用性もあまりないのかもしれませんね.
そういえば差も和の逆演算として定義されます. が得られます.つまり逆元
が一意である逆演算が定義できれば実数でいう"商"にあたるものが考えられないか
と考えたわけです.そこでベクトルの2積に関しても考えてみますと,内積
は2つのベクトルの成す角とその大きさがともに等しければ同じ値をとるので,
逆元は無数にあるので,逆演算は定義できそうにありません.では一方外積はどう
でしょう?図から考えるに,関係は一意ですから逆演算は考えられそうですが,なかなか
シンプルには表せそうもありません.書籍の中で見かけたこともないのですっきりとした
表記にはならないのかもしれません.また,実用性もあまりないのかもしれませんね.
そういえば差も和の逆演算として定義されます. |
| [‡] | 射影という日本語からは直接導き出せないかもしれませんが射影した後の図形は射影の
対象となった図形(又は図形量)に如何に近いかといった事と非常に関連があります.
なぜなら,射影する元の図形の射影の対象となる図形成分(又はそれに相当するもの)を
表しているからです.内積で言えば 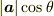 が射影された量で,
射影量に射影の対象となった が射影された量で,
射影量に射影の対象となった 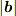 をかけていると考えるとより内積に関する
イメージも湧きやすくなるのではないでしょうか. をかけていると考えるとより内積に関する
イメージも湧きやすくなるのではないでしょうか. |
4. まとめ
これで一通りのベクトルの読み書きそろばんが終わりました.しかし,実数に関して
四則演算をマスターしたからといって二次方程式が解けないようにベクトルの実用上
は上記の内容だけでは全くの不足です.大工が大工道具の手入れを怠らないように,
料理人が包丁の手入れを怠らないように,僕たちも数学を道具として使う以上,常に
最良の状態にしておかねばなりません.また,内積と外積はその大きさが 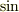
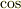 と
いう相補的な関係にあることは記憶にとどめるのに1つの助けになるかもしれません.
と
いう相補的な関係にあることは記憶にとどめるのに1つの助けになるかもしれません.
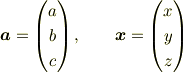
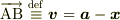 とすると,成分を用いて
とすると,成分を用いて
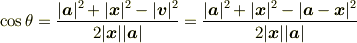
![\bm{x}\cdot\bm{a}=&|\bm{x}||\bm{a}|\cos{\theta} \\=&|\bm{x}||\bm{a}|\frac{|\bm{a}|^2+|\bm{x}|^2-|\bm{a}-\bm{x}|^2}{2|\bm{x}||\bm{a}|} \\=&\frac{1}{2}[|\bm{a}|^2+|\bm{x}|^2-|\bm{a}-\bm{x}|^2] \\=&\frac{1}{2}\{(x^2+y^2+z^2)+(a^2+b^2+c^2)-[(a-x)^2+(b-y)^2+(c-z)^2]\} \\=&\frac{1}{2}\cdot2(ax+by+cz) \\=&ax+by+cz](./bd0a3fa04e09323be0dea7fdd3e98230.png)