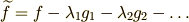ラグランジェの未定乗数法
ラグランジェの未定乗数法というのは,「拘束条件がある関数」の極値を求める数学的テクニックです. とても重要な計算テクニックなので,ここで紹介します. この節では,最初にいきなり計算の仕方を紹介します. 計算だけを読んでも覚えにくいと思いますので,最後に例題も載せます. 例題をやりながらまた最初の説明に戻る,ということを何度か繰り返してみてください. 幾つか問題を解いてみれば,便利さを体感して頂けると思います. 一回なんとなく理解しておけば,忘れてしまっても, また使うときに「物理のかぎしっぽ」のページで復習すれば良いだけです.
(※変数に付加的な条件式のことを,ここでは拘束条件と呼んでいます.)
計算のしかた(ひととおり)
まずは  ,
,  ,
,  の三変数の関数
の三変数の関数 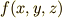 の極値を求める方法を考えます.
の極値を求める方法を考えます.
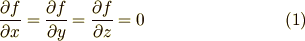
ここで  ,
,  ,
,  が互いに独立ならば話は簡単で,
偏導関数
が互いに独立ならば話は簡単で,
偏導関数 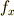 ,
, 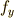 ,
, 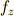 を連立して解けば良いだけですね.
(
を連立して解けば良いだけですね.
( 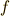 の右下に小さく
の右下に小さく  とか
とか  とか書いてあるのは,
とか書いてあるのは,
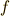 を
を  や
や  で偏微分したという略記号です.慣れておくと便利です.)
で偏微分したという略記号です.慣れておくと便利です.)
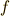 はもちろん微分可能な関数だとします.
はもちろん微分可能な関数だとします.
難しいのは,なんらかの拘束条件がある場合です.
拘束条件があると,  ,
,  ,
,  は互いに独立ではないので,
それぞれ勝手に偏微分することが出来ないからです.
拘束条件は
は互いに独立ではないので,
それぞれ勝手に偏微分することが出来ないからです.
拘束条件は  ,
,  ,
,  の関数ですから,一般に式(2)のように表せます.
の関数ですから,一般に式(2)のように表せます.

(2)式がある一つの変数に対して陽に解けてしまうことがあるかも知れません.
それならば(1)式と(2)式を連立して,変数を一つ消せばいいだけなので簡単です.
これから考えるのは特に(2)式が陽に解けないような場合です.
(※陽に解くというのは, 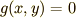 のような形をしていた関数
を式変形して
のような形をしていた関数
を式変形して 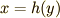 のような形にすることです.)
のような形にすることです.)
関数 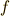 ,
, 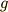 は極値近傍で次の式を満たすと考えられます.
は極値近傍で次の式を満たすと考えられます.
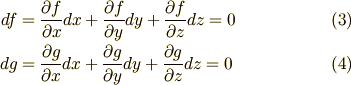
(3)式と(4)式は見かけは同じですが,違うのは関数の名前だけではありません.
本質的に式の意味することが異なることをここで理解しておくのが大事です.
普通の日本語に直すと,(3)式が意味するのは「関数 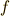 が極値を取る」ということです.
一方,(4)式が意味するのは「拘束条件
が極値を取る」ということです.
一方,(4)式が意味するのは「拘束条件 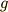 が
あるので,
が
あるので,  ,
,  ,
,  は互いに勝手には動けない」ということなのです.
だから
は互いに勝手には動けない」ということなのです.
だから 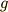 は極値近傍でなくても(4)式を満たしますね.よく頭の中を整理しながら読んで下さい.
は極値近傍でなくても(4)式を満たしますね.よく頭の中を整理しながら読んで下さい.
ここで,式(3),(4)から形式的に 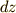 を消すような連立をしましょう.
を消すような連立をしましょう.
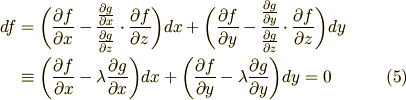

(5)式はすでに条件式(2)を中に含んでいるので,外部にはもう拘束条件がありません.
つまり,(5)式の  と
と  は独立変数になっているということです.
こうなればしめたものです.
は独立変数になっているということです.
こうなればしめたものです.  と
と 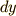 がそれぞれ勝手に動けるのですから,
「右辺
がそれぞれ勝手に動けるのですから,
「右辺 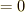 」が成り立つならば,中辺に含まれる括弧は
それぞれ恒等的に零になっている,と考えることができますね.
」が成り立つならば,中辺に含まれる括弧は
それぞれ恒等的に零になっている,と考えることができますね.
(5) ⇔


また(6)式は次のように書き換えられます.
(6) ⇔

ここで 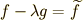 と置けば,式(7)(8)(9)は次の三式に帰着しますね.
(
と置けば,式(7)(8)(9)は次の三式に帰着しますね.
( 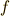 の上に〜がついていますが,これはエフ・チルダと読みます.)
の上に〜がついていますが,これはエフ・チルダと読みます.)
(7)(8)(9) ⇔
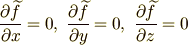
これは関数 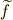 に関する極値問題です.
しかもここで,
に関する極値問題です.
しかもここで,  ,
,  ,
,  には何も拘束条件が課せられていませんから,
普通にそれぞれ
には何も拘束条件が課せられていませんから,
普通にそれぞれ 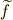 の導関数を連立して解けば良いだけです.
なんだか魔法のように拘束条件が見えなくなってしまいました.
これがラグランジェの未定乗数法というテクニックです.
の導関数を連立して解けば良いだけです.
なんだか魔法のように拘束条件が見えなくなってしまいました.
これがラグランジェの未定乗数法というテクニックです.
まとめ
今までやったことを一言で書くと『拘束条件 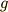 のある関数
のある関数 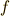 の極値問題は,
拘束条件の無い
の極値問題は,
拘束条件の無い  の極値問題に変換できる』と言うことです.
ただし,未知数が
の極値問題に変換できる』と言うことです.
ただし,未知数が  ,
,  ,
,  ,
,  の4つに増えていることに注意です.
普通は,変数や式の数は少ない方が計算が楽ですから,なるべく変数や式を減らすことを考えます.
しかし,自由に微分の計算が出来ないことはもっと不便ですから,
反対にわざと変数の数を増やして,その代わり自由に微分が出来るようにしたのです.
今までの計算で何をやっていたのかというと,そういうことだったのです.
の4つに増えていることに注意です.
普通は,変数や式の数は少ない方が計算が楽ですから,なるべく変数や式を減らすことを考えます.
しかし,自由に微分の計算が出来ないことはもっと不便ですから,
反対にわざと変数の数を増やして,その代わり自由に微分が出来るようにしたのです.
今までの計算で何をやっていたのかというと,そういうことだったのです.
補足
ここでは  の物理的意味は曖昧で,単に数学的なテクニック
として登場した変数のように見えるますが,実際の物理の問題において
は
の物理的意味は曖昧で,単に数学的なテクニック
として登場した変数のように見えるますが,実際の物理の問題において
は  が重要な意味を持つ物理量になっていることが少なくありません.
が重要な意味を持つ物理量になっていることが少なくありません.
注意
ラグランジェの未定乗数法が使えない場合があります.
それは,極値を与える 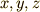 の組に対して
の組に対して 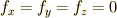 となってしまう場合です.
このとき,式(7)(8)(9)を連立しても
となってしまう場合です.
このとき,式(7)(8)(9)を連立しても  を決めることが出来ません.
を決めることが出来ません.
例題
例題1.[楕円に内接する四角形の面積]
『長径2a,短径2bの楕円に内接する長方形の面積の最大値を求めよ.』
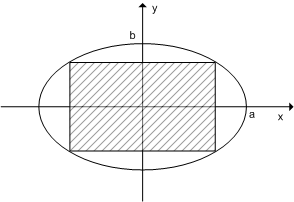
解答
四角形の面積を  ,楕円に内接するという拘束条件を
,楕円に内接するという拘束条件を 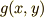 とおきます.
とおきます.

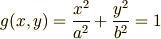
未定乗数  を導入して,
を導入して, 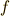 から
から 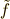 に変数変換します.
に変数変換します.
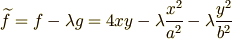
このとき,次の三式を  ,
,  ,
,  を独立変数のよう
に見なして連立すればよいだけです.式が3本,変数が3つですから,問題なく解けますね.
を独立変数のよう
に見なして連立すればよいだけです.式が3本,変数が3つですから,問題なく解けますね.

これより次の結果を得ます.
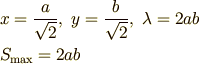
はい,これで楕円に内接する四角形の最大値が出ました. !(^^)!
でも,ちょっと待てよ,と思った読者の方はいませんか? 実は,ここで求めたのは,楕円に内接する四角形の「極値」に過ぎません. 単に極値と言えば,極小値や変曲点も含まれますので, 数学的にはこの計算からだけでは「最大値」を求めたとは言えないのです. しかし,楕円に内接する四角形の面積が極値を持つとすれば, それは直感的に最大値だけです.一般に関数の二次導関数まで調べたりするのは大変なことですから, 物理学では直感的に明らかな問題に対しては,一次導関数を調べただけで, 最大だ,最小だ,と決めてしまうことがよくあるのです. 物理学の計算では「直感的に当たり前のことは手間を省く」ということがとても大事なことです. 直感的に明らかで無い問題の場合には,きちんと二次導関数も調べて,最大・最小を確認します.
例題.2
『二つの実数  ,
,  が
が 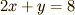 を満たすとき,
を満たすとき, 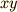 の最大値を求めなさい.』
の最大値を求めなさい.』
解答

とおきます.このとき 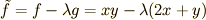 と置いて
次の計算をすればいいというのは,もう大丈夫ですね.
と置いて
次の計算をすればいいというのは,もう大丈夫ですね.

式(2),(3),(4)を連立すると, 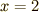 ,
, 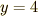 ,
, 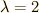 という結果を得ます.
という結果を得ます.
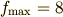
はい,これで最大値が出ました. !(^^)!
……答は合ってるんですけど,実は,これは少しひっかけ問題で, 何もラグランジェの未定乗数法を使わなくても 次のように二次方程式の平方完成で簡単に解けてしまうのでした. 実は高校生の数Iから拾ってきた問題だったのです.
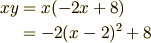
最大値は 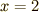 の時, 8 になることがわかります.
の時, 8 になることがわかります.
大学生の人へ
ラグランジェの未定乗数法を使うと,大抵の条件付最大最小問題は解けるようになってしまいます. しかし,慣れてくると,逆に簡単な方法を忘れてしまったりするので要注意です.
高校生・受験生の人へ
最大・最小問題の解き方には相加相乗平均を使うとか色々なテクニックがあって, 難しいと思います.ラグランジェの未定乗数法で大抵の問題は解けてしまいますから, 難しいのがあったら,こっそり使って検算しましょう.