逆行列のよく使う性質
逆行列を掛けるということは, どういうことなのか. 一つの解釈を書きたいとおもいます.
基本的性質
行列はベクトルを並べたものとして考えると, 分かり易いです.
例えば,
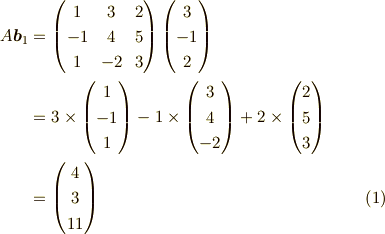
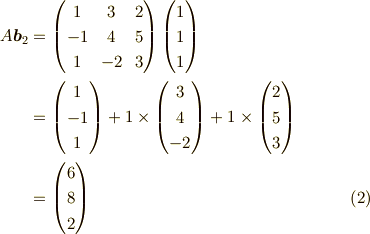
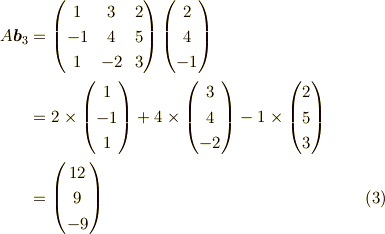
という風に,行列と列ベクトルの積は,
行列 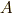 を列ベクトル
を列ベクトル 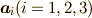 に分解し,
右から掛ける列ベクトル
に分解し,
右から掛ける列ベクトル 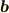 の成分をその係数にして
掛け合わせたものとなります.
の成分をその係数にして
掛け合わせたものとなります.
この三つの列ベクトルを並べて行列を作りますと,
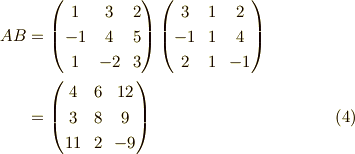
逆行列
ここで,有限次元の行列 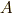 を構成する列ベクトル
を構成する列ベクトル 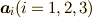 を並べたものとして,
更に,
を並べたものとして,
更に, 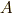 が逆行列を持つ(正則である)と考えてみましょう [*] .
が逆行列を持つ(正則である)と考えてみましょう [*] . 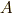 の逆行列を
の逆行列を 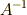 と置きます.
と置きます.
| [*] | 行列は行基本変形や列基本変形で標準形を求めたとき, 階数が行列の次元に等しいと正則といい, 逆行列をもつのでした. |
すると,逆行列の定義から,
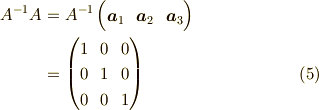
つまり,これを分解すると,
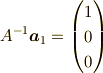
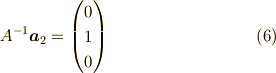
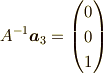
と成ります.
重ね合わせの原理
行列と列ベクトルは線形性を持ちます.
つまり,行列 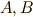 とし,列ベクトル
とし,列ベクトル 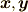 は,
は,
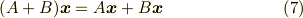
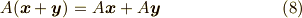
が成り立ちます.
よって,式 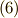 の第一式に係数
の第一式に係数 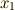 を掛け,
第二式に
を掛け,
第二式に 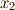 を掛け,第三式に
を掛け,第三式に 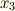 を掛け
足し合わせたものを作ると,
を掛け
足し合わせたものを作ると,
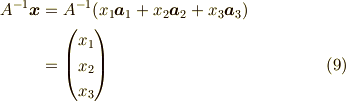
と成ります.つまり,逆行列 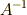 は,列ベクトル
は,列ベクトル 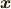 を,列ベクトル
を,列ベクトル 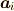 の線形結合
の線形結合

として表した
時の, 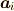 の係数を列ベクトルとして
取り出す操作であることが分かります.
の係数を列ベクトルとして
取り出す操作であることが分かります.
これで,列ベクトル 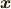 の代わりに,
行列
の代わりに,
行列 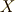 に作用させた時を考えると,
に作用させた時を考えると,
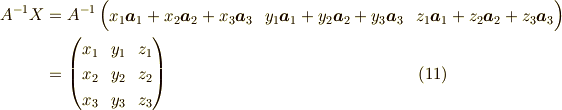
となる訳です.
その他応用例
ここで簡単な応用例を書きます. 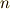 次元正方行列
次元正方行列 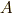 の固有ベクトルが,次元の数
の固有ベクトルが,次元の数 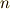 個あるとき,
固有値を
個あるとき,
固有値を 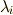 ,固有ベクトルを
,固有ベクトルを 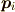 とします.
固有ベクトルを並べた
とします.
固有ベクトルを並べた 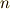 次の行列を
次の行列を 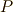 とします.
ここで,
とします.
ここで, 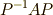 という行列を考えると,
という行列を考えると,
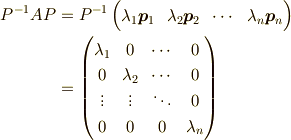
となり,対角化されることが分かりますね.
それでは,今日はこの辺で.