フーリエ級数1
周期関数を三角関数の足し合わせで表すものを,フーリエ級数
(級数とは数列の和.単に級数といった場合,無限級数を表すことが多い.フーリエ級数も無限級数)といいます.
三角関数とは 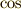 関数や
関数や 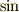 関数のことです.
これらは周期
関数のことです.
これらは周期 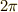 の周期関数で,下図のような形をしています.
の周期関数で,下図のような形をしています.
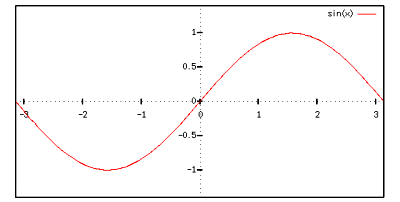 sin関数
sin関数
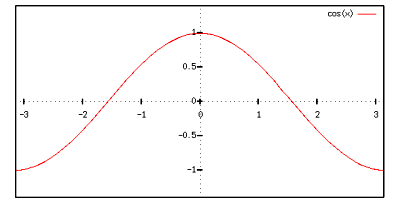 cos関数
cos関数
これは高校の数学で習いますね.
フーリエ級数でできること
この一見単純な関数を足し合わせる(重ね合わせる)ことで,周期関数であればどんな形の関数でも表せる, というのがフーリエ級数です.本当でしょうか.
足し合わせてみる
フーリエ級数をちょっと試してみましょう.つくりたい周期関数は
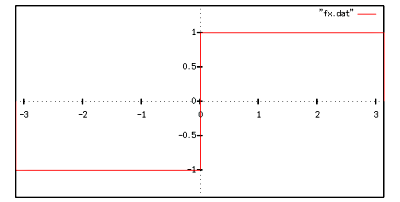
というものです.周期は 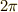 です.これは式で表すと
です.これは式で表すと
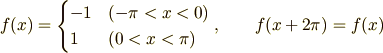
となります.この式と周期を元にどういうふうに三角関数を足せばいいか (すなわちフーリエ級数)がわかるのですが,その計算はまた後ほど.とりあえずフーリエ級数は
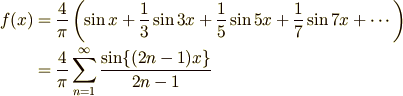
であると分かったものとします.これをグラフにしていきましょう.
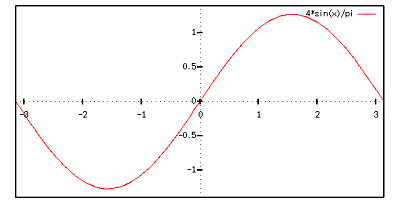
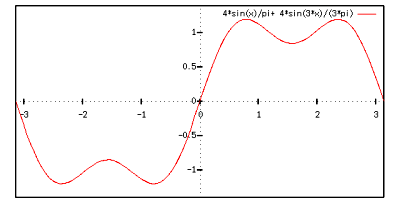
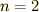
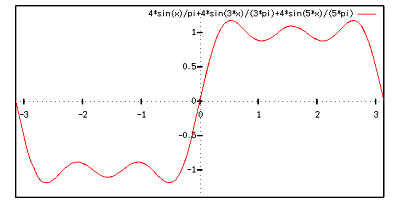
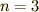
ここで 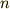 とは,足し合わせる三角関数の数です.
うーん,近づいてはいますがまだまだ足さないといけないようです.
gnuplotで直接グラフを書くのはしんどいので,つぎのCプログラムを使います.
とは,足し合わせる三角関数の数です.
うーん,近づいてはいますがまだまだ足さないといけないようです.
gnuplotで直接グラフを書くのはしんどいので,つぎのCプログラムを使います.
#include <stdio.h>
#include <math.h>
#define N 10 /* この値を変更 */
double term(int n, double x){
return sin((2*n-1)*x)/(2*n-1);
}
int main(void){
int i;
double x, y=0;
FILE *fp;
fp = fopen("fourier.dat", "w");
for (x=-M_PI; x<M_PI; x+=0.001) {
for (i=1; i<=N; i++) {
y += term(i,x);
}
fprintf(fp, "%lf %lf\n", x, 4/M_PI*y);
y=0;
}
fclose(fp);
return 0;
}
いま問題にしている関数のフーリエ級数を数値計算し,できたデータをプロットします.
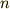 の値(プログラム中では定数 N )を変えながら,いくつか計算してみました.
の値(プログラム中では定数 N )を変えながら,いくつか計算してみました.
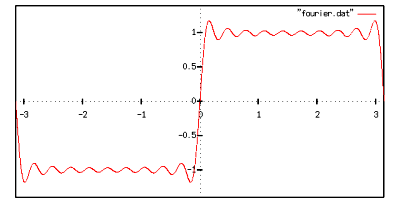
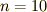
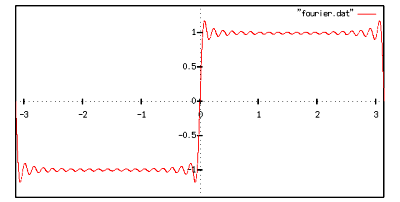
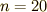
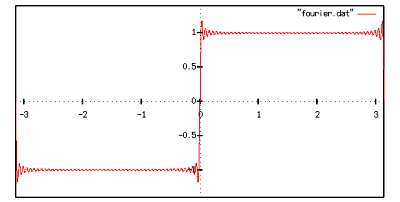
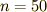
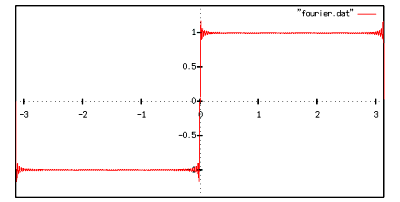
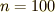
だいぶそれらしくなってきました.もっと足します.
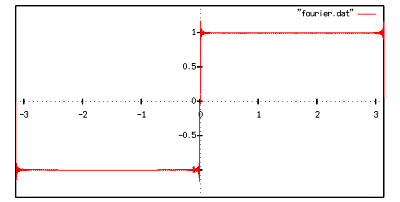
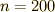
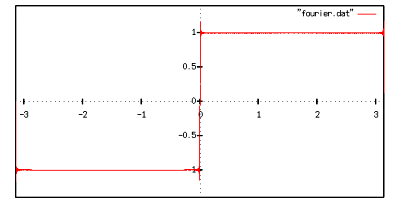
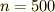
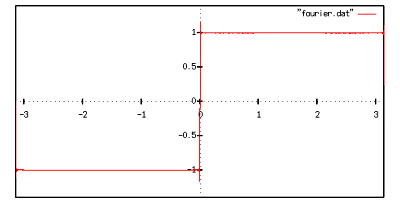
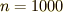
 の部分でうまく収束しません.これはギブスの現象と呼ばれます.
最後に,十万番目の項まで足したものを.
の部分でうまく収束しません.これはギブスの現象と呼ばれます.
最後に,十万番目の項まで足したものを.
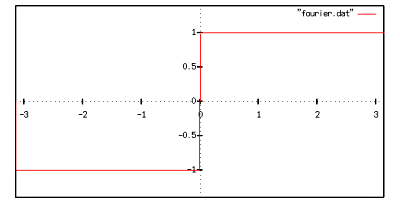
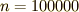
ほぼ完璧に見えますが,実際にはやはり  の部分がうまく収束していないハズです.
一般に有限個のフーリエ級数の和では完璧に周期関数を再現することはできません.
しかしたくさん足し合わせれば,完璧に近くなります.
(ちなみにこの計算には Pentium III 750MHz で2分くらいかかりました).
というわけで,周期関数は三角関数の足し合わせで再現できそうだということが分かりました.
の部分がうまく収束していないハズです.
一般に有限個のフーリエ級数の和では完璧に周期関数を再現することはできません.
しかしたくさん足し合わせれば,完璧に近くなります.
(ちなみにこの計算には Pentium III 750MHz で2分くらいかかりました).
というわけで,周期関数は三角関数の足し合わせで再現できそうだということが分かりました.