超関数入門
超関数の計算方法を簡単に例示してみることにします.
超関数の計算で基本になるのは,次のようなスカラー積(汎関数)
です. 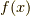 が超関数,
が超関数,  が試料関数と呼ばれるものです.
が試料関数と呼ばれるものです.
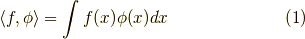
おおざっぱに言って,この  は
は  が十分大きいところで,
十分速く減衰しゼロになることを要求します.それを試料関数空間といいます.
そうすると,無限遠でゼロにならない超関数
が十分大きいところで,
十分速く減衰しゼロになることを要求します.それを試料関数空間といいます.
そうすると,無限遠でゼロにならない超関数 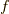 でも,スカラー積が有限値で
定まります.
でも,スカラー積が有限値で
定まります. 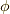 が試料関数空間でいろいろ動いた
とき,常に
が試料関数空間でいろいろ動いた
とき,常に 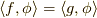 を満たしてるならば,
超関数の意味で
を満たしてるならば,
超関数の意味で 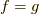 と同一視するのです.
と同一視するのです.
超関数の微分
そういっても,何が嬉しいのかわからないと思うので,簡単な例を示します.
階段関数 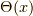 の微分を求めてみます.
これは,
の微分を求めてみます.
これは, 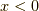 では0,
では0, 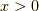 では1をとる関数です.
では1をとる関数です.  の値は定義されていません.
まず,準備として,関数の微分を求めておきます.
の値は定義されていません.
まず,準備として,関数の微分を求めておきます.
![\langle \dfrac{d}{dx}f ,\phi \rangle &= \int_{-\infty}^{\infty} \dfrac{df}{dx}(x) \phi(x) dx \\&= \left[ f(x) \phi(x) \right]_{-\infty}^{\infty} - \int_{-\infty}^{\infty} f(x) \dfrac{d \phi}{dx}(x) dx \\&= - \langle f ,\dfrac{d \phi}{dx} \rangle \tag{2}](./ef3c9d8e0ee632a17e4ae9674b43d235.png)
試料関数が無限遠で十分速く小さくなるので,境界項 ![\left[ f(x) \phi(x) \right]_{-\infty}^{\infty}](./b735eb4542c589dfa3c70ca4f24beb1f.png) はゼロとなる事を,
用いました.微分が移ると,マイナスの符号がつくことにご注意ください.では,階段関数の微分に入ります.
はゼロとなる事を,
用いました.微分が移ると,マイナスの符号がつくことにご注意ください.では,階段関数の微分に入ります.
![\langle \dfrac{d \Theta}{dx} ,\phi \rangle &= - \langle \Theta ,\dfrac{d \phi}{dx} \rangle \\&= - \int_{-\infty}^{\infty} \Theta \dfrac{d \phi}{dx} dx \\&= - \int_0^{\infty} \dfrac{d \phi}{dx} dx \\&= - \left[ \phi \right]_0^\infty \\&= - \left( \phi(\infty) - \phi(0) \right) \\&= \phi(0) \\&= \langle \delta(x) , \phi \rangle \tag{3}](./9b03408f8a87b168ba2ac1550c3bb740.png)
ここで,δ関数が出てきました.つまり,  が超関数の意味で成立します.
が超関数の意味で成立します.
超関数のフーリエ変換
超関数の考え方では,フーリエ変換
![\hat{f}(k) &= \mathcal{F}[f(x)] = \int f(x) e^{-ikx} dx \tag{4} \\f(x) &= \mathcal{F}^{-1}[\hat{f}(x)] = \dfrac{1}{2 \pi} \int \hat{f}(k) e^{ikx} dk \tag{5}](./04a075848dfb55ccf5cc16b61e5e708d.png)
を拡張することもできます.
例えば, 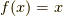 のフーリエ変換はいくつとなるでしょう?
これは従来のフーリエ変換では,積分が発散してうまく求まりません.
ところが,超関数の意味では求めることができるのです.
超関数のフーリエ変換の定義は,次のようになります.
のフーリエ変換はいくつとなるでしょう?
これは従来のフーリエ変換では,積分が発散してうまく求まりません.
ところが,超関数の意味では求めることができるのです.
超関数のフーリエ変換の定義は,次のようになります.
![\langle \mathcal{F}[f(x)] , \phi(k) \rangle &= \int_{-\infty}^\infty \left( \int_{-\infty}^\infty f(x) e^{-ikx} dx \right) \phi(k) dk \\&= \int_{-\infty}^\infty \left( \int_{-\infty}^\infty \phi(k) e^{-ikx} dk \right) f(x) dx \\&= \langle f(x) , \mathcal{F}[\phi(k)] \rangle \tag{6}](./c131c9846978051b62121678464fa3f9.png)
まず, 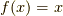 のフーリエ変換の前にいくらかフーリエ変換の例を考えてみましょう.
のフーリエ変換の前にいくらかフーリエ変換の例を考えてみましょう.
![\langle \mathcal{F}^{-1}[\delta(k)] , \phi(x) \rangle &= \dfrac{1}{2 \pi } \int \left( \int \delta(k) e^{ikx} dk \right) \phi(x) dx \\&= \dfrac{1}{2 \pi } \int 1 \times \phi(x) dx \\&= \langle \dfrac{1}{2 \pi } , \phi(x) \rangle \tag{7}](./6561bee4711845161fe89c14ccbac81a.png)
よって,
![\mathcal{F}^{-1}[\delta(k)] = \dfrac{1}{2 \pi } \tag{8} \\\mathcal{F}^{-1}[2 \pi \delta(k)] = 1 \tag{9}](./1cb828def810880f0c5ce5c8513f835d.png)
が言えました. これと,公式
![\mathcal{F} \mathcal{F}^{-1} [f(k)] = f(k) \tag{10}](./fdcbc0f0b4720a3d7134935bba0918b7.png)
を用いると,
![\mathcal{F}[1] = \mathcal{F} \mathcal{F}^{-1}[2 \pi \delta(k)] = 2 \pi \delta(k) \tag{11}](./c6a4d16801e2d37731a95b56954015c6.png)
が分かります.
では,いよいよ 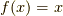 のフーリエ変換です.後で具体的計算を書きますので,
俯瞰図としてご覧ください.
のフーリエ変換です.後で具体的計算を書きますので,
俯瞰図としてご覧ください.
![\langle \mathcal{F}[x] , \phi(k) \rangle &= \langle x, \mathcal{F} [ \phi(k) ] \rangle \\&= -i \langle 1 , \mathcal{F} \left( \dfrac{d \phi}{dk} \right) \rangle \\&= -i \langle \mathcal{F}[1] , \dfrac{d \phi}{dk} \rangle \\&= -i \langle 2 \pi \delta(k) , \dfrac{d \phi}{dk} \rangle \\&= 2 \pi i \langle \dfrac{d \delta(k)}{dk} , \phi(k) \rangle \tag{12}](./c7a39676cb4262b3815cf16ad4f6cf47.png)
よって,
![\mathcal{F}[x] = 2 \pi i \dfrac{d \delta(k)}{dk} \tag{13}](./bbc5b7a14d9dc51d8b876584b129930d.png)
が分かりました.詳しい計算を書きますと,式 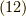 は,
は,
![\int \left( \int x e^{-ikx} dx \right) \phi(k) dk &= \int x \left( \int \phi(k) e^{-ikx} dk \right) dx \\&= \int x \left( [ \phi(k) \dfrac{e^{-ikx}}{-ix} ] + \int \dfrac{d \phi(k)}{dk} \dfrac{e^{-ikx}}{ix} dk \right) dx \\&= \dfrac{1}{i}\int \left( \dfrac{d \phi(k)}{dk} e^{-ikx} dk \right) dx \\&= -i \int \dfrac{d \phi}{dk} \left( \int e^{-ikx} dx \right) dk \\&= -i \int \dfrac{d \phi}{dk} 2 \pi \delta(k) dk \\&= -2 \pi i \int \dfrac{d \phi}{dk} \delta(k) dk \\&= -2 \pi i \left( \left[ \phi \delta(k) \right] - \int \phi \dfrac{d \delta(k)}{dk} dk \right) \\&= 2 \pi i \int \phi \dfrac{d \delta(k)}{dk} dk \tag{14}](./f4de0271f7bc22f16cb3f2d4b2e2db44.png)
これで,証明完了です.同様に,
![\mathcal{F}[x^n] &= 2 \pi i^n \dfrac{d^n \delta(k)}{dk^n} \tag{15} \\\mathcal{F}[\dfrac{d^n \delta(x)}{dx^n}] &= (ik)^{n} \tag{16}](./81bd234714996865e7cb16bff9b99de2.png)
が成立します.それでは,今日はこの辺で. お疲れ様でした.