∫1/√(x^2+a^2)dxの計算

この記事では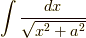， \int \dfrac{dx}{\sqrt{x^2+a^2}} を求めます．

本（下に紹介しておきます）を読んでいたら，この積分は 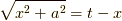\sqrt{x^2+a^2}=t-x と変数変換をすると書いてありました．どうやったらそんな置き方を考え付くの？と悩んでいたのですが，ふと，

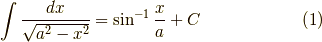
\int\dfrac{dx}{\sqrt{a^2-x^2}}=\sin^{-1}\dfrac{x}{a}+C \tag{1}

を，虚数単位を用いて 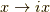x \to ix と置き換えたらいいのではないか？と思いました．そしたら，右辺は 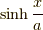\sinh\dfrac{x}{a} になるかな？と思ったら，どんぴしゃり！そうなるようです．さて，今示したいのは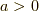， a>0 として，

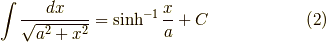
\int\dfrac{dx}{\sqrt{a^2+x^2}}=\sinh^{-1}\dfrac{x}{a}+C \tag{2}

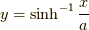です．右辺を y=\sinh^{-1}\dfrac{x}{a} と置き，微分すれば，左辺の被成分関数となることを確認すればよいでしょう．やってみると，

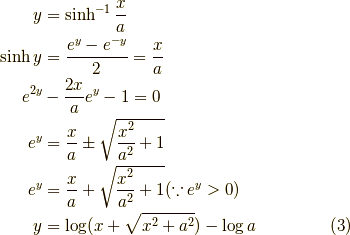
y&=\sinh^{-1}\dfrac{x}{a} \\\sinh y &= \dfrac{e^y - e^{-y}}{2} = \dfrac{x}{a} \\e^{2y} &- \dfrac{2x}{a}e^y -1 = 0 \\e^y &= \dfrac{x}{a} \pm \sqrt{\dfrac{x^2}{a^2}+1} \\e^y &= \dfrac{x}{a} + \sqrt{\dfrac{x^2}{a^2}+1} (\because e^y > 0 ) \\y&= \log (x + \sqrt{x^2+a^2})-\log a \tag{3}

であり，なんと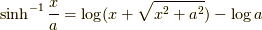， \sinh^{-1}\dfrac{x}{a} = \log (x + \sqrt{x^2+a^2})-\log a であることが分かりました．しかも，この式の右辺の 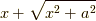x + \sqrt{x^2+a^2} は，本で天下り的に示されていた 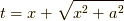t=x + \sqrt{x^2+a^2} ですね．やっと，結びつきました．更に進むと，

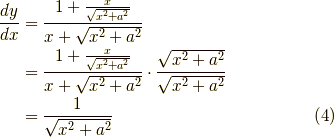
\dfrac{dy}{dx} &= \dfrac{1 + \frac{x}{\sqrt{x^2+a^2}}}{x + \sqrt{x^2+a^2}} \\&= \dfrac{1 + \frac{x}{\sqrt{x^2+a^2}}}{x + \sqrt{x^2+a^2}} \cdot \dfrac{\sqrt{x^2+a^2}}{\sqrt{x^2+a^2}} \\&= \dfrac{1}{\sqrt{x^2+a^2}} \tag{4}

となりました．確かに 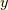y の微分が被積分関数になっていますね．

まとめ

覚えやすいように，他の積分と比較できるようにまとめておきます．いきなり書きますが，良い練習問題になると思います．まずは，右辺を 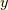y に等しいと置いて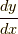， \dfrac{dy}{dx} を求めるのです．ちなみに 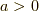a>0 としておきます．

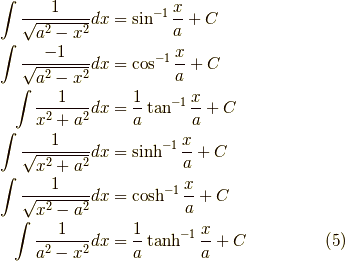
\int \dfrac{1}{\sqrt{a^2-x^2}}dx &= \sin^{-1} \dfrac{x}{a} +C \\\int \dfrac{-1}{\sqrt{a^2-x^2}}dx &= \cos^{-1} \dfrac{x}{a} +C \\\int \dfrac{1}{x^2+a^2}dx &=\dfrac{1}{a} \tan^{-1} \dfrac{x}{a} +C \\\int \dfrac{1}{\sqrt{x^2+a^2}}dx &= \sinh^{-1} \dfrac{x}{a} +C \\\int \dfrac{1}{\sqrt{x^2-a^2}}dx &= \cosh^{-1} \dfrac{x}{a} +C \\\int \dfrac{1}{a^2-x^2}dx &= \dfrac{1}{a}\tanh^{-1} \dfrac{x}{a} +C \tag{5}

これを求める際，得られた等式は以下の様になります．双曲関数は簡単ですが，三角関数は複素関数の知識がないとできないようです．

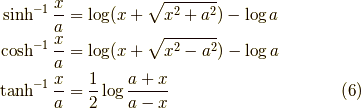
\sinh^{-1} \dfrac{x}{a} &= \log(x+\sqrt{x^2+a^2}) - \log a \\\cosh^{-1} \dfrac{x}{a} &= \log(x+\sqrt{x^2-a^2}) - \log a \\\tanh^{-1} \dfrac{x}{a} &= \dfrac{1}{2} \log \dfrac{a+x}{a-x} \tag{6}

それでは今日はこの辺で，お疲れ様でした．