畳み込み積分の微分
この記事では,
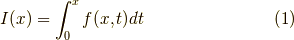
の微分,
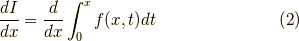
を求めた後,畳み込み積分の微分,
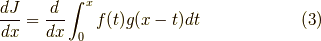
を求めます.
証明1:微分の定義に従う
まずは微分の定義に従ってこの 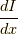 を求めてみましょう.
を求めてみましょう.
まずは復習です. 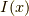 の微分の定義は,
の微分の定義は, 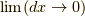 の時,
の時,
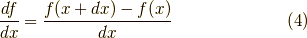
でしたね.よって, 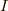 の微分は,
の微分は, 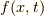 の
の 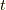 に関する原始関数を
に関する原始関数を 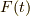 とおくと(つまり,
とおくと(つまり, 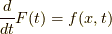 であり,ここで
であり,ここで  とおけば,
とおけば,  となります.),適宜
となります.),適宜 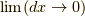 ととれば,
ととれば,
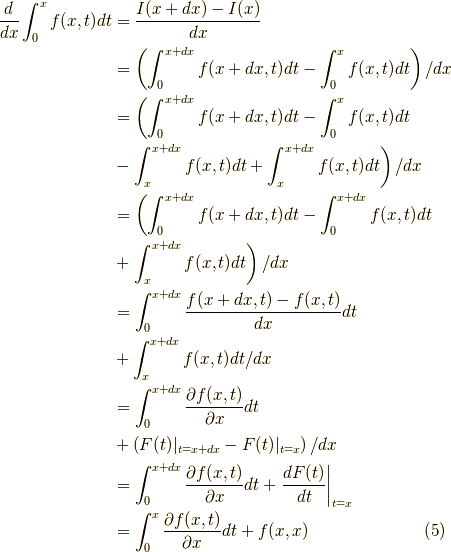
よって結果だけを書くと,
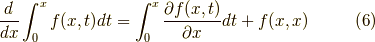
となります.これだけではちょっと不安なので,同じ計算を別の方法でやってみます.
証明2:多変数の微分として見る
まず,  と
と 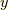 をパラメータ
をパラメータ  の変数としてみます.最後に
の変数としてみます.最後に 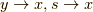 とします.そこで,考えるのは
とします.そこで,考えるのは
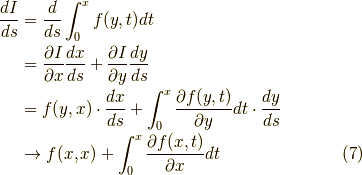
となり,同じ結果になりました.どうやら正しそうですね.一応注意しておくと, 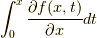 は,
は, 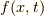 を
を 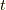 を定数と見て
を定数と見て  で偏微分したのち,今度は
で偏微分したのち,今度は  を定数と見て
を定数と見て 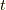 で積分したものです.
で積分したものです.
証明3:合成関数の微分として見る
基本的には証明2と同じですが,よりシンプルだということで記しておきます.
積分の二つのxを別の変数と見て,二変数の関数  と
と 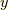 との関数と見なします.どちらを
との関数と見なします.どちらを 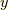 としても最後に
としても最後に 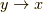 とするので,同じことになります.すると,求めたい微分は
とするので,同じことになります.すると,求めたい微分は
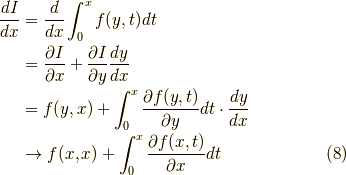
と同じ結果となります.
具体例で確かめる
では,得られた結果を具体例で確認してみましょう.  を計算してみます.
を計算してみます.
![\dfrac{d}{dx} \int_0^x f(x,t)dt &= \dfrac{d}{dx} \int_0^x x e^{-t} dt \\&= \dfrac{d}{dx} \left[ -x e^{-t} \right]_{t=0}^{t=x} \\&= \dfrac{d}{dx} \left( -x e^{-x} + x \right) \\&= (x-1) e^{-x} + 1 \tag{9}](./aa9f6f65aa31ea0bf62a213702b35107.png)
となります.ここで,  であり,
であり, 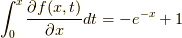 ですから,両者は一致します.
ですから,両者は一致します.
畳み込み積分の微分
関数  の畳み込みとは以下のような積分になります.
の畳み込みとは以下のような積分になります.
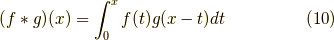
これは, 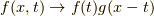 として,先ほど得られた結果を用いれば良く,
として,先ほど得られた結果を用いれば良く,
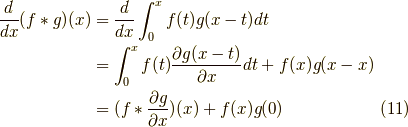
と分かります.それでは,今日はこの辺で.お疲れ様でした.