行列式
行列式についての定義,そしてそれを展開する方法,ベクトル積との関係について説明します.
行列式の定義
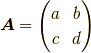
という行列 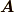 があった場合,行列式はつぎのように定義されます.
があった場合,行列式はつぎのように定義されます.
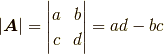
行列式は行列の成分同士の演算ですから,ベクトルではなく単なる値(スカラー量)です. 下のように書いても,上式と同じ意味です.
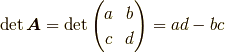
また, det とは行列式を表す単語 determinant の略です.
行列式の展開
定義から2次の行列式ならすぐに求めることができますが, 3次以上の場合にはそうもいきません. そこで,3次以上の行列式を2次以下に展開する方法があります. それは小行列式展開と呼ばれる方法です.たとえば,つぎのように展開できます.
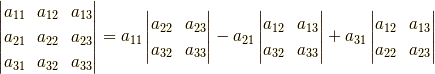
何をやっているのか良く分かりませんね. これは第1列について展開しているんですが, じっくり見ると規則性があることに気付きます.
係数について見てみます.まずは 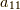 についてです.
についてです.

右辺第1項の係数には 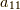 が出てきてます.
そしてそれに付随する小行列式は
が出てきてます.
そしてそれに付随する小行列式は 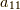 が含まれている
1行目と1列目が取り除かれた形になってます.
が含まれている
1行目と1列目が取り除かれた形になってます.
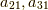 についても同様のことがいえます.
についても同様のことがいえます.
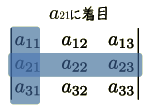

符号について見てみます.第1行1列(左上)をプラス,
そこから下または右に1つ進むと符号が反転すると決められています.
たとえば 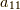 は左上にあるのでプラス,
は左上にあるのでプラス, 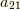 は1つ下に行くのでマイナス,
は1つ下に行くのでマイナス,
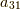 は2つ下に行くのでプラスになります.
は2つ下に行くのでプラスになります.
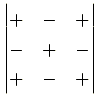
係数と符号は第1列以外で展開しても全く同じように成り立ちます. たとえば第2行で展開すれば
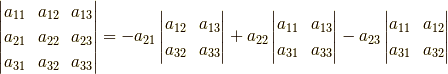
となります.
ベクトル積と行列式
覚えにくいベクトル積も,行列式を使えば簡単に覚える事ができます.ベクトル積の定義は
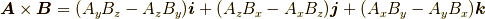
です.慣れないうちは各成分の中身がこんがらがってしまいます.
でもよく見てみると行列式で書けることに気付きます.
 は行列式で書くと
は行列式で書くと
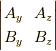 ですね
(よく分からなければ逆に行列式を計算して確かめてみてください).
同様に他の成分も行列式で書くと
ですね
(よく分からなければ逆に行列式を計算して確かめてみてください).
同様に他の成分も行列式で書くと
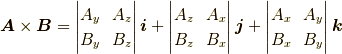
となります.少し覚えやすそうになりました. さらに,先ほどの小行列式展開の逆を行います (この操作の前にjの符号を変えています.理由はあとで分かります).
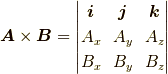
行ごとに  ,
, 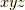 と順番に並んでいるので,これなら覚えやすいです.
ベクトル積の成分を使うときにはこれを展開して2次の行列式にしてやり,
行列式の計算をすればいいわけです.
ためしに展開してもとに戻してみます.
と順番に並んでいるので,これなら覚えやすいです.
ベクトル積の成分を使うときにはこれを展開して2次の行列式にしてやり,
行列式の計算をすればいいわけです.
ためしに展開してもとに戻してみます.  に着目して展開するとそれぞれの係数は
に着目して展開するとそれぞれの係数は
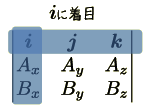


ですから
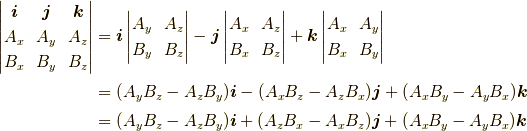
となり,元に戻りましたね. 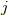 の符号を変えた理由も分かると思います.
の符号を変えた理由も分かると思います.
rotと行列式
ベクトル積と同様にベクトル解析のrotも行列式で覚えられます.
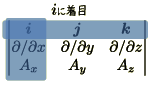
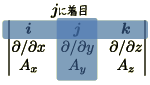
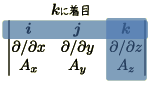
より
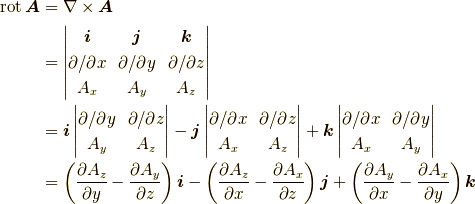
のように表記することができます.