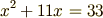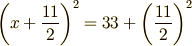平方完成の図形的イメージ
2次方程式を解く 際,「平方完成」という操作を行います. はじめて授業で習ったとき,どうも変形の本質というか, イメージが掴めなかった方も多いのではないでしょうか. 平方完成の“図形的イメージ”を捉えることを目標に,この記事を書きました.
平方完成とは
2次方程式を解くときに,「なんとかの二乗=定数」という形に変形することを,平方完成と呼びます. たとえば
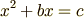
という2次方程式を平方完成すると,
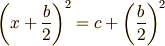
になります.この式変形の意味を,何とか図形的にイメージすることはできないでしょうか.
図形的意味
一般式ではイメージし辛いので,つぎのように具体的な2次方程式を考えます.

この式の意味は「ある数を二乗したものと,ある数に11を掛けたものを足すと,33である」ということです. そして,方程式の解を求めるとは,「ある数」が具体的にいくらなのかを決めることです. 式 (1) をなんとか図形的に表したいのですけど,どうしよう. そうだ,“2次”なのだから,面積に例えられないでしょうか. 四角形の面積は,一辺掛ける一辺,という2次の問題です. 特に正方形ならば,辺の長さの二乗,という問題になります. 2次方程式を,正方形の面積を求める問題 [*] に置き換えてみましょう.
| [*] | この図形的な方法は,アラビアのアル・クワリズミという数学者が考えたそうです. ちなみに,“アル・クワリズミ”は“アルゴリズム”の語源だとか. |
正方形とその面積
まずは式 (1) の右辺を,正方形の面積として表現することにします. 正方形の絵を描いておきます.

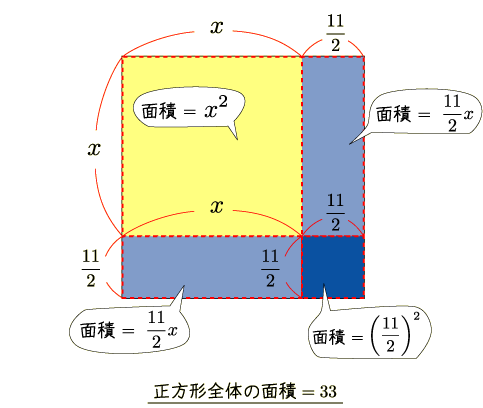
残るは式 (1) の左辺を,正方形の辺の長さで表せれば, 2次方程式を図形的に表したことになります.しかし式 (1) の左辺は
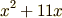
なので,正方形の辺の長さにする,と言ってもなんだか良くわかりません.
しかしこれが 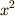 だったらどうでしょう.この場合,辺の長さは
だったらどうでしょう.この場合,辺の長さは  で良いですよね.
一辺の長さが
で良いですよね.
一辺の長さが  の正方形の面積は,
の正方形の面積は, 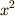 ですからね.
ですからね.
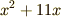 を「何とかの二乗」に近づけるため,つぎの式変形を行います.
を「何とかの二乗」に近づけるため,つぎの式変形を行います.

ひとまず,「何とかの二乗」に近づきました. マイナスが付いた項が出てくるのは,両辺の値を等しくするためです. 式 (2) の右辺を式 (1) の左辺に代入してみましょう.
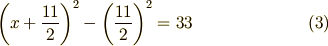
となります.
仮にマイナスの項を無視して考える
ここで一時的に,式 (3) においてマイナスの項を「なかったこと」にして考えてみると
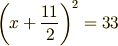
であり,この式は,図形的につぎの図で表せます.
一辺の長さが 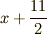 の正方形ですね.
の正方形ですね.
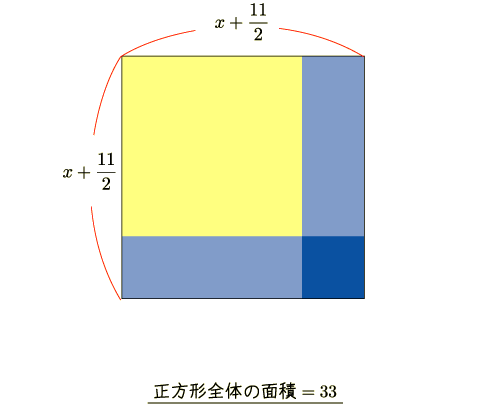
色分けしているのにはちゃんと意味があります. 図にもう少し情報を書き込んでみます.
一辺の長さが 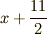 であるという情報を元に,
このように,全体を4つの四角形に分けることができます.
であるという情報を元に,
このように,全体を4つの四角形に分けることができます.
- 面積
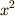 の正方形が1つ
の正方形が1つ - 面積
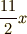 の長方形が2つ,
の長方形が2つ, - 面積
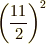 の正方形が1つ
の正方形が1つ
です.図の右下の,面積 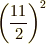 の正方形に注目してください.
の正方形に注目してください.
マイナスの項もちゃんと考える
マイナスの項をちゃんと考えるには,両辺に「マイナスの項と同じもの」 を足して打ち消す,という方針を取ります.つまり
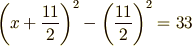
を
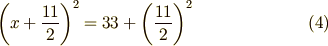
とすれば良いのですね.いまの場合,まるっきり無視したのではなく, 左辺から引いた分を右辺に足しているので,方程式の整合性は保たれています. しかし今度は,全体の面積に相当する右辺の値が増えてしまいました. これは,つぎの図のように考えます.
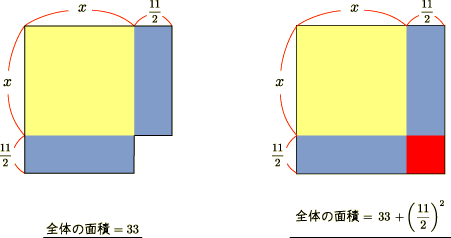
左側の「一部が欠けた正方形」の面積こそが,式 (1) の右辺に相当し, 右側の「ちゃんとした正方形」が,変形した式 (4) の右辺に相当している,ということです.