直交関数系

関数が直交するということ

関数が直交するということを， 相関関数 を計算することによって，知ることが出来ます．どういうときに，「関数が直交している」といえるのか，もう一度見てみることにしましょう．

[*]相関関数の記事で，直交関数のことに触れています．時間のある方は，こちらも読まれることをお勧めします．

二つの実関数 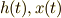h(t),x(t) が直交しているということを，相対関数を使って

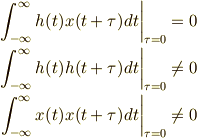
\int^{\infty}_{-\infty}h(t)x(t+\tau)dt \biggr|_{\rm{\tau=0}} &= 0\\\int^{\infty}_{-\infty}h(t)h(t+\tau)dt \biggr|_{\rm{\tau=0}} &\neq 0\\\int^{\infty}_{-\infty}x(t)x(t+\tau)dt \biggr|_{\rm{\tau=0}} &\neq 0

と表現できましたね．

直交関数系

ある関数列(関数の集合) 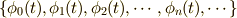\{\phi_0(t),\phi_1(t),\phi_2(t),\cdots,\phi_n(t),\cdots \} が存在し，そのうち，任意の二つの関数を取り出して \tau=0 のときの相関関数の値が

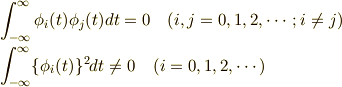
& \int^{\infty}_{-\infty}\phi_i(t)\phi_j(t)dt = 0 \hspace{0.5cm} (i,j=0,1,2,\cdots;i\neq j)\\ & \int^{\infty}_{-\infty}\{ \phi_i(t) \}^2 dt \neq 0 \hspace{0.5cm} (i=0,1,2,\cdots)

となる関数列を 直交関数系 といいます．つまり，お互いに直交関数となっている関数列の集まりなんですね． また，直交関数系の特別な場合として 正規直交関数系 というのがあります．

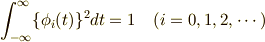
\int^{\infty}_{-\infty}\{ \phi_i(t) \}^2 dt=1 \hspace{0.5cm} (i=0,1,2,\cdots)

になる関数列のことです．「正規･･･」となっているんですから，この関数列は何かの基準になってくれそうな匂いが致しますね．くんくん．

[†]今回は一般的な議論として，関数の区間を特に決めずに話を進めてきましたが，具体的な関数列を考える場合は，その関数列が周期性を持っているか，どんな区間で存在しているかを考慮して積分範囲を定める必要があります．

さて，ここまでは直交関数系というものを定義で見てきました．直交関数というものは，お互いに関数の内積を取ったとき(お互いの相関を取ったとき)に 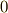0 になるというものでした．「関数の内積」に慣れない方は， 内積空間 の記事中の「内積の概念を拡張」のセクションをご覧ください．

Important

直交関数は，互いに関数の内積を取ると0になる関数である．

この性質から，直交関数系というものは，何かもっと面白い意味があるんじゃないかということが想像されます．例えば，同じ内積をとるベクトル空間では，互いに直交しているベクトルを使って，任意のベクトルを表すことが出来ます． これと同じように，直交している関数列を使って，任意の関数を表現できないのでしょうか？？？

答えは，次のセクションを読んでみて下さい．

直交関数系から

直交関数系の関数列が，ベクトル空間の単位ベクトルと同じ働きをするかどうか，それを検討していきましょう．

ベクトル空間で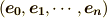， (\bm{e_{0}},\bm{e_{1}},\cdots,\bm{e_{n}}) を単位ベクトルに取る場合を考えます．この単位ベクトルに直交関数系のように，ある規則を付け加えておきましょう．すなわち，

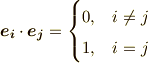
\bm{e_{i}}\cdot \bm{e_{j}} = \begin{cases} 0 , & i \neq j\\ 1, & i=j \end{cases}

このとき，単位ベクトル 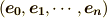(\bm{e_{0}},\bm{e_{1}},\cdots,\bm{e_{n}}) は1次独立であり，ゆえに任意のn次ベクトルを単位ベクトルの線形結合で以下のように表すことが出来ます．(1次独立や線形結合の意味が分からない場合は，線形代数を復習してみてください．)

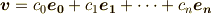
\bm{v}=c_0\bm{e_{0}}+c_1\bm{e_{1}}+\cdots+c_n\bm{e_{n}}

しつこく書きますが，直交関数系(今の場合は正規直交関数)では，

\int^{\infty}_{-\infty}\phi_i(t)\phi_j(t)dt=\begin{cases}0 ,& i\neq j \\ 1 ,& i=j\end{cases}

ですね．これらの関数を用いて，ある関数 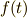f(t) を作ったとすると，

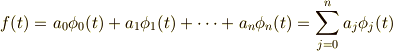
f(t)=a_0\phi_0(t)+a_1\phi_1(t)+\cdots+a_n\phi_n(t)=\sum_{j=0}^n a_j \phi_j(t)

ここでは，まだ 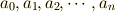a_0,a_1,a_2,\cdots,a_n は，一意のものであるとは限りません．もしかしたら，何通りか組み合わせがあるかもしれないものとしましょう．ただし，関数列は正規直交関数列であるということは，しっかり覚えておきましょう．

このとき 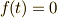f(t)=0 とおき，右辺は項別積分が可能な関数列として，両辺の 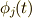\phi_j(t) との相関をとってやると，

\int^{\infty}_{-\infty} f(t)\phi_j(t) dt &= \int^{\infty}_{-\infty} \sum_{k=0}^{n} a_k \phi_j(t)\phi_k(t) dt\\ &= a_j

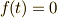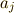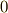上の式は f(t)=0 であることから，このときすべての a_j について 0 しか取りえないということが言えます．つまり，関数列 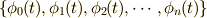\{\phi_0(t),\phi_1(t),\phi_2(t),\cdots,\phi_n(t)\} は， 1次独立 であることが分かりますね．

ふむふむ．注目すべき事実が分かってきました．関数列が単位ベクトルなどと同じ1次独立なのですから，この関数列で，ある関数 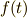f(t) を表そうとすると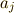， a_j は何通りかあるのではなく，一意に決定できますね．そうです，直交関数系を使えば，ベクトル空間でもあったような，「任意のn次ベクトルを単位ベクトルの線形結合で表す」のと同じことができるのです!!

theorem

直交関数系の各関数の線形結合で，一意的に関数を表すことができる．