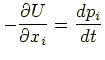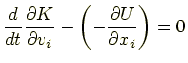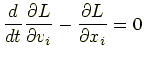ラグランジュアン
ニュートンの方程式は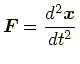 であるが,
左辺の力は(保存力であれば)ポテンシャルエネルギー
であるが,
左辺の力は(保存力であれば)ポテンシャルエネルギー 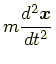 は運動量
は運動量 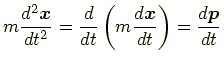 と書ける.
以上より,ニュートンの運動方程式は
と書ける.
以上より,ニュートンの運動方程式は
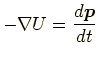 |
と表せる.これをベクトルの成分で表すと
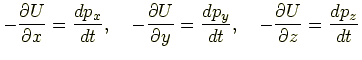 |
である.ここで添字を
となる.右辺はエネルギーを使って表せているので右辺もエネルギーで表すことを考える. 運動エネルギー
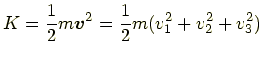 を
を 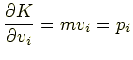 |
であるから,これを式(1.9)に代入すると
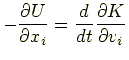 すなわち
すなわち
となる.ここで
| (1.19) |
なる量を導入する.これをラグランジュアンという. すると式(1.18)はもっと簡単な表現
で書ける.式(1.20)はオイラー・ラグランジュの方程式または単に ラグランジュ方程式と呼ばれる.
物理のかぎプロジェクト / 平成18年3月2日