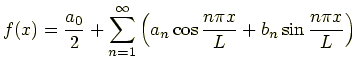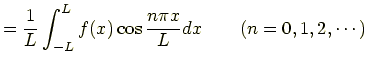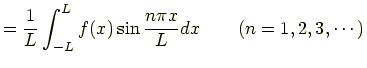フーリエ級数

任意の周期関数を三角関数の無限級数で表すのがフーリエ級数である． 区間 $(-L, +L)$ の任意の周期関数 $f(x)=f(x+2L)$ は

$$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left(a_n\cos\frac{n\pi x}{L} +b_n\sin\frac{n\pi x}{L}\right)$$ (10.1)

と表される．ただし

$$a_n =\frac{1}{L}\int_{-L}^{L}f(x)\cos\frac{n\pi x}{L}dx \qquad (n=0,1,2,\cdots)$$ (10.2)

$$b_n =\frac{1}{L}\int_{-L}^{L}f(x)\sin\frac{n\pi x}{L}dx \qquad (n=1,2,3,\cdots)$$ (10.3)

である．

フーリエ級数の複素表示

三角関数よりも指数関数を使った方が便利なことは物理において多々あることで， フーリエ級数もそういった場合がある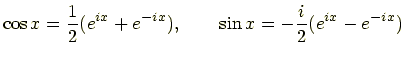．$\cos x$，$\sin x$ はオイラーの公式から

$$\cos x = \frac{1}{2}(e^{ix}+e^{-ix}), \qquad \sin x = -\frac{i}{2}(e^{ix}-e^{-ix})$$ (10.4)

と表せるので，これを式(10.1)に代入すると

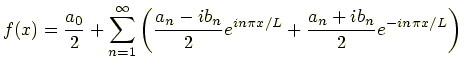$$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty} \left(\frac{a_n-ib_n}{2}e^{in\pi x/L} + \frac{a_n+ib_n}{2}e^{-in\pi x/L}\right)$$ (10.5)

となる．ここで

$$c_0 = \frac{a_0}{2}, \qquad c_n = \frac{a_n-ib_n}{2}, \qquad c_{-n} = \frac{a_n+ib_n}{2} \qquad (n=1,2,3,\cdots)$$

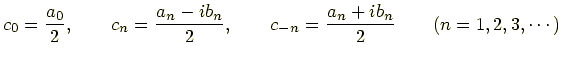とおくとフーリエ級数は複素数を使って

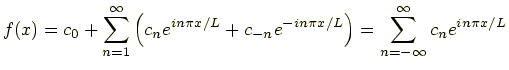$$f(x) = c_0 + \sum_{n=1}^{\infty}\left(c_ne^{in\pi x/L}+c_{-n}e^{-in\pi x/L}\right) = \sum_{n=-\infty}^{\infty}c_ne^{in\pi x/L}$$ (10.6)

で表される．ただし $c_n$ の定義と式(10.2)，(10.3)から

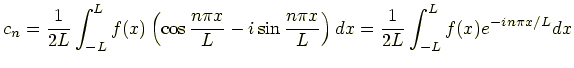$$c_n = \frac{1}{2L}\int_{-L}^{L}f(x)\left(\cos\frac{n\pi x}{L}-i\sin\frac{n\pi x}{L}\right)dx = \frac{1}{2L}\int_{-L}^{L}f(x)e^{-in\pi x/L}dx$$ (10.7)

である．