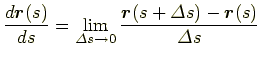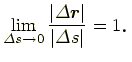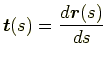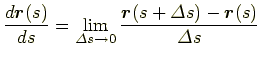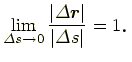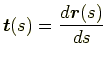曲線上の近接した2点
をとり,
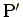
を限りなく
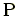
に近づけるとき,
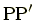
を延長した直線は曲線に接した直線になる.これを接線
という.
また P において接線と直交する直線を法線
という.
曲線上の2点
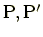
の位置ベクトルを
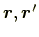
とすると,
ベクトル
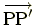
は
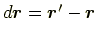
で表される.
曲線上のある点から運動の向きに測った弧の長さを
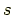
とすると,
点
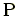
の位置ベクトルは
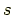
の関数として
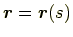
で与えられる.そうすると
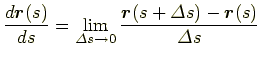 |
(7.20) |
は点
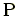
における曲線の接線ベクトル
である.
また,
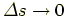
の極限では弧の長さ
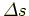
と
ベクトル
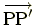
の長さは等しくなる
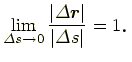 |
(7.21) |
したがって,
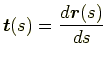 |
(7.22) |
は単位接線ベクトルである.
物理のかぎプロジェクト / 平成19年1月14日