内部積とは
この記事では,内部積と言う概念に慣れる目的で色々と調べてみます. 内部積とは,反微分とも呼ばれる操作です. どうもピンと来ないので色々確かめてみました.
本論
まず,多様体 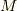 を考えます.
を考えます. 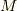 上の r-形式全体の集合を
上の r-形式全体の集合を 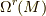 と
します.ここで内部積
と
します.ここで内部積 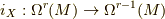 の定義は以下です.
の定義は以下です.
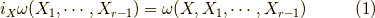
です.ベクトル 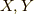 とr-形式
とr-形式  を以下の様に取ります.
を以下の様に取ります.
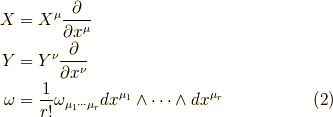
下の参考文献によると,内部積は

とのことです.これについてこれから調べていきます.
ここで  はこの一形式を削除するという意味です.
ここで
はこの一形式を削除するという意味です.
ここで  の重要な性質として,
任意の添え字の互換に対して反対称であることが挙げられます.
つまり,
の重要な性質として,
任意の添え字の互換に対して反対称であることが挙げられます.
つまり,

等が言えます.
さて,まずは基本に忠実に  を書き下してみましょう.以下では三次元空間中の2-形式
を書き下してみましょう.以下では三次元空間中の2-形式  を考えます.
を考えます.
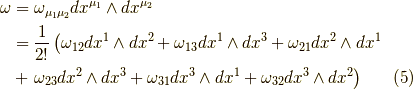
であって,各々のウェッジ積 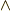 は
は
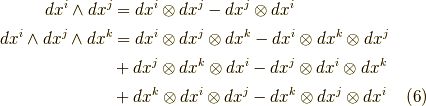
等とテンソル積の組み合わせになっており,符号は 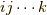 の偶置換なら
の偶置換なら  奇置換なら
奇置換なら  を取ります.
三次のウェッジ積は3つのベクトルのスロットがあり,そこにベクトルが
入ることで
を取ります.
三次のウェッジ積は3つのベクトルのスロットがあり,そこにベクトルが
入ることで 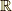 の元が返ります.
の元が返ります. 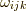 も
も 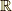 の元です.
の元です.
式 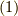 で
で 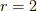 とすると,右辺は
とすると,右辺は 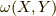 を考えれば良さそうです.
上手い書き方が無いので,ここで自分で決めておきます.
まず,ベクトルの基底を
を考えれば良さそうです.
上手い書き方が無いので,ここで自分で決めておきます.
まず,ベクトルの基底を 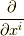 を
を 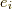 で書きます.
一形式の基底は
で書きます.
一形式の基底は  で書きます.
そして,今後の計算で
で書きます.
そして,今後の計算で 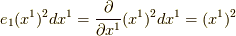 です.
です. 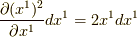 等の計算は発生せず,
ただ,基底同士が数値になるだけです.
式
等の計算は発生せず,
ただ,基底同士が数値になるだけです.
式 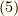 で
で 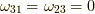 の時を考えると,
の時を考えると, 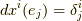 で
で 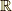 が取り出されるものとして考えます.基本的な場合から考えます.
が取り出されるものとして考えます.基本的な場合から考えます.

同様に 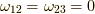 に対して,
に対して,

最後に 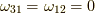 に対して,
に対して,

が返ります.  がどんな形をしていようと,
がどんな形をしていようと, 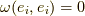 となります.
また,
となります.
また,  には多重線形性がありますから,
には多重線形性がありますから,
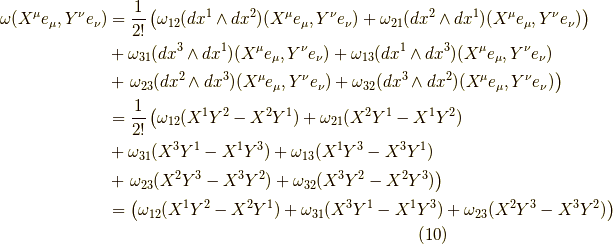
となります.ここで,内部積は一般的には最初のスロットにだけベクトルが入ったものです.
つまり,上式で 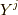 を
を 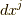 に変えたものが求めたいものです.
に変えたものが求めたいものです.
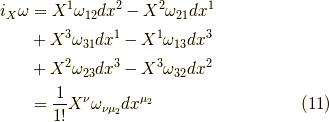
つまり,これは 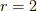 の時の式
の時の式 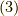 の一番目の等号が示せたことになります.
の一番目の等号が示せたことになります.
これだけでは不安なので,  次元中の
次元中の 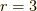 の場合も示しておきましょう.
の場合も示しておきましょう.

と略記します.式 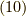 にならって,
にならって,

となります.この式  は,
は, 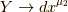 と
と 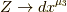 でスロットを
空にすれば,
でスロットを
空にすれば, 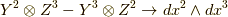 等が成立しましたから,
等が成立しましたから,
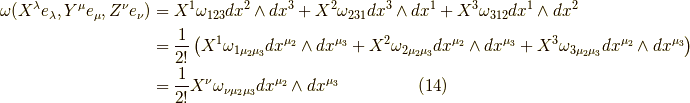
となります.これで今回も式  の一番目の等号が示せました.
の一番目の等号が示せました.
式 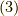 の二番目の等号については,再掲しておくと,
の二番目の等号については,再掲しておくと,
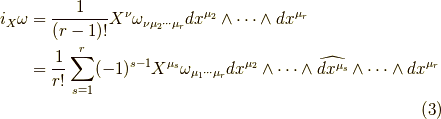
なのでした.異なる  に対して,微分形式の基底部分は
に対して,微分形式の基底部分は
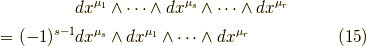
と変形できます.
ベクトル 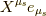 は一番左のスロットに来た
は一番左のスロットに来た 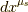 に作用し,
実数値である
に作用し,
実数値である 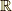 の元になります.
それぞれの
の元になります.
それぞれの  に対して
に対して 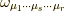 はこの添え字たち関して反対称ですから,
はこの添え字たち関して反対称ですから,  を合わせて,同じ絶対値で符号も同じ項が
を合わせて,同じ絶対値で符号も同じ項が  個出来ることになります.
それらの和記号
個出来ることになります.
それらの和記号 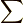 を導入しても等号で両辺を結ぶには
を導入しても等号で両辺を結ぶには  で割る必要があり,階乗の因子は
で割る必要があり,階乗の因子は 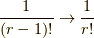 に変わります.そうして,二番目の等号が示せました.
に変わります.そうして,二番目の等号が示せました.
具体例
具体例を考えます.スロットの一番目のみを埋めるということに注意してください.
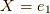 の時,
の時,
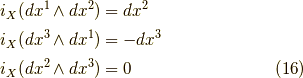
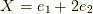 の時,
の時,

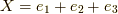 の時,
の時,
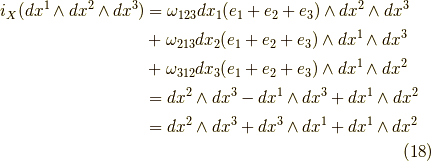
いかがだったでしょうか?内部積を理解できたとしたら幸いです. 今日はここまで,お疲れさまでした.