整数の剰余類のつくる加群
整数全体の加群 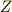 を,自然数
を,自然数  を法として類別した剰余類を考えます.このとき,異なる剰余類に属する二つの整数
を法として類別した剰余類を考えます.このとき,異なる剰余類に属する二つの整数 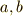 について,次の演算が成り立ちます.
について,次の演算が成り立ちます.
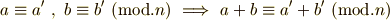
proof
左辺より,ある整数を使って 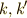 を使って,
を使って, 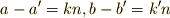 と表わせるはずです.このとき
と表わせるはずです.このとき 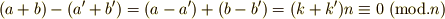 が示せます.∴
が示せます.∴ 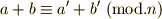 ■
■
ある剰余類の元に他の剰余類の元を足したものが,やはりどこかの剰余類に属する元になることが分かりましたので,どうやら整数の加群の剰余類は,剰余類同士の演算について閉じているようです.
このように,剰余類と剰余類を足すという加法演算を,『剰余類の集合』に導入しましょう. この加法演算には単位元があります( 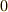 を含む剰余,すなわち余りが零の剰余類です).また,逆元もあります(
を含む剰余,すなわち余りが零の剰余類です).また,逆元もあります(  を含む剰余類に
を含む剰余類に 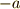 を含む剰余類を足すと,余りが零の剰余類になってしまいます).
を含む剰余類を足すと,余りが零の剰余類になってしまいます).
よって,この剰余類の集合は,加法に関して群になっていることが分かりました.これを nに関する剰余類群 と呼び, 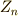 で表わします.
で表わします.
| [*] | 一つ一つの剰余類は集合ですが,一般に剰余類自身は群にはなりません.ところが,このように剰余類の集合(つまり,集合の集合!)を考えると,うまく群になったりするんですね.集合の集合,集合の集合の集合,のようなものをいくらでも考えられるのが,抽象数学の素晴らしさです. |
有限巡回群との同型
剰余類の辺りから少し話が抽象的になりましたから,剰余類群という,とても抽象的な群を求めたように感じるかも知れないのですが,実は,  に関する剰余類群
に関する剰余類群 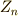 は,
は,  次の有限回転群と同型(つまり有限巡回群と同型)で,もう読者のみなさんが知っている群なのです.面白いことです!
次の有限回転群と同型(つまり有限巡回群と同型)で,もう読者のみなさんが知っている群なのです.面白いことです!
整数と聞いて,数直線状にまっすぐ数が並んでいるイメージしか持っていないと,ピンとこないかもしれません.しかし,次の図を見れば,剰余類の加法が,有限回転変換に対応させられることが納得いくと思います.
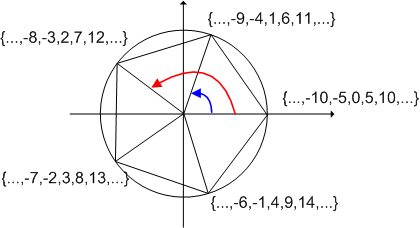
あるいは,一直線の数直線を,周の長さが 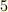 の円筒にグルグル巻き付ければ,この図のようになると考えても良いでしょう.
の円筒にグルグル巻き付ければ,この図のようになると考えても良いでしょう.
| [†] | n次の有限巡回群を一般に 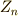 と書くと, 有限巡回群 のページで触れましたが,このような事情があったのですね. と書くと, 有限巡回群 のページで触れましたが,このような事情があったのですね. 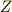 は整数(ドイツ語で は整数(ドイツ語で 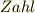 )の意味です. )の意味です. |
| [‡] | 整数は無限にあるわけですが,整数全体を 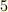 で割ったときの剰余は, で割ったときの剰余は, 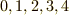 の の 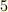 種類しかありません.しかもその剰余はグルグル循環します.そう考えると,有限巡回群と同型だというのも至極当然だと分かります. 種類しかありません.しかもその剰余はグルグル循環します.そう考えると,有限巡回群と同型だというのも至極当然だと分かります. |