四次方程式
二次方程式,三次方程式に引き続き,四次方程式も考えてみます.四次方程式にも解の公式が存在することは,読者のみなさんは御存知だと思いますので,この記事が,方程式が代数的に解ける場合の最後の例となります.ガロア理論を復習しながら,できれば記事を読む前に,自分で解を導けるくらいの勢いで読んで欲しいと思います.中間体が三つも出てきますから,三次方程式と比べて,議論は桁違いに複雑です.
四次方程式
次の形の四次方程式の解を考えます.係数  は体
は体  の元とします.
の元とします.
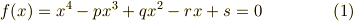
体  は
は 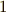 の四乗根を全て含むものとし,
の四乗根を全て含むものとし,  の最小分解体を
の最小分解体を  とします.ガロア群
とします.ガロア群  は,
は,  の解
の解 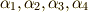 を置換する対称群で,
を置換する対称群で, 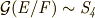 が言えます.これより,
が言えます.これより, ![[E:F]=|\cal G \rm (E/F)|=|S_{4}|=24](./be4ee5148609f799e9b6a328e47bc4e3.png) が分かります.(この辺りの議論は, 二次方程式 や 三次方程式 と全く同じです.)
が分かります.(この辺りの議論は, 二次方程式 や 三次方程式 と全く同じです.) 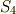 の正規部分群の組成列としては,次のような列が考えられます.
の正規部分群の組成列としては,次のような列が考えられます.
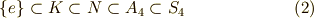
一応,それぞれの群の要素を書き出しておきます.それぞれ正規部分群になっていることを確認して下さい.

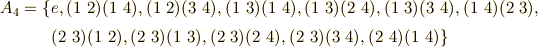
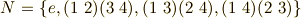
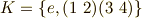
念のため, 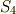 が可解群であることを確認してみましょう.
が可解群であることを確認してみましょう. 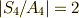 より,
より, 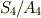 が可換群であることは明らかでしょう.また,
が可換群であることは明らかでしょう.また,  で,これは巡回群ですから,もちろん可換群です.(ちゃんと確認してみましょう.)
で,これは巡回群ですから,もちろん可換群です.(ちゃんと確認してみましょう.) 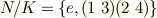 もちゃんと可換群になっています.これより,
もちゃんと可換群になっています.これより, 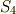 は可解群であることが確かめられました.式
は可解群であることが確かめられました.式  の四次方程式は,代数的に解けることが分かったわけですが,このままラグランジェのリゾルベントを定義通り考えるのは大変すぎるので,少し工夫します.いま,これらガロア群の正規部分群に対して,それぞれ固定体となる中間体
の四次方程式は,代数的に解けることが分かったわけですが,このままラグランジェのリゾルベントを定義通り考えるのは大変すぎるので,少し工夫します.いま,これらガロア群の正規部分群に対して,それぞれ固定体となる中間体  を考えることが出来ます.
を考えることが出来ます.
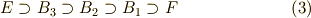
ここで,交代群 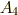 によって,次式で定義される
によって,次式で定義される 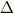 は不動に保たれ,
は不動に保たれ, 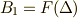 だと考えることが出来ます.
だと考えることが出来ます.

| [*] | 蛇足ですが, 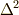 は は 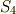 で不動ですので, で不動ですので,  の元だということが分かります. の元だということが分かります. |
群 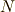 によって不動に保たれるのは,次のような元です.
によって不動に保たれるのは,次のような元です.



群 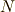 の元は
の元は 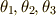 をそれぞれ不動に保ちますが,
をそれぞれ不動に保ちますが, 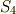 の他の元は,
の他の元は, 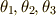 をそれぞれ違いに移します.これより,次の関係が分かります.
をそれぞれ違いに移します.これより,次の関係が分かります.

この 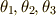 を使って,次のような方程式を考えてみましょう.
を使って,次のような方程式を考えてみましょう.
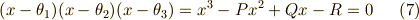
ただし,式中の係数は次のように置いています.
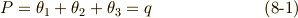
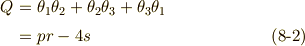
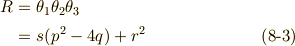
右辺二行目の  による表現では,解と係数の関係を使っていますが,詳細な計算は面倒なので省略させて下さい.気になる人は代入してみれば確認できると思います.解と係数の関係は,式
による表現では,解と係数の関係を使っていますが,詳細な計算は面倒なので省略させて下さい.気になる人は代入してみれば確認できると思います.解と係数の関係は,式 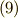 として示しておきます. 三次方程式は解ける わけですから,
として示しておきます. 三次方程式は解ける わけですから,  は
は 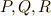 だけで表すことができ,これは,すなわち
だけで表すことができ,これは,すなわち  だけで表わすことが出来るということです.
だけで表わすことが出来るということです.
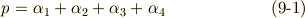
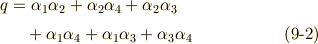


方程式 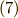 の解は
の解は 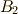 の解ですが,
の解ですが, 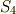 によって式
によって式 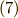 は不動に保たれます.そこで,
は不動に保たれます.そこで, 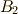 は,
は,  上の方程式
上の方程式 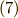 の最小分解体だと考えることが出来ます.式
の最小分解体だと考えることが出来ます.式 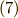 を 三次分解方程式 と呼び, フェラーリの方法 の途中で考えるものです.式
を 三次分解方程式 と呼び, フェラーリの方法 の途中で考えるものです.式  の解を表わすのに
の解を表わすのに 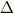 を直接使わず,
を直接使わず, 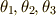 を使うことになります.さて,ここで次式のように
を使うことになります.さて,ここで次式のように 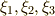 を定義します.
を定義します.

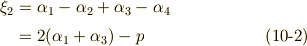
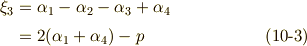
この 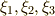 と式
と式  によって,式
によって,式  の解
の解 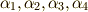 は次のように表わすことが出来ます.
は次のように表わすことが出来ます.
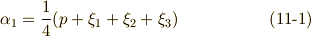
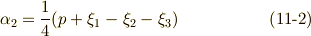
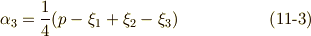
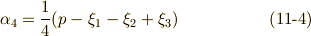
あとは 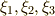 を
を  で表わせれば良いわけですが,解と係数の関係を使うと,次のような関係が分かります.(細かい計算は省略します.省略ばかりでスミマセン.)
で表わせれば良いわけですが,解と係数の関係を使うと,次のような関係が分かります.(細かい計算は省略します.省略ばかりでスミマセン.)



式 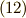 の平方根を取り,既出の三次分解方程式の解
の平方根を取り,既出の三次分解方程式の解 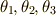 を代入すれば,確かに
を代入すれば,確かに 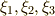 は
は  だけで表わせるという道筋が見えます.あとは,代入するだけです.これ以上の計算は骨折りなので,ここで終わりにさせてください.(・_・)
だけで表わせるという道筋が見えます.あとは,代入するだけです.これ以上の計算は骨折りなので,ここで終わりにさせてください.(・_・)
| [†] | 群 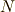 の元は, の元は, 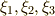 は符号を は符号を  と変えます.つまり,二乗すれば群 と変えます.つまり,二乗すれば群 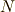 の元によって の元によって 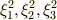 の符号は変わらないので, の符号は変わらないので, 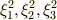 は は 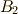 の元だということが分かります. の元だということが分かります. |