三次方程式の解の公式
二次方程式の解の公式は学校で必ず習いますが,三次方程式の解の公式は習いません.でも,三次方程式と四次方程式は,ちゃんと解の公式で解くことができます.学校で三次方程式の解の公式を習わないのは,学校で勉強するには複雑すぎるからです.しかし,三次方程式の解の公式の歴史にはドラマがあり,そこから広がって見えてくる豊潤な世界があります.そのあたりの展望が見えるところまで,やる気のある人は一緒に勉強してみましょう.
立体完成
二次方程式を勉強したとき, 平方完成 という操作がありました.  の一次の項を,座標変換によって表面上消してしまう操作です.
の一次の項を,座標変換によって表面上消してしまう操作です.
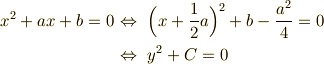
ただし,最後の行では,確かに一次の項が消えてしまったことを見やすくするために, 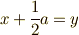 ,
, 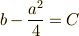 と置き換えました.ここまでは復習です.( 平方完成の図形的イメージ 参照.)
と置き換えました.ここまでは復習です.( 平方完成の図形的イメージ 参照.)
これと似た操作により,三次式から  の二次の項を表面上消してしまう操作を 立体完成 と言います.次のように行います.
の二次の項を表面上消してしまう操作を 立体完成 と言います.次のように行います.
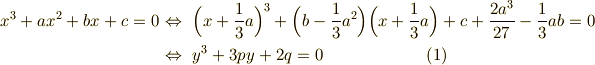
ただし,最後の行では,見やすくするために, 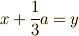 ,
, 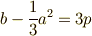 ,
, 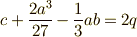 と置き換えました.カルダノの公式と呼ばれる三次方程式の解の公式を用いるときは,まず立体完成し,式(1)の形にしておきます.
と置き換えました.カルダノの公式と呼ばれる三次方程式の解の公式を用いるときは,まず立体完成し,式(1)の形にしておきます. 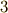 とか
とか 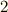 という係数をつけたのは,後々の式変形の便宜のためで,あまり意味はありません.
という係数をつけたのは,後々の式変形の便宜のためで,あまり意味はありません.
カルダノの公式の歴史1
カルダノの公式と呼ばれる三次方程式の解の公式が発見されるまでの歴史は大変興味深いものですので,少しここで紹介したいと思います.二次方程式の解(虚数解を除く)を求める公式は,古代バビロニアにおいて,既に数千年前から知られていました.その後,三次方程式の解の公式を探す試みは,幾多の数学者によって試みられたにも関わらず,16世紀中頃まで成功しませんでした.式(1)の形の三次方程式の解の公式を最初に見つけたのは,スキピオーネ・フェロ(  )だったと言われています.しかし,フェロの解法は現在伝わっていません.当時,一定期間内により多くの問題を解決した者を勝者とするルールに基づき,数学者同士が難問を出し合う一種の試合が流行しており,数学者は見つけた事実をすぐに発表せず,次の試合に備えて多くの問題を予め解いて,秘密にしておくのが普通だったのです.フェロも,解法を秘密にしているうちに死んでしまったのだと考えられます.
)だったと言われています.しかし,フェロの解法は現在伝わっていません.当時,一定期間内により多くの問題を解決した者を勝者とするルールに基づき,数学者同士が難問を出し合う一種の試合が流行しており,数学者は見つけた事実をすぐに発表せず,次の試合に備えて多くの問題を予め解いて,秘密にしておくのが普通だったのです.フェロも,解法を秘密にしているうちに死んでしまったのだと考えられます.
現在,カルダノの公式と呼ばれている解法は,二コロ・フォンタナ(  )が発見したものです.フォンタナには吃音があったため,タルタリア (
)が発見したものです.フォンタナには吃音があったため,タルタリア ( 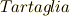 :吃音の意味)という通称で呼ばれており,現在でもこちらの名前の方が有名なようです.当時の慣習通り,フォンタナもこの解法を秘密にしていましたが,ミラノの数学者ジローラモ・カルダノ(
:吃音の意味)という通称で呼ばれており,現在でもこちらの名前の方が有名なようです.当時の慣習通り,フォンタナもこの解法を秘密にしていましたが,ミラノの数学者ジローラモ・カルダノ( 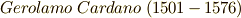 )に懇願され,他には公表しないという約束で,カルダノに解法を教えました.ところが,カルダノは
)に懇願され,他には公表しないという約束で,カルダノに解法を教えました.ところが,カルダノは 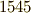 年に出版した
年に出版した 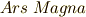 (ラテン語で"偉大な方法"の意味.いまでも 売ってます !)という書物の中で,まるで自分の手柄であるかのように,フォンタナの方法を開示してしまったため,以後,カルダノの方法と呼ばれるようになったのです. [*] フォンタナは抗議しましたが,後の祭りでした.
(ラテン語で"偉大な方法"の意味.いまでも 売ってます !)という書物の中で,まるで自分の手柄であるかのように,フォンタナの方法を開示してしまったため,以後,カルダノの方法と呼ばれるようになったのです. [*] フォンタナは抗議しましたが,後の祭りでした.
| [*] | フォンタナに敬意を表して,カルダノ=タルタリアの公式と呼ぶ場合もあります. |

ニコロ・フォンタナ(タルタリア)
カルダノの公式
式(1)からスタートします.

カルダノ(実はフォンタナ)の方法で秀逸なのは,ここで 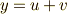 (ただし
(ただし 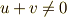 とする)と置換してみることです.すると,式(1)は次のように変形できます.
とする)と置換してみることです.すると,式(1)は次のように変形できます.
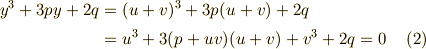
式(2)を成り立たせるには,次の二式が成り立てば良いことが判ります.

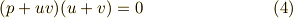
| [†] | 式 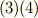 が成り立つことは,式 が成り立つことは,式 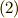 がなりたつための十分条件ですので, がなりたつための十分条件ですので, 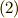 から から 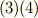 への変形が同値ではないことに気がついた人がいるかも知れません.これは への変形が同値ではないことに気がついた人がいるかも知れません.これは 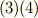 がなりたつことが がなりたつことが 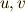 の定義だからで,逆に言えばそのような の定義だからで,逆に言えばそのような 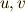 をこれから探したいのです.このような をこれから探したいのです.このような 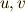 によって一般的に によって一般的に 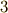 つの解が見つかりますが,三次方程式が3つの解を持つことは 代数学の基本定理 によって保証されますので,このような つの解が見つかりますが,三次方程式が3つの解を持つことは 代数学の基本定理 によって保証されますので,このような 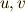 の置き方が後から承認される理屈になります. の置き方が後から承認される理屈になります. |
式(4)の条件は, 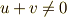 より,
より, 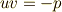 と書き直せます.この両辺を三乗して次式(6)を得ます.式(3)も,ちょっと移項してもう一度掲げます.
と書き直せます.この両辺を三乗して次式(6)を得ます.式(3)も,ちょっと移項してもう一度掲げます.


式(5)(6)を見て,何かピンと来るでしょうか?式(5)(6)は, 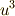 と
と 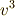 を解とする,次式で表わされる二次方程式の解と係数の関係を表していることに気がつけば,あと一歩です.(この二次方程式を,元の三次方程式の 分解方程式 と呼びます.)
を解とする,次式で表わされる二次方程式の解と係数の関係を表していることに気がつけば,あと一歩です.(この二次方程式を,元の三次方程式の 分解方程式 と呼びます.)

これを 二次方程式の解の公式 を用いて解けば,解として 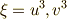 を得ます.
を得ます.
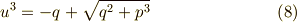
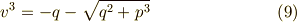
式(8)(9)を解くと,それぞれ三個の三乗根が出てきますが, 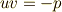 という条件を満たすものだけが式(1)の解として適当ですので,可能な
という条件を満たすものだけが式(1)の解として適当ですので,可能な 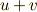 の組み合わせは三つに絞られます.
の組み合わせは三つに絞られます.
虚数が 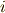 出てくる
出てくる
ここで,式(8)(9)を解く準備として,最も簡単な次の形の三次方程式を解いてみます.

これは因数分解可能で, 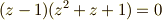 と変形することで,すぐに次の三つの解
と変形することで,すぐに次の三つの解 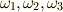 を得ます.
を得ます.
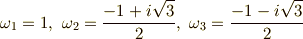
この  を使い,一般に
を使い,一般に 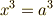 の解が,
の解が, 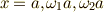 と表わされることを考えれば,式(8)の三乗根は次のように表わされます.
と表わされることを考えれば,式(8)の三乗根は次のように表わされます.
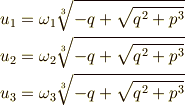
同様に,式(9)の三乗根も次のように表わされます.
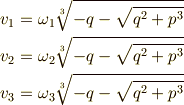
この中で, 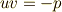 を満たす
を満たす 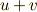 の組み合わせ
の組み合わせ 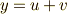 は次の三つだけです.
は次の三つだけです.
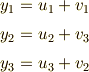
立体完成のところで 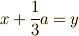 と置きましたので,改めて
と置きましたので,改めて 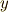 を
を  で書き換えると,三次方程式
で書き換えると,三次方程式 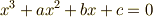 の解は次の三つだと言えます.これが,カルダノの公式による解です.
の解は次の三つだと言えます.これが,カルダノの公式による解です.
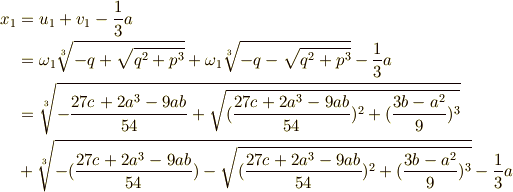
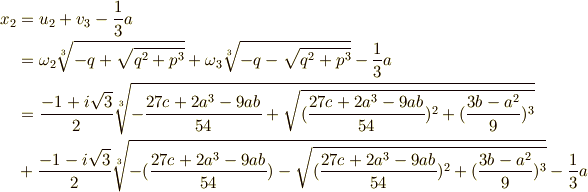
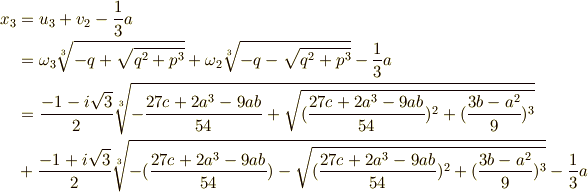
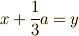 ,
, 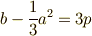 ,
, 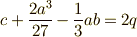
カルダノの公式の歴史2
二次方程式の解の公式が発見されてから,三次方程式の解の公式が発見されるまで数千年の時を要したことは意味深です.古代バビロニアの時代から, 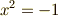 のような,虚数解を持つ二次方程式自体は知られていましたが,こうした方程式は単に『解なし』として片付けられて来ました.というのは,二乗してマイナス1になる数なんて,"実際に"存在しないからです.その後,カルダノの公式に至るまでの数千年間,誰一人として『二乗したらマイナス1になる数』を,仮にでも計算に導入することを思いつきませんでした.ところが,三次方程式の解の公式には,
のような,虚数解を持つ二次方程式自体は知られていましたが,こうした方程式は単に『解なし』として片付けられて来ました.というのは,二乗してマイナス1になる数なんて,"実際に"存在しないからです.その後,カルダノの公式に至るまでの数千年間,誰一人として『二乗したらマイナス1になる数』を,仮にでも計算に導入することを思いつきませんでした.ところが,三次方程式の解の公式には,  として複素数が出てきます.そして,例え三つの実数解を持つ三次方程式に対しても,公式通りに計算を進めていけば途中で複素数が顔を出します.ここで『二乗したらマイナス1になる数』を一時的に認めるという気持ち悪さを我慢して,何行か計算を進めれば,再び複素数は姿を消し,実数解に至るという訳です.
として複素数が出てきます.そして,例え三つの実数解を持つ三次方程式に対しても,公式通りに計算を進めていけば途中で複素数が顔を出します.ここで『二乗したらマイナス1になる数』を一時的に認めるという気持ち悪さを我慢して,何行か計算を進めれば,再び複素数は姿を消し,実数解に至るという訳です.
カルダノの公式の有用性ゆえに,架空の数としてであれ,人々は嫌々ながらもついに虚数を認めざるを得なくなりました.それでも,カルダノの著書では,まだ虚数を積極的に認めるには至っていません.カルダノは,解が実数解の場合には,途中で虚数を使わなくても済む公式が存在するのではないかと考え,そのような公式を見つけようと努力したようです.(現在では,解が実数解の場合でも,計算の途中に虚数が必要なことは証明されています.) むしろ虚数を認めて積極的に使っていこうという視点の転回を最初に行ったのは,アルベルト・ジラール(  )だと言われています.こうなるまでに,数千年の時間の要したことを考えると,抽象的概念に対する,人間の想像力の限界というものを考えさせられます.虚数が導入された後の数学の発展は,ご存知の通り目覚しいものがありました.
)だと言われています.こうなるまでに,数千年の時間の要したことを考えると,抽象的概念に対する,人間の想像力の限界というものを考えさせられます.虚数が導入された後の数学の発展は,ご存知の通り目覚しいものがありました.
| [‡] | 数学史上あまり重要ではないので脚注にしますが,カルダノの一生についても触れて置きます.カルダノは万能のルネッサンス人にふさわしく,数学者,医者,占星術師として活躍しました.カルダノにはギャンブルの癖があり,いつもお金に困っており,デカルトに先駆けて確率論の研究を始めました.また,機械的発明も多く,ジンバル,自在継ぎ手などは今日でも使われているものです.ただし,後半生は悲惨でした.フォンタナ(タルタリア)に訴えられ,係争に10年以上を要したほか,長男が夫人を毒殺した罪で処刑され,売春婦となった娘は梅毒で亡くなりました.ギャンブラーだった次男はカルダノのお金を盗み,さらにキリストのホロスコープを出版したことで,異端とみなされ,投獄の憂き目に遭い(この逮捕は次男の計画でした),この間に教授職も失いました.最後は,自分自身で占星術によって予め占っていた日に亡くなったということです. |
カルダノの公式の歴史3
カルダノは前出の自著  の中で四次方程式の解法をも紹介していますが,これは弟子のロドヴィーコ・フェラーリ(
の中で四次方程式の解法をも紹介していますが,これは弟子のロドヴィーコ・フェラーリ( 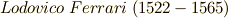 )が発見したものだと言われています.現代でも,人の成果を自分の手柄であるかのように発表してしまう人がいます.考えさせられる問題です.
)が発見したものだと言われています.現代でも,人の成果を自分の手柄であるかのように発表してしまう人がいます.考えさせられる問題です.
さて,カルダノの公式の発表以降,当然の流れとして五次以上の代数方程式に対しても解の公式を発見しようという試みが始まりましたが,これらの試みはどれも成功しませんでした.そして, 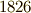 年,ノルウェーのニールス・アーベル(
年,ノルウェーのニールス・アーベル( 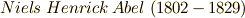 )により,五次以上の代数方程式には代数的な解の公式が存在しないことが証明されました.この証明はエヴァリスト・ガロア(
)により,五次以上の代数方程式には代数的な解の公式が存在しないことが証明されました.この証明はエヴァリスト・ガロア( 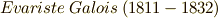 )によってガロア理論に発展させられ,群論,楕円曲線論など,現代数学で重要な位置を占める分野の出発点となりました.
)によってガロア理論に発展させられ,群論,楕円曲線論など,現代数学で重要な位置を占める分野の出発点となりました.

ノルウェーの切手にもなっているアーベル

わずか21歳で決闘に倒れた悲劇の天才・ガロア