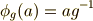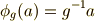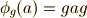群が集合の上で働くということ
群の元は,置換や回転など,何らかの『作用』を表わすものでした.そうした変換の集合である群に対し,いままでは群自身がどのような性質を満たすかという点にだけ注意を向けてきました.「演算について閉じている」「単位元がある」「逆元がある」等の話は,全て群自身の,つまり"群の構造"の話です.
しかし,群の元は『作用』ですから,実際に使ってみる場面では『作用を受ける対象』が何か必要です.この記事では,そのような対象に,群が働く働き方について勉強します.
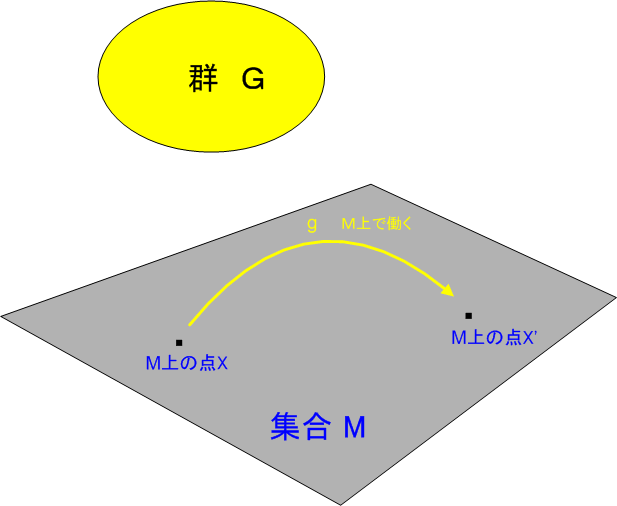
群の働く集合
群 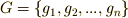 の元
の元 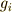 が,集合
が,集合  の元に作用するとします.つまり,元
の元に作用するとします.つまり,元 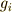 の引き起こす変換によって,
の引き起こす変換によって,  上の点が
上の点が  上の点に移されるということです(図では,点
上の点に移されるということです(図では,点  が
が 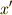 に移されることにしています.
に移されることにしています.  と
と 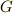 が別のものであることに注意してください).
が別のものであることに注意してください).
例えば,対称群  を考えてみましょう.このような順序の入れ替え操作自体は,抽象的なものです.しかし,この群が働きかける対象としては,例えば『正三角形の頂点
を考えてみましょう.このような順序の入れ替え操作自体は,抽象的なものです.しかし,この群が働きかける対象としては,例えば『正三角形の頂点 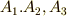 』『文字列
』『文字列  』『並んでいる3人の子供』などを考えることが出来ます.群と,群が働きかける集合とは,別の概念なのだという点をまずは理解して下さい.
』『並んでいる3人の子供』などを考えることが出来ます.群と,群が働きかける集合とは,別の概念なのだという点をまずは理解して下さい.
| [*] | いまのうちに,群と,群が上で働く集合とが,概念としては別のものだということをはっきりさせておいて下さい.そうしないと,いずれ『群が自分自身の上で働く』場合を勉強するときに頭が混乱してしまいます. |
| [†] | 対象となる集合は何でもよいのです.群の個々の元は何らかの作用を表わしていますので,群の被作用物となる集合が必要だ,というのがこの節のポイントです. |
これを 群Gが集合M上で働く と表現します.群の元の働きのことを,数学では 作用 と呼びます.群によって  上の点がどのような作用を受けるかを追跡して行くと,次の記事で勉強する,軌道という概念に至ります.
上の点がどのような作用を受けるかを追跡して行くと,次の記事で勉強する,軌道という概念に至ります.
群の働き方
群 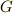 が働きかける集合
が働きかける集合  という概念が出てきましたが,では一体
という概念が出てきましたが,では一体 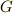 の元は,どのように
の元は,どのように  の元に作用するのでしょうか?そこで,どのような作用の仕方があるのかを見てみましょう.群
の元に作用するのでしょうか?そこで,どのような作用の仕方があるのかを見てみましょう.群 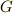 の元
の元 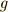 の,
の,  上の点に対する作用を関数とみて,一般に
上の点に対する作用を関数とみて,一般に 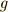 の作用を
の作用を 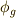 と表わすことにします.
と表わすことにします.
例5
例1,例2の方法と,逆元の方法を組み合わせた方法もあるでしょう.


他にも,色々な作用の仕方があるでしょう.結論から言えば,作用という言葉の意味を逸脱しない限り,どんな作用の仕方もあり得るのです.しかし,実用的な観点から,そして数学的な観点から興味があるのは,式番号を振っておいた三つのタイプ 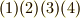 くらいです.これらには, 左からの作用
くらいです.これらには, 左からの作用  , 右からの作用
, 右からの作用 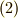 , 共役作用
, 共役作用 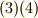 という名前が付いています.特に,これから先の議論では共役作用が大切です.
という名前が付いています.特に,これから先の議論では共役作用が大切です.
| [‡] | 群の元 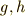 に対し,いままで元の結合を積の形で に対し,いままで元の結合を積の形で 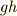 としてきましたが,この話と,元の作用の仕方(例えば としてきましたが,この話と,元の作用の仕方(例えば 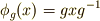 )を混乱している人がいるかも知れません.上の例では,元の作用は )を混乱している人がいるかも知れません.上の例では,元の作用は  上の点に対するもので,元同士の結合は 上の点に対するもので,元同士の結合は  上の点に働く,二つの関数の結合のように考えたら良いのです.元 上の点に働く,二つの関数の結合のように考えたら良いのです.元 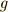 の作用 の作用  に に 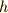 の作用を結合させれば, の作用を結合させれば, 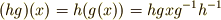 となります.群論の最初から,群の元の演算だとか結合法則だとかと言っていたのは,この左辺の となります.群論の最初から,群の元の演算だとか結合法則だとかと言っていたのは,この左辺の 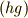 の部分のことだったんですね.作用の仕方(右辺)には色々あることをこの記事で見ましたが,どんな作用でも一般的に,作用は積の形で書けるのです.( 群について基本的なこと の乗群の項,三番目の脚注を参考にしてください.) まずは『群がある集合上で働く』ということと『元と元を結合する』という話が,概念的には別のものであることを納得して下さい.実はこのさき, の部分のことだったんですね.作用の仕方(右辺)には色々あることをこの記事で見ましたが,どんな作用でも一般的に,作用は積の形で書けるのです.( 群について基本的なこと の乗群の項,三番目の脚注を参考にしてください.) まずは『群がある集合上で働く』ということと『元と元を結合する』という話が,概念的には別のものであることを納得して下さい.実はこのさき,  として として 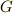 自身や 自身や 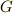 の部分集合を考える話題が出てきます.このほうが数学的には興味深いのですが,ここでしっかり理解しておかないと,頭が混乱してきてしまうと思います. の部分集合を考える話題が出てきます.このほうが数学的には興味深いのですが,ここでしっかり理解しておかないと,頭が混乱してきてしまうと思います. |
便利な働き方
なぜ,この三つの働き方が特に重要かというと,これらの作用の仕方は,次の三つの条件を満たすからです.これによって群 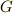 の構造と集合
の構造と集合  の作用の受け方に,ある程度の対応がつくことになります.
の作用の受け方に,ある程度の対応がつくことになります.
- 群
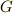 の元
の元 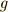 が,集合
が,集合  上の点を集合
上の点を集合  上の点に一対一に写像する.
上の点に一対一に写像する. - 群
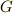 の単位元は,
の単位元は,  上の恒等変換に対応している.
上の恒等変換に対応している. - 群
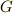 の逆元の関係にある二つの元
の逆元の関係にある二つの元 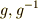 は,
は,  上で逆変換の関係にある二つの変換
上で逆変換の関係にある二つの変換 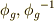 に対応している.
に対応している.
本当に,この三条件が満たされているかは, 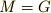 として,確認してみればすぐに分かります.
として,確認してみればすぐに分かります.
| [§] | 上に挙げた3つの条件がなりたてば,いかにも集合の取り扱いが楽になりそうなことは分かりますから,左作用・右作用・共役が大事なんだという所までは諒解できるかと思います.しかしこの3つの条件だけが問題ならば,左作用を考えるのが一番簡単に思えます.両側から,しかも片一方だけ逆元にして元を掛けるという,共役なんていう変チクリンな作用がどうして大事なのでしょうか?実は, 共役類 で改めて勉強しますが, 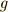 によって によって 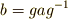 のように対応させられる二点 のように対応させられる二点 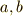 を同値だと考えることで,集合の元の間に同値関係を入れることができ,ここから共役作用を使って類別が出来るからです.今後,群論を学んでいく上で,共役作用がとても大事になります. を同値だと考えることで,集合の元の間に同値関係を入れることができ,ここから共役作用を使って類別が出来るからです.今後,群論を学んでいく上で,共役作用がとても大事になります. |
| [¶] | 共役作用だけでなく,他の作用を考えても同値関係は入れられます.一般に,群の元の作用 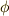 がよほど特殊なものでない限り,その作用による写像 がよほど特殊なものでない限り,その作用による写像 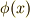 をもとの元 をもとの元  と同類とみなせば同値関係になるわけです.しかし共役作用の場合 と同類とみなせば同値関係になるわけです.しかし共役作用の場合  となり,このあと勉強する 正規部分群 と関係が深く,正規部分群となる部分群を作る操作と関係するために大事なのです. となり,このあと勉強する 正規部分群 と関係が深く,正規部分群となる部分群を作る操作と関係するために大事なのです. |
| [#] | 共役に二つの定義 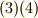 が出てきたのを,いぶかしく思っている人がいるかも知れません.どうせ が出てきたのを,いぶかしく思っている人がいるかも知れません.どうせ 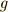 には逆元があるので, には逆元があるので, 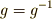 と置きなおせば同じことなのですが,気持ちとしては と置きなおせば同じことなのですが,気持ちとしては 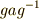 は左からの作用, は左からの作用, 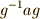 は右からの作用に従う定義になっています.もう少し詳しく説明しましょう.左からの作用は,結合則がなりたつことから,二つの左からの作用を連続させると は右からの作用に従う定義になっています.もう少し詳しく説明しましょう.左からの作用は,結合則がなりたつことから,二つの左からの作用を連続させると  のようになります.逆元に関しては のようになります.逆元に関しては 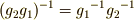 であることに注意すると, であることに注意すると, 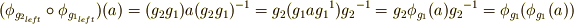 となり,確かに結合則が成り立ちます.逆に,右からの作用は連続して作用する場合, となり,確かに結合則が成り立ちます.逆に,右からの作用は連続して作用する場合,  , , 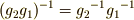 のように働きますから,同様にして のように働きますから,同様にして 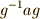 のように定義すると結合則を満たすのです.通常,よく用いるのは左からの作用に従った定義ですが,教科書によっては断りもなく右からの作用の形で書いてあるものもあり,『共役はどっちに のように定義すると結合則を満たすのです.通常,よく用いるのは左からの作用に従った定義ですが,教科書によっては断りもなく右からの作用の形で書いてあるものもあり,『共役はどっちに  が付くんだっけ?』と混乱する原因になります.一度,左作用と右作用の違いを理解しておけば,いつでもどちら側に が付くんだっけ?』と混乱する原因になります.一度,左作用と右作用の違いを理解しておけば,いつでもどちら側に  がつくのか自分で確認できるようになると思います.今後,特に断らない限り,主に左作用を使います. がつくのか自分で確認できるようになると思います.今後,特に断らない限り,主に左作用を使います. |
 とすると,次のように左から作用させるという方法が一つあります(これによって
とすると,次のように左から作用させるという方法が一つあります(これによって 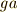 に移されます).
に移されます).