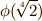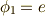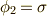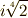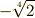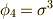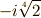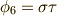ガロア群の例
ガロア群の定義はそれほど難しくありませんでしたが,ガロア群が具体的にどのような群であるか,すなわち,その元である自己同型写像がどのようなものであるかが,まだあまりピンと来ていないと思います.
実は,ガロア群の元は体によって簡単に決まる場合もあれば,なかなか求めるのが難しいような場合もあり,一般にはなかなか簡単に決まりません.特に,拡大次数が大きい場合には大変です.ガロア群を決定するための万能の方法はありませんが,幾つかの例と定理を見ながら,ガロア群に少しずつ慣れていきましょう.
まず,体の自己同型写像の定義を復習しましょう.
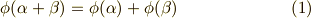

有理数体  を
を  に写す自己同型写像には,恒等写像しかないことが分かります.これは背理法ですぐに示せますが,もしも,ある有理数が違う有理数に写される場合があれば,式
に写す自己同型写像には,恒等写像しかないことが分かります.これは背理法ですぐに示せますが,もしも,ある有理数が違う有理数に写される場合があれば,式  が成り立たない反例をすぐに示せるからです.
が成り立たない反例をすぐに示せるからです.
Important
有理数体 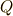 を
を 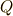 に移す自己同型写像には恒等写像しかありません.
に移す自己同型写像には恒等写像しかありません.
例1(二次拡大体)
最初に, 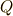 の二次拡大体の例として
の二次拡大体の例として 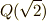 のガロア群
のガロア群 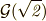 を考えます.
を考えます. 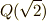 の元が全て
の元が全て 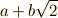 の形に書けるのはもう大丈夫だと思います.
の形に書けるのはもう大丈夫だと思います.
まず,明らかに恒等写像 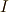 は自己同型写像で,
は自己同型写像で, 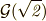 の元です.
の元です.
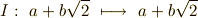
これは自明な元です.実は,もう一つそれほど明らかではない自己同型写像に, 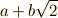 を
を 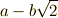 に写す写像があります.
に写す写像があります.
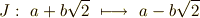
この写像 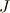 が確かに自己同型写像の定義を満たすことを確認してみましょう.式
が確かに自己同型写像の定義を満たすことを確認してみましょう.式 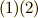 に
に 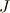 を代入してみます.
を代入してみます.
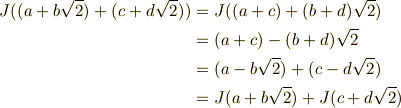
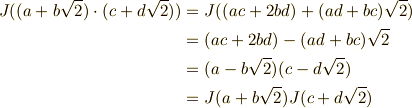
確かに 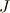 も自己同型写像の定義
も自己同型写像の定義 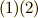 を満たすことが分かりました.
を満たすことが分かりました. 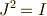 ですから,この自己同型写像群は
ですから,この自己同型写像群は 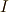 と
と 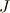 だけで閉じた位数
だけで閉じた位数 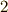 の群を作れます.
の群を作れます.
また, 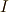 も
も 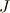 も
も 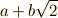 の形の元の有理数部分,つまりこの例の
の形の元の有理数部分,つまりこの例の  を不変に保ちますから,ガロア群
を不変に保ちますから,ガロア群  が分かります.
が分かります.
| [*] | のちほど,ガロア理論の応用として,定規とコンパスで作図可能な図形の問題や,代数方程式の可解性も問題を考えますが,そうした場合に二次拡大が非常に大事です. |
例2
もう一つ, 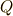 の拡大体
の拡大体 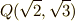 を考えてみましょう.
を考えてみましょう. 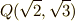 の元は,全て
の元は,全て 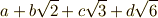 の形で表わすことができます.
の形で表わすことができます.
二つの 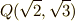 の元の積を考えて,恒等写像以外の自己同型写像の可能性を考えてみましょう.計算はけっこう大変です.
の元の積を考えて,恒等写像以外の自己同型写像の可能性を考えてみましょう.計算はけっこう大変です.
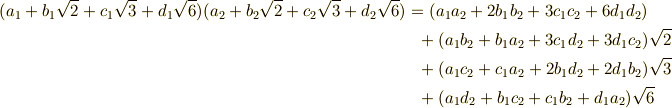
じっと両辺を見ていると,まず左辺の  と
と  の符号を
の符号を 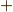 から
から  に変える写像
に変える写像  が,右辺でも二行目と四行目(つまり
が,右辺でも二行目と四行目(つまり  と
と  に相当)の符号だけを変えることが分かります.
に相当)の符号だけを変えることが分かります.
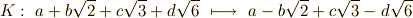
よって,  は式
は式 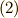 を満たしています.
を満たしています.  が式
が式  を満たすのは明らかですから,
を満たすのは明らかですから,  は
は 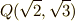 の自己同型写像になっています.同様に,
の自己同型写像になっています.同様に,  と
と  の符号だけを変える写像
の符号だけを変える写像 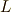 ,
,  と
と  の符号だけを変える写像
の符号だけを変える写像 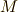 も自己同型写像になります.
も自己同型写像になります.
有理数の部分  を不変に保つ自己同型写像(つまり
を不変に保つ自己同型写像(つまり 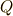 を固定体とする
を固定体とする 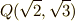 の自己同型写像)はこの四つだけですが,この四つの自己同型写像は確かに群をなします.群表は次のようになります.
の自己同型写像)はこの四つだけですが,この四つの自己同型写像は確かに群をなします.群表は次のようになります.
| I | K | L | M | |
|---|---|---|---|---|
| I | I | K | L | M |
| K | K | I | M | L |
| L | L | M | I | K |
| M | M | L | K | I |
これより,ガロア群 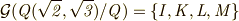 が分かります.この群が, クラインの四元群 と同型であることを,群表を比較して確認してください.ここで行った計算はやや面倒でしたが,自己同型写像を具体的に決めるには,定義式
が分かります.この群が, クラインの四元群 と同型であることを,群表を比較して確認してください.ここで行った計算はやや面倒でしたが,自己同型写像を具体的に決めるには,定義式 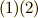 を満たすように地道に探すしかありません.
を満たすように地道に探すしかありません.
| [†] | 具体的に自己同型写像を探すしかないと書きましたが,たいていは例題のように,  の符号を入れ替える写像を考えれば良いです.複素共役を取る操作に似てますね. の符号を入れ替える写像を考えれば良いです.複素共役を取る操作に似てますね. |
補足
例2に出てきた 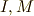 の二つは,
の二つは, 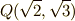 の元で
の元で 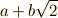 の部分の符号を変えませんので,
の部分の符号を変えませんので, 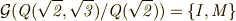 が言えます.このガロア群は,明らかに例1で見た
が言えます.このガロア群は,明らかに例1で見た  に同型です.
に同型です.
これは少し考えてみればもっともなことです.ガロア群は,二つの体の間にある,拡大の関係だけで決まってくる群ですので, 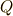 に
に 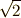 を添加した体と,
を添加した体と, 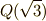 に
に 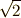 を添加した体とで,ガロア群
を添加した体とで,ガロア群  と
と 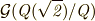 が同型になっていることに不思議はありません.このような関係を,よく次のような図で書く人もいます.図中,下の
が同型になっていることに不思議はありません.このような関係を,よく次のような図で書く人もいます.図中,下の 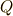 から上の
から上の 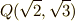 に到るのに,添加する元と中間体を示しているわけです.
に到るのに,添加する元と中間体を示しているわけです.

矢印の横には,ガロア群の元や位数など,追加情報を書き込みましょう.物理のかぎしっぽでは,このような図はあまり使わないと思いますが,演習問題を解く際に自分で考えるのには,きっと役に立つと思います.ここまでに 体の自己同型写像 で『ガロア拡大の拡大次数は,ガロア群の位数に等しい』という定理を導きましたが,例1と例2をもう一度振り返って,この関係を確認してみてください.
例3
有理数体 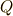 の拡大体
の拡大体 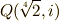 を考えてみます.
を考えてみます. 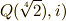 は,
は, 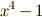 の解
の解 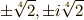 を
を 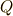 に添加して得られる体で,
に添加して得られる体で, 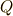 上
上 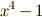 は既約ですから,
は既約ですから, 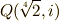 は
は 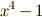 の最小分解体になっています.
の最小分解体になっています.
まずガロア群 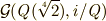 を求めてみましょう.
を求めてみましょう. 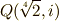 の元は一般に
の元は一般に 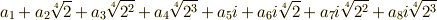 の形をしています.
の形をしています.
例題1,2と同じように考えますが, 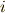 を基底とする項を
を基底とする項を  に変える写像は自己同型写像と言えます.同様に,
に変える写像は自己同型写像と言えます.同様に, 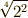 を
を 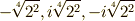 に変える写像も自己同型写像です.
に変える写像も自己同型写像です.
| [‡] | 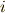 は二乗すると有理数, は二乗すると有理数, 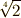 は四乗すると有理数になり,それぞれ は四乗すると有理数になり,それぞれ 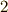 種と 種と 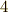 種の項で巡回的なループを作っています.そこで恒等写像も含めて 種の項で巡回的なループを作っています.そこで恒等写像も含めて 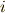 の項に の項に 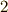 種, 種, 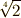 の項に の項に 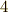 種の自己同型写像が考えられるわけです.次表に示すように, 種の自己同型写像が考えられるわけです.次表に示すように,  で計 で計 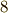 種になります.例題1,2よりも複雑ですね! 種になります.例題1,2よりも複雑ですね! |
これらの写像の組合わせは次表のようになります.  は適当につけた名前です.
は適当につけた名前です.
| 自己同型写像 | ||
|---|---|---|
ガロア群 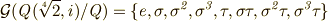 が得られました.
が得られました. 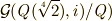 の位数と
の位数と 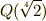 の拡大次数がどちらも
の拡大次数がどちらも 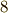 である点を確認してください.
である点を確認してください.
さて, 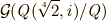 の元で,
の元で,  は
は 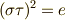 となりますので(確かめてください),
となりますので(確かめてください),  だけで位数
だけで位数 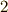 の部分群が作れます.また,
の部分群が作れます.また,  の固定体は,次のように実際に計算してみれば分かります.
の固定体は,次のように実際に計算してみれば分かります. 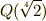 の元を
の元を 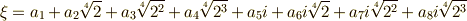 として,
として,  を作用させてみましょう.
を作用させてみましょう.
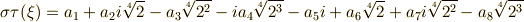
係数を見比べて, 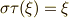 を満たすために
を満たすために 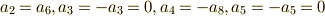 が要請されます.
が要請されます. 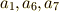 はこの変換によって不動です.これによって,
はこの変換によって不動です.これによって,  の固定体の元は次のような形であることが分かります.
の固定体の元は次のような形であることが分かります.

すこし技巧的ですが,これを次のように書き換えることも出来ます.
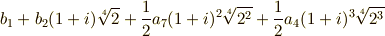
これより,  の固定体は
の固定体は 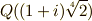 だと分かりました.
だと分かりました.
| [§] | ちなみに,  は は 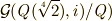 の正規部分群ではないため, の正規部分群ではないため, 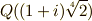 は は 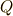 のガロア拡大ではありません. のガロア拡大ではありません. |