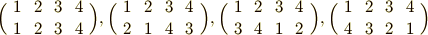クラインの四元群
教科書によく出てくるものに,クラインの四元群というものがあります.クラインの四元群とは,位数4の可換群です.位数4の可換群なので, 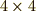 の群表(対角線に対して対称になるはず)を書けば,元同士の演算関係を網羅できるはずです.
の群表(対角線に対して対称になるはず)を書けば,元同士の演算関係を網羅できるはずです.
群の構造としては,群表を書いた時点で説明を尽くしているのですが,具体的にはクラインの四元群は  各軸回りに
各軸回りに 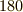 度回転させる回転操作の群として表現されます.
度回転させる回転操作の群として表現されます.
クラインの四元群
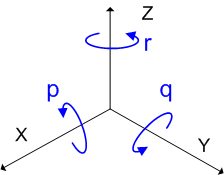
次図のように,  軸,
軸, 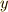 軸,
軸,  軸に沿って図形を
軸に沿って図形を 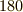 度回すような回転を,それぞれ
度回すような回転を,それぞれ 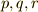 と名づけます.(有限回転の操作は,一般に非可換です. 無限小回転1 を参照してください.しかし,回転角が
と名づけます.(有限回転の操作は,一般に非可換です. 無限小回転1 を参照してください.しかし,回転角が 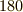 度の場合は可換になります.つまり,これは有限回転の操作の中では,かなり例外的なものです.)
度の場合は可換になります.つまり,これは有限回転の操作の中では,かなり例外的なものです.)
例えば,  の操作の後に続けて
の操作の後に続けて  の操作を行うことは,
の操作を行うことは,  の操作に等しくなります.
の操作に等しくなります.
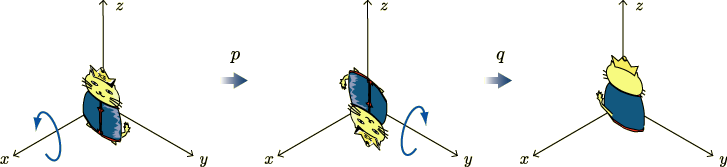
想像だけで考えていると混乱してくるので,どうか何か手に取って,実際に回して確認してみてください.同様に,  に続けて
に続けて  を行う変換は,
を行う変換は,  に等しくなります.また,同じ変換を二回続けて行うと,何もしなかったの(恒等変換
に等しくなります.また,同じ変換を二回続けて行うと,何もしなかったの(恒等変換  )と同じになります.
)と同じになります.
これらの回転操作 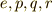 は群をなします.群表にまとめると,次のようになります.
は群をなします.群表にまとめると,次のようになります.
| e | p | q | r | |
|---|---|---|---|---|
| e | e | p | q | r |
| p | p | e | r | q |
| q | q | r | e | p |
| r | r | q | p | e |
| [*] | クラインの四元群の元 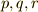 はどれも二乗すると はどれも二乗すると  になりますから位数は になりますから位数は 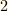 だと言えます.クラインの四元群は,巡回群ではない群としては最小のものです.クラインの四元群が存在することと,四次方程式に解の公式が存在することは,ガロア理論によって結び付けられます. だと言えます.クラインの四元群は,巡回群ではない群としては最小のものです.クラインの四元群が存在することと,四次方程式に解の公式が存在することは,ガロア理論によって結び付けられます. |
同じ構造の群
上の表中, 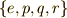 として,回転操作の代わりに,次のような四つの行列の積を考えても,上と同じ群表を満たします.計算して確かめてみましょう.ただし
として,回転操作の代わりに,次のような四つの行列の積を考えても,上と同じ群表を満たします.計算して確かめてみましょう.ただし 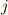 は二乗して
は二乗して 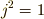 となる, 分離複素数 と呼ばれるちょっと変わった数です.複素数ではありません.
となる, 分離複素数 と呼ばれるちょっと変わった数です.複素数ではありません.
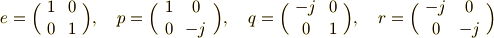
つまり,これらの行列の集合は,群として同じ構造をしているということです.他にもクラインの四元群と同じ構造の集合(元が4つあり,同じ群表を満たすもの)を探してみましょう.
| [†] | クライン(  )は,群論の幾何学における重要性を大いに研究した数学者です.クラインがエルランゲン大学で行った講義をまとめた『エルランゲン目録』は特に有名で,「一つの幾何学は,一つの変換群によって不変な性質を研究する不変式論である」との主張を行いました.なんのこっちゃ,と思うかも知れませんが,これはショッキングな宣言です.噛み砕いて言えば,あるタイプの幾何学には,一つの変換群が一対一に対応するという主張なのです.具体的には,ユークリッド幾何学には運動群が,アフィン幾何学にはアフィン群が,射影幾何学には射影変換群が対応するという具合です.このようにして,色々な分野に分かれていた幾何学が,群論によって統一的に扱われる可能性が拓かれ,逆に,群論の研究から,新しいタイプの幾何学が生まれてくる可能性もが示されました.いまや幾何学の勉強に群論は欠かせません. )は,群論の幾何学における重要性を大いに研究した数学者です.クラインがエルランゲン大学で行った講義をまとめた『エルランゲン目録』は特に有名で,「一つの幾何学は,一つの変換群によって不変な性質を研究する不変式論である」との主張を行いました.なんのこっちゃ,と思うかも知れませんが,これはショッキングな宣言です.噛み砕いて言えば,あるタイプの幾何学には,一つの変換群が一対一に対応するという主張なのです.具体的には,ユークリッド幾何学には運動群が,アフィン幾何学にはアフィン群が,射影幾何学には射影変換群が対応するという具合です.このようにして,色々な分野に分かれていた幾何学が,群論によって統一的に扱われる可能性が拓かれ,逆に,群論の研究から,新しいタイプの幾何学が生まれてくる可能性もが示されました.いまや幾何学の勉強に群論は欠かせません. |
練習問題2
二つの文字からなる集合 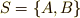 と
と 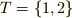 を考えます.これらを組み合わせできる文字は全部で
を考えます.これらを組み合わせできる文字は全部で 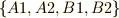 の4つです.これに二つの関数
の4つです.これに二つの関数 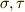 を考えます.
を考えます.  は文字に作用すると
は文字に作用すると 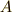 と
と 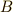 を入れ換えてしまう関数です.すなわち
を入れ換えてしまう関数です.すなわち 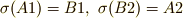 のようになります.一方,
のようになります.一方,  は数字を入れ換えてしまう関数で
は数字を入れ換えてしまう関数で 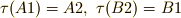 のように働きます.
のように働きます.
 と
と  の結合は可換であることを確認してください.
の結合は可換であることを確認してください.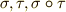 と恒等置換
と恒等置換  の四つは群をなし,クラインの四元群と同型であることを確認してください.
の四つは群をなし,クラインの四元群と同型であることを確認してください.
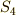 の元のうち, 次の四つを元とする部分群だと言うこともできます.群表を書いて確認してみましょう.(上の群表で
の元のうち, 次の四つを元とする部分群だと言うこともできます.群表を書いて確認してみましょう.(上の群表で