渦度ベクトルと循環

ベクトル場 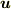\bm{u} が流れ場を意味するとき，次式で定義されるベクトルを 渦度ベクトル と呼びます．

\bm{\omega} = \nabla \times \bm{u} \tag{1}

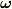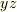渦度ベクトルの各座標成分は，座標軸に直交する平面内の渦度を表わしています．（例えば， \bm{\omega} の x 成分は yz 平面内の渦度を表わします． rot を参照して下さい．）また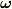， \bm{\omega} の流線を 渦線 と呼び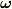， \bm{\omega} の流管を 渦管 と呼びます．渦線の方程式は次のように与えられます．

\frac{dx}{\omega_{1}} = \frac{dy}{\omega_{2}} = \frac{dz}{\omega_{3}} \tag{2}

渦糸は，渦管の無限に細いものだと考えることも出来ます．粘性抵抗の働かない流体（完全流体と呼びます）においては，渦は消えたり生まれたりしないことが知られており， 渦は不生不滅 などと言われます．

[*]この定理は，ラグランジェの定理，ケルビンの定理，ヘルムホルツの定理などとも呼ばれます．これらの定理は，多少表現が異なりますが，結局，渦の不生・不滅を主張するものです．ここではあまり詳しい説明はしませんので，興味のある人は流体力学の教科書を参考にしてみて下さい．

循環

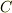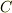流れ場の中のある閉曲線 C に沿って， C の接線速度を周回積分したものを 循環 と呼びます．循環は，ストークスの定理を用いると，渦度ベクトルの面積分に直すことも出来ます．

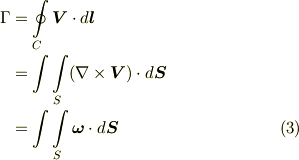
\Gamma &= \ointop \limits _{C} \bm{V} \cdot d\bm{l } \\&= \int \int \limits _{S} (\nabla \times \bm{V}) \cdot d\bm{S} \\ &= \int \int \limits _{S} \bm{\omega} \cdot d\bm{S} \tag{3}

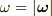三行目で，任意に渦管を取るとき，その断面で循環の大きさは常に同じだということが言えます．（流管の断面を単位時間当たりに過ぎる流量が一定であることと，基本的には同じ理屈です． ベクトル場の流束と流管 を参照して下さい．）特に，渦糸は断面積が無限に小さい渦管と見なせますので，その断面の曲率を無視して断面積を {\sigma} とし， \omega = |\bm{\omega}| とすると次式が成り立ちます．

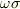\Gamma = \omega \sigma \tag{4}

この \omega \sigma を 渦糸の強さ と呼びます．渦や渦糸の話題は尽きませんが， 詳しくは流体力学の解説を見て下さい．この記事は，ベクトルの回転，ストークスの定理，流線，流管といった概念の応用例として，渦と循環をほんの少しだけ取り上げてみました．（いずれ，流体力学の記事もきちんと書くかも知れません．）