ベクトルの関数

いままでに出てきたベクトルは，主に大きさの変わらないベクトルでした．大きさが一定のベクトルを 定ベクトル と呼びます．この記事以降では，ベクトルが関数になっており，大きさや向きをダイナミックに変える場合を考えます．

関数の変化を考えるには，当然，微積分が関係してきます．ここからはベクトルを微分したり積分したりする話題を勉強します．普通の関数の微積分が分かっている人にとって，ベクトルの微積分だからと言って技術的に難しいことは特にありませんが，ベクトルならではの面白い話題が幾つもあります．これから勉強する内容を，だいたい俯瞰してみましょう．

ベクトルの関数

まず，ベクトル 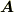$\bm{A}$ が，何かスカラーのパラメーター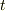の関数になっている場合が考えられます．

$\bm{A} = \bm{A} (t) \tag{1}$

つまり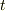，が変化すると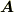， $\bm{A}$ の向きや大きさを変わるということです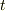．は時間とは限りませんが，物理的なイメージとしては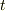，を時間だと考えても良いでしょう．そうすると，時々刻々その大きさや向きを変えるベクトル，例えばある場所で観測している風力がこの形で表わせそうです．風の向きと強さを計測できる装置でデータを取ってみると，風力と風向は時々刻々変わることでしょう．

次のタイプとして，ベクトルがベクトルの関数になっている場合があります．

$\bm{A} = \bm{A} (\bm{x}) \tag{2}$

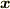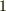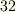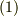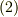やはり理解の為に具体的にイメージしてみましょう． $\bm{x}$ を位置ベクトルと考え，ふたたび風を例に取れば分かりやすいと思います．ある時間における風力と風向は，場所によって異なります．例えば，今日の午後時分に，東京では南向きの微風が吹いていたとしても，スコットランドでは北向きの強風が吹いていたかも知れません．このように，ベクトルがベクトルの関数になっているものもなかなか重要そうですね．本当は，風は時間と場所によって変わりますから，式 (1) と (2) を合わせて次のように書くと万能です．

$\bm{A} = \bm{A} (t, \bm{x}) \tag{3}$

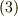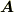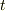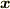流体力学では，一般に水や空気の流れを式 (3) の形で表わします．ベクトル $\bm{A}$ が，スカラーとベクトル $\bm{x}$ 両方の関数になっています．このように，変数にスカラーとベクトルが混ざっているようなものもあります．逆に，変数がベクトルになっていて，関数値のほうはスカラーというものもあるでしょう．

$f= f(\bm{x} ) \tag{4}$

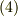式 (4) の形の例として思いつくのは，大気中の温度です．温度はスカラー値ですが，場所によって異なりますから，位置ベクトルの関数となるはずです．式 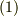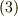(1) 〜 (3) はベクトルが関数になっているという意味で ベクトル関数 と呼んだりしますが，とくに『関数の値がベクトルである』という点を強調して ベクトル値関数 と呼ぶこともあります．テンソルを勉強した人は，スカラーもベクトルもテンソルの一種だということを知っていると思いますが，実は，式 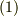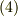(1) 〜 (4) は全て，テンソル関数の特殊な場合だと言うことが出来ます．

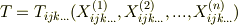
$T=T_{ijk...}(X_{ijk...}^{(1)},X_{ijk...}^{(2)},...,X_{ijk...}^{(n)})$

ベクトルの微積分をして面白いこと

流体力学や電磁気学など，流れを扱う分野（電場や磁場も流れ場と考えられます）では，流れを微積分する計算が重要です．こうしたベクトルの微積分から，保存量やポテンシャルなどの便利な概念を導くことができますので，ベクトル値関数の計算がとても重要です．しかし，ベクトルを微積分して嬉しいのは，このような応用的な意味合いからだけではありません．

例えば，偏微分記号 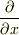$\frac{\partial }{\partial x}$ を組み合わせてつくった 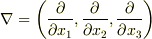$\nabla = \left( \frac{\partial }{\partial x_{1}},\frac{\partial }{\partial x_{2}},\frac{\partial }{\partial x_{3}} \right)$ というベクトルが登場します．これは微分演算子を成分とするベクトルだという意味で，普通のベクトルとは少し違うものですが（ベクトル演算子と呼ばれます），形式的には，既にお馴染みの 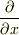$\frac{\partial }{\partial x}$ という記号を組み合わせてベクトルを作ってみただけのように見えます．

しかし，面白いことに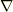， $\nabla$ は座標系にはよらない式を作ります．例えば，次の方程式が何か物理的な方程式だとすると，これは座標系の取り方には依存しない表現になります．

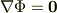
$\nabla \Phi = \bm{0}$

[*]

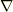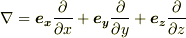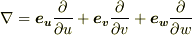座標系の取り方によらないことが，座標変換に対して不変なことを意味する訳ではありません． $\nabla$ という記号には座標系の情報が入っていないので，これを $\nabla = \bm{e_{x}}\frac{\partial}{\partial x}+ \bm{e_{y}}\frac{\partial}{\partial y}+ \bm{e_{z}}\frac{\partial}{\partial z}$ と書いても，別の座標系で $\nabla = \bm{e_{u}}\frac{\partial}{\partial u}+ \bm{e_{v}}\frac{\partial}{\partial v}+ \bm{e_{w}}\frac{\partial}{\partial w}$ と表現しても良いわけで，これが座標系の取り方によらないという意味です．座標変換に対して不変と言うと，まるで $\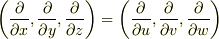left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right) = \left( \frac{\partial}{\partial u}, \frac{\partial}{\partial v}, \frac{\partial}{\partial w} \right)$ が成り立っているかのように聞こえますが，そんなことはありません．言葉の意味に注意して下さい．

『ベクトルの成分は一般的に座標系の取り方による』という点は，これまでも繰り返し触れてきました．このことを考えると，どうやら 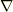$\nabla$ の出て来るベクトル解析は，単にベクトルを微積分するというだけではなく，何か，座標系に関係しない普遍的な表現にも関係した深みのある分野のように思えてきます．ベクトル解析分野では，ガウスの発散定理，グリーンの定理，ストークスの定理と呼ばれる積分の定理を紹介する予定ですが，座標系によらない表現をつきつめ，微分形式という理論に行き着くと，実はこれらが単一の定理から出て来ることが見えてきます．電磁気学や流体力学への応用にも随時触れる予定ですが，せっかくなので，ベクトル解析から始めて，美しい微分形式の理論にもつながるように勉強していきたいと思います．

[†]	物理のかぎしっぽベクトル解析分野では，最初から共変ベクトルと反変ベクトルの違い明示的に示してベクトル代数，テンソル代数の議論を進めてきました．とりあえず，このベクトル解析というカテゴリーでは，初歩的な応用性を考え，特に断りの無い限り，ほとんどの内容は直交座標系で考えるものとします．テンソル解析のカテゴリーで，再び双対空間の話などに戻ると思います．

[home] [ベクトル解析] [ページの先頭]