ベクトルの割り算
ベクトルには割り算が定義されていません.なぜ割り算を定義できないかを一度自分でよく考えてみると,内積や外積の良い復習になると思います.
割り算は掛け算の逆演算ですから,掛け算(つまり内積と外積)の計算を逆に行えるかを検討していきます.
内積
まず内積の計算, 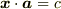 を考えてみます.
を考えてみます. 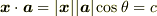 と書けますので,図形的な内積の意味は『
と書けますので,図形的な内積の意味は『 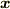 を
を 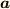 に射影した長さと,
に射影した長さと, 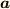 の絶対値の積』です.
の絶対値の積』です.

ところが, 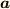 に射影した長さが,図の
に射影した長さが,図の 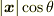 に等しくなるベクトルは,幾らでもあります.
に等しくなるベクトルは,幾らでもあります.
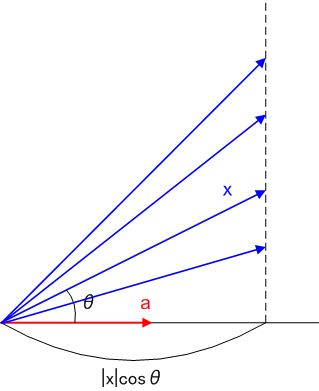
そういうわけで, 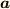 と
と  を決めても,
を決めても, 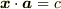 を満たす
を満たす 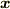 は幾らでもあることになり,一意的に
は幾らでもあることになり,一意的に 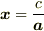 という計算はできないわけです.
という計算はできないわけです.
割り算が定義できませんので,つぎのような計算は 間違い です.

外積
次にベクトルの外積を考えてみましょう.外積 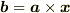 はベクトルで,向きは右手系では次図のような向き,大きさ
はベクトルで,向きは右手系では次図のような向き,大きさ 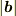 は
は 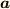 と
と 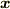 の張る平行四辺形の面積に等しいものと定義されています.
の張る平行四辺形の面積に等しいものと定義されています.
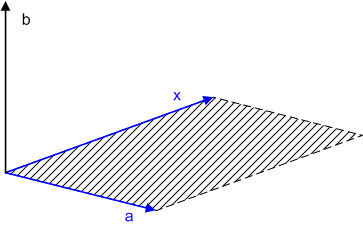
ところが,同じ面積の平行四辺形を張る 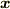 は幾らでもあります.向きと大きさという観点だけで言えば,次図の『赤い
は幾らでもあります.向きと大きさという観点だけで言えば,次図の『赤い 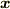 』と『青い
』と『青い 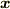 』とで,外積
』とで,外積 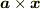 は同じになります.
は同じになります.
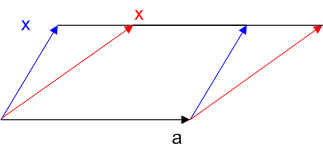
そういうわけで,外積に関しても一意的に商 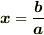 を決めることは出来ないようです.
を決めることは出来ないようです.
(発展)代数的な見方
実際にベクトルの割り算ができなくて不便を感じるという場面は少ないと思いますが,割り算ができないとはどういうことなのか,少し数学的に考えてみましょう.代数学の立場で考えてみると,ベクトルの加法には減法という逆演算があるので,ベクトル全体の集合は群(加群)になりそうだと考えられます.しかし,外積をベクトル同士の乗法とすれば,外積には逆演算がないので,乗群にはなりません.
| [*] | スカラー積(ベクトルをスカラー倍する演算)には逆元がありますが,スカラーはベクトルではないのですし,内積は結果がスカラーになってしまいますから,どちらも『ベクトルだけの集合を考えたときの内部演算』としては不適切です. |
加法と乗法の両方に逆演算が定義されていませんので,『ベクトル全体の集合』は 体 にはなりません.しかし, 環 にはなります.特に,外積は非可換ですので,これは 非可換環 です.なんだか難しそうな名前です.
ベクトル全体からなる集合の代数的構造を抽象化したのが, ベクトル空間 とよばれる概念です.本格的な代数系の教科書では,ベクトル空間を「体上の加群」という章で扱うことが多いようです.
代数学を勉強したことのある人は,せっかくなので,こんな風に代数系としてのベクトルの位置づけを整理しておくと視野が広がると思います.代数学を勉強したことのない人は,今からでも遅くありません!! こちら へどうぞ.