三重積
二つのベクトルの掛け算には 内積  と 外積
と 外積  という二種類がありました.内積はスカラーに,外積はベクトルになりますから,これらを スカラー積 , ベクトル積 と呼ぶこともあります.
という二種類がありました.内積はスカラーに,外積はベクトルになりますから,これらを スカラー積 , ベクトル積 と呼ぶこともあります.

この記事ではさらに, 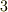 つのベクトルの積を考えます.ベクトルを
つのベクトルの積を考えます.ベクトルを 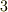 つ掛けると言っても,内積と外積の組み合わせに色々ありそうです.
つ掛けると言っても,内積と外積の組み合わせに色々ありそうです.



式 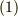 で定義される三重積は
で定義される三重積は 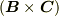 の部分がベクトルで,それと
の部分がベクトルで,それと 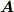 の内積を取るのですから,結果はスカラーになります.これを スカラー三重積 と呼びます.
の内積を取るのですから,結果はスカラーになります.これを スカラー三重積 と呼びます.
式 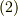 で定義される三重積は
で定義される三重積は 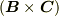 部分のベクトルと,ベクトル
部分のベクトルと,ベクトル 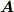 の更に外積を取りますので,結果もベクトルになります.これを ベクトル三重積 と呼びます.
の更に外積を取りますので,結果もベクトルになります.これを ベクトル三重積 と呼びます.
式 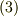 は,
は, 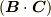 の部分がスカラーですから,ベクトル
の部分がスカラーですから,ベクトル 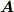 を単にスカラー倍しているだけで面白くもなんともない計算です.もちろん
を単にスカラー倍しているだけで面白くもなんともない計算です.もちろん 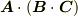 や
や 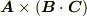 は定義不能です.
は定義不能です.
結局,なんだか面白そうなのは,スカラー三重積とベクトル三重積の二つです.
スカラー三重積
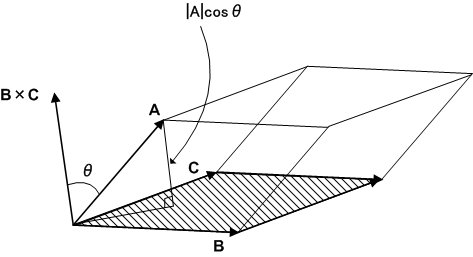
まず,ベクトル 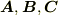 は一次独立だとします.外積の定義より,
は一次独立だとします.外積の定義より, 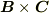 は,長さがベクトル
は,長さがベクトル 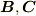 の張る平行四辺形の面積に等しく,向きは平行四辺形の法線方向を向いたベクトルです.(次図参照.外積の向きは右手系に取っています.)
の張る平行四辺形の面積に等しく,向きは平行四辺形の法線方向を向いたベクトルです.(次図参照.外積の向きは右手系に取っています.)
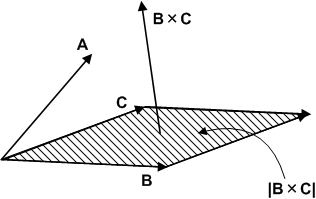
このベクトルと 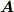 の内積を取ります.
の内積を取ります.
ここに出てくる  は,
は, 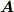 と
と 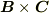 がなす角度です.ところで,次図のように
がなす角度です.ところで,次図のように 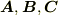 の張る平行六面体を考えると,
の張る平行六面体を考えると, 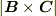 は底面積,
は底面積, 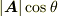 は高さになっていますから,スカラー三重積は
は高さになっていますから,スカラー三重積は 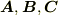 の張る 平行六面体の体積になる ことが分かります.
の張る 平行六面体の体積になる ことが分かります.
図形的意味からも明らかですが,スカラー三重積は積の順番によりません.
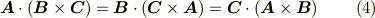
また,ベクトル 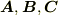 が一次従属の場合,平行六面体はつぶれてしまいますから,その体積は零で,スカラー三重積は
が一次従属の場合,平行六面体はつぶれてしまいますから,その体積は零で,スカラー三重積は 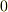 になります.もちろん,
になります.もちろん, 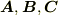 の中に同じベクトルがある場合もスカラー三重積は
の中に同じベクトルがある場合もスカラー三重積は 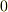 になります.
になります.
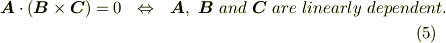
スカラー三重積を,次のように行列式で表現することもできます.

公式 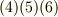 は,実際に成分を代入すれば簡単に証明できますので,ここでは証明は省略しますが,ぜひ一度自分で確認してみて下さい.
は,実際に成分を代入すれば簡単に証明できますので,ここでは証明は省略しますが,ぜひ一度自分で確認してみて下さい.
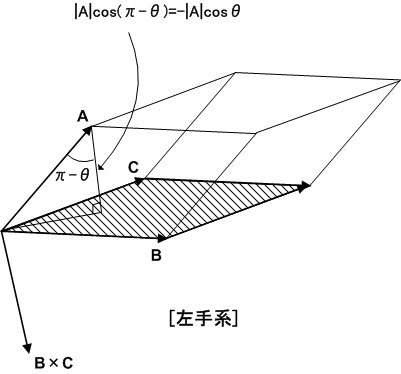
もう一つ重要なことがあります.それは,スカラー三重積は平行六面体の 向きつき体積 を表わしているという点です. 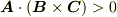 ならば,
ならば, 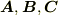 は右手系,
は右手系, 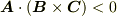 ならば,
ならば, 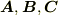 は左手系の基底になります.このことは,先ほどの図に示した
は左手系の基底になります.このことは,先ほどの図に示した 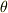 が,左手系の場合には
が,左手系の場合には 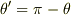 になるため,
になるため, 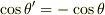 になると考えれば納得いくと思います.( 軸性ベクトルと極性ベクトル を参照してください.)
になると考えれば納得いくと思います.( 軸性ベクトルと極性ベクトル を参照してください.)
三つのベクトルさえあれば,順番は関係ないということでしたので,ベクトル三重積を括弧を使って次のように書くこともあります.
![[\bm{A} \bm{B} \bm{C}]=\bm{A} \cdot (\bm{B} \times \bm{C}) = \bm{B} \cdot (\bm{C} \times \bm{A}) = \bm{C} \cdot (\bm{A} \times \bm{B})](./f84157056ae8b456bb831ed16b1940d4.png)
この括弧を グラスマン記号 と呼びます.スカラー三重積をしょっちゅう使う人には便利な表記法でしょう.
| [*] | グラスマン(    )の父は数学と物理の教師でしたが,グラスマンの学校の成績は芳しくなく,両親からは職人か庭師になるのが良いと思われていました.徐々に成績を上げ,大学に進んだグラスマンでしたが,大学では神学,哲学,古典などを勉強し,数学や物理には無縁でした.大学卒業後,ようやく数学に興味が向き始め,独学を続けながらギムナジウム(ドイツの中学・高校に相当)の教師になりましたが,教員試験の成績も芳しくなく,レベルの低いクラス専門の教師として働き始めました.より上級の教員試験に挑戦しつつ数学の研究も続けたグラスマンは, )の父は数学と物理の教師でしたが,グラスマンの学校の成績は芳しくなく,両親からは職人か庭師になるのが良いと思われていました.徐々に成績を上げ,大学に進んだグラスマンでしたが,大学では神学,哲学,古典などを勉強し,数学や物理には無縁でした.大学卒業後,ようやく数学に興味が向き始め,独学を続けながらギムナジウム(ドイツの中学・高校に相当)の教師になりましたが,教員試験の成績も芳しくなく,レベルの低いクラス専門の教師として働き始めました.より上級の教員試験に挑戦しつつ数学の研究も続けたグラスマンは, 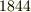 年, 年, 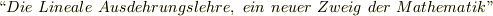 (線形拡大論,数学の新しい分野)という,ベクトルの理論と外積代数に関する画期的な著作を発表しましたが,非常に抽象的で難解なため,当初は研究の重要性があまり理解されなかったようです.例えば,メビウス( (線形拡大論,数学の新しい分野)という,ベクトルの理論と外積代数に関する画期的な著作を発表しましたが,非常に抽象的で難解なため,当初は研究の重要性があまり理解されなかったようです.例えば,メビウス(    )は,この本の重要性を理解せず,序文を書くのを断っています.その後ギブス( )は,この本の重要性を理解せず,序文を書くのを断っています.その後ギブス(  )等により主に電磁気学の文脈でベクトルの理論が発展させられ,ようやくグラスマンの仕事の重要性と先見性が広く認められるようになりました. )等により主に電磁気学の文脈でベクトルの理論が発展させられ,ようやくグラスマンの仕事の重要性と先見性が広く認められるようになりました. |
ベクトル三重積
ベクトル三重積 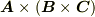 は次のように表わされます.
は次のように表わされます.
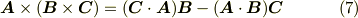
この公式の証明は,実際に成分を代入すれば示せるのでここでは省略します.外積の定義より, 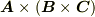 は
は 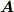 に直交するはずです.また,
に直交するはずです.また, 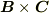 は
は 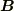 と
と 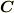 の張る平面に垂直な向きですが,
の張る平面に垂直な向きですが, 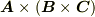 は
は 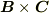 とも垂直な向きなので,結局
とも垂直な向きなので,結局 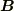 と
と 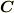 の張る平面に乗るベクトルとなります.
の張る平面に乗るベクトルとなります.
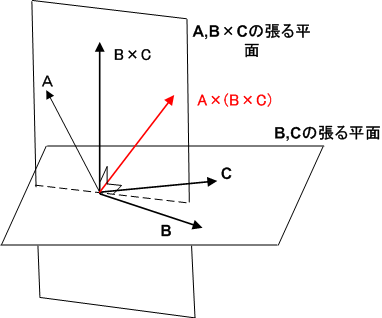
ベクトル三重積は,スカラー三重積とは異なり,ベクトルを入れ替えたら結果が変わってきます.式  の
の 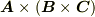 を巡回的に入れ替えることで,他の組み合わせの場合の公式を簡単に得ることができます.
を巡回的に入れ替えることで,他の組み合わせの場合の公式を簡単に得ることができます.
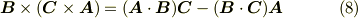
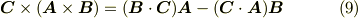
式 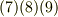 を足し合わせると次式を得ます.これは三つのベクトルについて,いつでも成り立つ恒等式です.
を足し合わせると次式を得ます.これは三つのベクトルについて,いつでも成り立つ恒等式です.
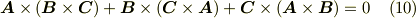
これを ヤコビの恒等式 と呼ぶことがあります.とても美しい結果ですね.
| [†] | 一般に,二種類の元 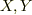 の積(どんな掛け算かは問わない)を, の積(どんな掛け算かは問わない)を, ![[X,Y]=XY-YX](./912ce7b464de625c20541103570238fc.png) と定義したものを交換子積,もしくはブラケット積と呼び,このような演算の入ったベクトル空間をリー代数と呼びます.交換子積は と定義したものを交換子積,もしくはブラケット積と呼び,このような演算の入ったベクトル空間をリー代数と呼びます.交換子積は ![[X,Y]=-[Y,X]](./e0196c084efdf008a58d437c545c6e23.png) を満たしますので,符号について反対称的だと言われます.また交換子積には一般に を満たしますので,符号について反対称的だと言われます.また交換子積には一般に ![[X,[Y,Z]]+[Y,[Z,X]]+[Z,[X,Y]]=0](./1d54345d4a87067d84e2de1783ed3f60.png) が成り立ち,これを一般にヤコビの恒等式と呼びます.式 が成り立ち,これを一般にヤコビの恒等式と呼びます.式 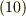 は,三次元ユークリッド空間 は,三次元ユークリッド空間 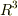 に私達の知っているベクトルの加法と外積を入れると,リー代数になるという主張とも解釈できるわけです.ここではリー代数の話題にこれ以上深入りしませんが,背後にはそんな話題が伏線にあったのだということを何となく知っておくと,そのうち役にたつかも知れません. に私達の知っているベクトルの加法と外積を入れると,リー代数になるという主張とも解釈できるわけです.ここではリー代数の話題にこれ以上深入りしませんが,背後にはそんな話題が伏線にあったのだということを何となく知っておくと,そのうち役にたつかも知れません. |