ベクトルからテンソルを作る
二つのベクトル成分 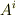 と
と 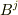 があるとき,この成分を掛け合わせたものは二階のテンソル成分になります.
があるとき,この成分を掛け合わせたものは二階のテンソル成分になります.
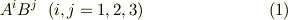
本当に二階のテンソルになるのかどうか,定義に戻って確認してみましょう. 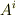 と
と 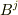 はベクトルですから,適当な二階のテンソル
はベクトルですから,適当な二階のテンソル 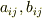 に対し,次の変換式を満たすはずです.
に対し,次の変換式を満たすはずです.


これは テンソルの概念 に出てきた,テンソルの定義式です.ベクトルは一階のテンソルですから,式 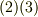 をベクトルの定義式だと考えても良いでしょう.
をベクトルの定義式だと考えても良いでしょう.
式 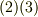 の両辺を掛け合わせて次式を得ます.
の両辺を掛け合わせて次式を得ます.
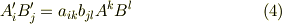
これは二階のテンソルの座標変換の式そのものですから, 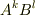 は二階のテンソルだと言えます.
は二階のテンソルだと言えます.
同様に,三つのベクトル成分の積 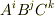 は三階のテンソル,四つのベクトル成分の積
は三階のテンソル,四つのベクトル成分の積 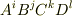 は四階のテンソルになります.
は四階のテンソルになります.
| [*] | いま反変テンソル 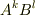 が共変テンソル が共変テンソル 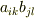 によって共変テンソル によって共変テンソル 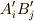 に移される例で考えましたが,共変・反変の組合わせは本質的にはそれほど重要ではありません. テンソルの概念 の式 に移される例で考えましたが,共変・反変の組合わせは本質的にはそれほど重要ではありません. テンソルの概念 の式  を参照して下さい. を参照して下さい. |
基底で考えてみる
ベクトルの成分の積がテンソルになるという事情を,もう少し探ってみます.ベクトル 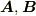 は基底を明示的に書けば次のように表現できました.
は基底を明示的に書けば次のように表現できました.
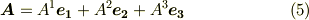
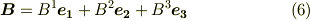
いま,式 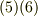 の両辺を掛け合わせることにします.成分は実数ですから普通に掛け算することにして,基底と基底の積にはテンソル積を使います.
の両辺を掛け合わせることにします.成分は実数ですから普通に掛け算することにして,基底と基底の積にはテンソル積を使います.
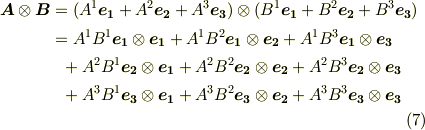
式 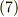 の一行目から二行目への変形は,普通に分配法則を使って一項ずつ展開しただけです.すでに テンソルの概念 で触れたように,これは
の一行目から二行目への変形は,普通に分配法則を使って一項ずつ展開しただけです.すでに テンソルの概念 で触れたように,これは 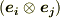 を基底とする二階のテンソルになっています.前セクションの議論は,このベクトルのテンソル積
を基底とする二階のテンソルになっています.前セクションの議論は,このベクトルのテンソル積  が,テンソルの変換則
が,テンソルの変換則 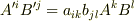 を満たすことを保証するものです.
を満たすことを保証するものです.
逆に『全ての  階のテンソルは
階のテンソルは  個のベクトルの積として表わせる』ことを証明することも出来ます.これによって,変換則
個のベクトルの積として表わせる』ことを証明することも出来ます.これによって,変換則 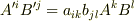 による定義と,ベクトルのテンソル積
による定義と,ベクトルのテンソル積 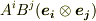 としての定義とが完全に同値であることが保証されます.さらに, テンソルの概念 で
としての定義とが完全に同値であることが保証されます.さらに, テンソルの概念 で 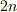 階のテンソル
階のテンソル  を
を 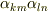 のように
のように 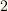 階テンソルの積に分解して書きましたが,この分解が常に可能であることも保証されます.
階テンソルの積に分解して書きましたが,この分解が常に可能であることも保証されます.
theorem
 階テンソルは,ベクトルの
階テンソルは,ベクトルの  個のテンソル積に分解できます.
個のテンソル積に分解できます.
この証明は少し面倒なので,特に二階のテンソルが二つのベクトルの積に分解できることだけを示します.それでもかなり面倒ですので,あまり細かい証明に拘らない人は結果だけを了承して先に進んでも構わないと思います.一般の階数のテンソルへの拡張は,帰納法を使えば容易です.証明の中で,ベクトルは太字体,ベクトル成分は細字体であることに注意してください.
proof
正規直交基底  を考えます.二階のテンソル
を考えます.二階のテンソル 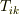 を何らかのベクトルに分解できることさえ示せば良いのですから,座標系は何でも良いはずです.基底
を何らかのベクトルに分解できることさえ示せば良いのですから,座標系は何でも良いはずです.基底 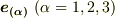 の第
の第 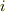 共変成分を
共変成分を 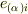 ,第
,第 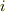 反変成分を
反変成分を  とし,積
とし,積 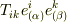 を
を  と書くことにします.これはスカラーになります.
と書くことにします.これはスカラーになります.  や
や 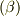 は基底の種類を指定しているだけで,テンソルの添字ではないことに注意して下さい.
は基底の種類を指定しているだけで,テンソルの添字ではないことに注意して下さい. 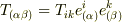 の両辺に共変成分の積
の両辺に共変成分の積 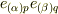 を掛け,
を掛け, 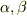 と
と 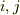 について総和を取ります.(左辺に
について総和を取ります.(左辺に 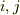 は含まれていないので,
は含まれていないので, 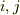 の和は右辺にしか出てきません.)
の和は右辺にしか出てきません.) 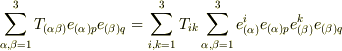 .ここで,基底の積については直交座標を選んだことにより
.ここで,基底の積については直交座標を選んだことにより 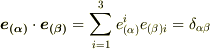 が成り立つことから,
が成り立つことから, 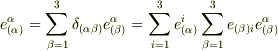 が言えます.(ここの式変形はややトリッキーです.右辺を実際に展開してみればすぐに確認できます.)右辺は計量テンソルを用いて
が言えます.(ここの式変形はややトリッキーです.右辺を実際に展開してみればすぐに確認できます.)右辺は計量テンソルを用いて 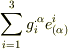 と変形できることから,最初の
と変形できることから,最初の 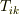 の式は
の式は 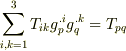 と変形できます.さらに計量テンソルに関して
と変形できます.さらに計量テンソルに関して 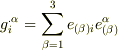 が成り立ちますので,これを代入すると
が成り立ちますので,これを代入すると 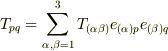 を得ます.これはつまり,
を得ます.これはつまり, 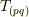 を
を 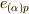 と
と 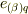 の積で表示する式に他なりませんので定理が示されます.■
の積で表示する式に他なりませんので定理が示されます.■
より一般には,  階のテンソルと
階のテンソルと 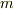 階のテンソルの積は,
階のテンソルの積は, 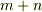 階のテンソルになります.上の定理は,
階のテンソルになります.上の定理は, 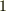 階のテンソルであるベクトルに限ってこの乗法を考えた特別な場合だと言えます.このようなテンソル同士の積を テンソルの直積 と呼びます. テンソルの加法と乗法 でもう一度考えます.
階のテンソルであるベクトルに限ってこの乗法を考えた特別な場合だと言えます.このようなテンソル同士の積を テンソルの直積 と呼びます. テンソルの加法と乗法 でもう一度考えます.
theorem
 階のテンソルと
階のテンソルと 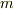 階のテンソルの積は
階のテンソルの積は 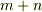 階のテンソルになります.
階のテンソルになります.