テンソル代数
私達は,テンソル積と呼ぶ乗法を導入しました.高校までのベクトル代数では,ベクトルとベクトルの演算に内積  と外積
と外積  しかありませんでしたから,積はいつでもスカラーかベクトルでした.代数的に言えば,ベクトル空間
しかありませんでしたから,積はいつでもスカラーかベクトルでした.代数的に言えば,ベクトル空間 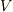 とスカラー
とスカラー 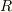 だけで内積と外積の演算は閉じていて,どんなベクトルの演算を考えても
だけで内積と外積の演算は閉じていて,どんなベクトルの演算を考えても 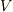 と
と 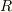 を足した集合
を足した集合 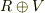 の中で閉じていたということです.これはそれほど難しい話ではありません.
の中で閉じていたということです.これはそれほど難しい話ではありません.
ところが,さきほど導入したテンソル積を考えると,ベクトルとベクトルのテンソル積から二階のテンソルが作れます.
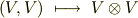
二階のテンソル空間 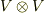 は,ベクトル空間
は,ベクトル空間 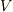 とは異なるベクトル空間であることに注意して下さい.つまり,テンソル積を考えると,ベクトル同士の積から,もとのベクトル空間には収まりきらない積が出て来るということです.更に一般には,
とは異なるベクトル空間であることに注意して下さい.つまり,テンソル積を考えると,ベクトル同士の積から,もとのベクトル空間には収まりきらない積が出て来るということです.更に一般には, 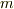 階のテンソルと
階のテンソルと  階のテンソルのテンソル積が
階のテンソルのテンソル積が 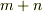 階のテンソルになりました.
階のテンソルになりました.
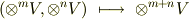
このようにしてテンソル空間の階数は幾らでも上げることが出来ます.ですから,『あらゆるテンソルの演算をカバーする空間』を考える場合,それは次のように全ての階数(無限まで)のテンソル空間を足し合わせたものでなければなりません.
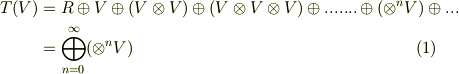
このような空間 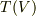 を,
を, 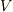 上の テンソル代数 と呼びます.(二行目で,
上の テンソル代数 と呼びます.(二行目で, 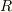 は
は 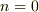 の場合として
の場合として 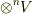 に含めました.)
に含めました.) 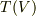 はいわばテンソル計算の数学的な土俵となります.今までの言葉を使えば,『テンソル代数とはテンソル積の定義された無限次元のベクトル空間である』と言えるでしょう.
はいわばテンソル計算の数学的な土俵となります.今までの言葉を使えば,『テンソル代数とはテンソル積の定義された無限次元のベクトル空間である』と言えるでしょう.
| [*] | テンソル代数という名前ですが,これは一種のベクトル空間です.「代数」と聞いて「方程式を計算する数学の分野?」と思ってしまう人は,古典的教養はありますが,現代数学に不慣れな人です.現代の数学では,代数という意味が拡大しており,乗法の定義されたベクトル空間を「代数」( 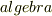 )と呼んでしまうことがしばしばです.最初,言葉で混乱するかも知れませんが徐々に慣れていきましょう. )と呼んでしまうことがしばしばです.最初,言葉で混乱するかも知れませんが徐々に慣れていきましょう. |
テンソル空間の次元
式 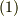 で,
で, 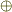 によって結合されている各
によって結合されている各 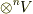 を 直和因子 と呼びます.個々の直和因子は n次のテンソル空間 になっています.
を 直和因子 と呼びます.個々の直和因子は n次のテンソル空間 になっています. 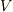 を
を 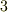 次元のベクトル空間だとすると,
次元のベクトル空間だとすると, 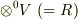 の基底は
の基底は 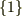 の
の 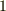 個,
個, 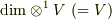 は
は 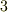 ,
, 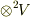 の基底は
の基底は 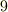 種類あるので
種類あるので 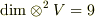 となります.
となります.
一般に, 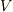 を
を 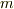 次元のベクトル空間とすれば,次式がなりたちます.
次元のベクトル空間とすれば,次式がなりたちます.
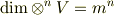
各次元のテンソル空間の次数はこのように有限ですが,テンソル代数 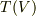 は無限次までのテンソル空間の和集合ですので,結局,
は無限次までのテンソル空間の和集合ですので,結局, 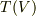 をベクトル空間と見たとき,
をベクトル空間と見たとき, 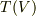 の次元は無限になってしまうわけです.そんなものを考えて何が嬉しいかと言えば,『どのようなテンソルの計算を考えても閉じている空間を考えられた』ことです.テンソル代数は,すべてのテンソルを包含する集合なわけで,どんなテンソルもテンソル代数の元になります.
の次元は無限になってしまうわけです.そんなものを考えて何が嬉しいかと言えば,『どのようなテンソルの計算を考えても閉じている空間を考えられた』ことです.テンソル代数は,すべてのテンソルを包含する集合なわけで,どんなテンソルもテンソル代数の元になります.
テンソル代数の代数構造
テンソル成分の加法と乗法 で考えた演算規則をテンソル代数の視点から考え直すと,同じ直和因子に含まれる二つのテンソルを,やはり同じ直和因子に含まれるテンソルとして表現するのが加法,異なる直和因子( 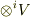 と
と 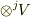 としましょう)に含まれるテンソルを,
としましょう)に含まれるテンソルを, 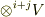 に含まれるテンソルとして表現するのが乗法(テンソル積)だと言えます.
に含まれるテンソルとして表現するのが乗法(テンソル積)だと言えます.
加法と乗法が定義されたので,次にテンソル代数がどのような代数構造を持つのか,具体的には,群なのか,環なのか,体なのかという点に興味が湧いてきます.そもそも,テンソルの計算が閉じている集合が欲しくてテンソル代数なんてものを考えたのです.テンソル代数は,どのような代数構造を持っているのでしょうか?
| [†] | そうは言っても,代数学に不慣れな人は,代数構造になんて何の興味も湧かないかも知れませんね. 群の公理 , 環 , 体 などを参照してみてください.少し数学に馴れてくると,加法と乗法と聞いただけで代数構造が気になるようになります.ちょうど,美味しいラーメンと聞けば,味噌か醤油かトンコツかが自動的に気になるようなものです.(違うかな?)不慣れな読者の方も,これを機会に代数学の美味しさを覚えて頂きたいものです.ヤムヤム... |
テンソルの加法と乗法について,その代数的構造を考えてみましょう. 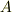 や
や 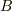 はテンソルだとします.
はテンソルだとします.
【テンソルの加法】
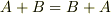 (可換である)
(可換である)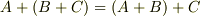 (結合則がなりたつ)
(結合則がなりたつ)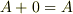 (単位元がある)
(単位元がある)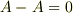 (逆元がある)
(逆元がある)
【テンソル積】
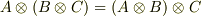 (結合則がなりたつ)
(結合則がなりたつ)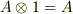 (単位元がある.ただし
(単位元がある.ただし 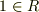 .)
.)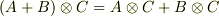 (分配則がなりたつ)
(分配則がなりたつ)
テンソル積は可換ではないこと( 多重線形性とテンソル空間 参照),テンソル積の逆演算は考えていないことに注意しましょう.これらの性質から,テンソル代数は環(より正確には, 単位元を持つ非可換環 )になることが分かります.(よく分からない人は 環 を参照して下さい.)
テンソル代数は乗法の定義された無限次元のベクトル空間で,ベクトル空間 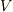 から構成され,環にもなるということでした.私達は,テンソルとテンソルの演算について,非常に一般的な,いわば俯瞰的な立場からその代数的な性質を考えてみました.こんなことを知っていると何かの役にたつかと言えば,すぐにテストの(特に物理や工学の)問題を解くような役には立たないでしょう.しかし『テンソルって一体全体何なんだ?』というような疑問を抱いていた人は,多少頭がすっきりしたのではないでしょうか.(スッキリしたことを望みます.)代数学的な話はこれで一区切りにして,次の記事からはもう少し応用的な話に戻ります.
から構成され,環にもなるということでした.私達は,テンソルとテンソルの演算について,非常に一般的な,いわば俯瞰的な立場からその代数的な性質を考えてみました.こんなことを知っていると何かの役にたつかと言えば,すぐにテストの(特に物理や工学の)問題を解くような役には立たないでしょう.しかし『テンソルって一体全体何なんだ?』というような疑問を抱いていた人は,多少頭がすっきりしたのではないでしょうか.(スッキリしたことを望みます.)代数学的な話はこれで一区切りにして,次の記事からはもう少し応用的な話に戻ります.
| [‡] | いくらなんでも,無限次元のベクトル空間は実際の計算には不便です.そこで,同じ基底の積 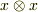 は零になるというような規則を加えると,テンソル空間を有限次元のベクトル空間で収めることが出来るようになり,応用上便利そうです.これを 外積空間 と呼びます.物理のかぎしっぽベクトル解析分野でも,そのうち話題として取り上げる予定です. は零になるというような規則を加えると,テンソル空間を有限次元のベクトル空間で収めることが出来るようになり,応用上便利そうです.これを 外積空間 と呼びます.物理のかぎしっぽベクトル解析分野でも,そのうち話題として取り上げる予定です. |